Pflichtteil - lernen mit Serlo!

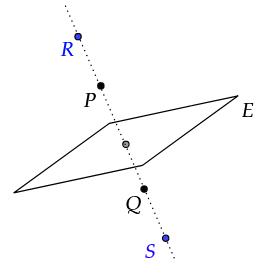
Aufgabe 4

Wird der Punkt $P (1 | 2 | 3)$ an der Ebene $E$ gespiegelt, so ergibt sich der Punkt $Q (7 | 2 | 11)$ .

Bestimmen Sie eine Gleichung von $E$ in Koordinatenform. (3 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Koordinatenform der Ebene (Kurs mit integrierten Aufgaben) (1|5)
Verbindungsvektor $\vec{P Q}$
Der Verbindungsvektor lautet: $\vec{P Q} = \vec{O Q} - \vec{O P} = (\begin{array}{c} 7 - 1 \\ 2 - 2 \\ 11 - 3 \end{array}) = (\begin{array}{c} 6 \\ 0 \\ 8 \end{array})$
Punkt auf der Ebene
Zwischen $P$ und $Q$ liegt ein Punkt $A$ auf der Ebene mit dem Ortsvektor:
$\vec{O A} = \vec{O P} + \frac{1}{2} \cdot \vec{P Q} = (\begin{array}{c} 1 \\ 2 \\ 3 \end{array}) + (\begin{array}{c} 3 \\ 0 \\ 4 \end{array}) = (\begin{array}{c} 4 \\ 2 \\ 7 \end{array})$
Koordinatenform der Ebene
Für die Koordinatenform verwende den gekürzten Normalenvektor $(\begin{array}{c} 3 \\ 0 \\ 4 \end{array})$ .
$E : d$ $=$ $x n_{1} + y n_{2} + z n_{3}$
↓
Einsetzen des Normalenvektors
$d$ $=$ $3 x + 4 z$
↓
$x$ und $z$ von $A$ einsetzen, um $d$ zu bestimmen
$d$ $=$ $3 \cdot 4 + 4 \cdot 7$
$=$ $40$
Die Koordinatenform ist insgesamt: $E : 40 = 3 x + 4 z$
VorsichtAbweichende Ergebnisse
Je nachdem, ob man den Normalenvektor kürzt oder nicht, können äquivalente Koordinatenformen entstehen. Richtig wäre auch:
$E : 80 = 6 x + 8 z$
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Bestimme den Verbindungsvektor $\vec{P Q}$
Berechne die Koordinaten des Punktes, der auf halber Strecke von $P$ nach $Q$ liegt. Dieser Punkt liegt in der Ebene.
Verwende den Verbindungsvektor als Normalenvektor für die Ebene und stelle die Koordinatenform auf.
Auf der Gerade durch $P$ und $Q$ liegen die Punkte $R$ und $S$ symmetrisch bezüglich $E$ . Dabei liegt $R$ bezüglich $E$ auf der gleichen Seite wie $P$ . Der Abstand von $R$ und $S$ ist doppelt so groß wie der Abstand von $P$ und $Q$ .
Bestimmen Sie die Koordinaten von $R$ . (2 BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Punkt an Ebene spiegeln
Koordinaten von $R$
Da die Ebene die Strecken $P Q$ und $R S$ jeweils halbiert und $| R S |$ das Doppelte von $| P Q |$ ist, gilt:
$R$ liegt doppelt so weit von der Ebene entfernt wie $P$ .
Wir gehen den Vektor $\frac{1}{2} \vec{P Q}$ von $P$ aus in Richtung $R$ :
Skizze der Aufgabe
$\vec{O R}$ $=$ $\vec{O P} - \underset{Verbindung von P nach R}{\underset{⏟}{\frac{1}{2} \vec{P Q}}}$
$=$ $(\begin{array}{c} 1 \\ 2 \\ 3 \end{array}) - (\begin{array}{c} 3 \\ 0 \\ 4 \end{array})$
$=$ $(\begin{array}{c} - 2 \\ 2 \\ - 1 \end{array})$
Die Koordinaten sind $R (- 2 | 2 | - 1)$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Hilfreich ist es, eine Skizze anzulegen.
Berechne den Vektor $\vec{O P} - \frac{1}{2} \vec{P Q}$ .

Dieses Werk wurde vom Kultusministerium Niedersachsen zur Verfügung gestellt --- Die Lösungsvorschläge dagegen sind NICHT vom Land Niedersachsen → Was bedeutet das?

$E : d$	$=$	$x n_{1} + y n_{2} + z n_{3}$
	↓	Einsetzen des Normalenvektors
$d$	$=$	$3 x + 4 z$
	↓	$x$ und $z$ von $A$ einsetzen, um $d$ zu bestimmen
$d$	$=$	$3 \cdot 4 + 4 \cdot 7$
	$=$	$40$

$\vec{O R}$	$=$	$\vec{O P} - \underset{Verbindung von P nach R}{\underset{⏟}{\frac{1}{2} \vec{P Q}}}$
	$=$	$(\begin{array}{c} 1 \\ 2 \\ 3 \end{array}) - (\begin{array}{c} 3 \\ 0 \\ 4 \end{array})$
	$=$	$(\begin{array}{c} - 2 \\ 2 \\ - 1 \end{array})$

Aufgabe 4

Verbindungsvektor PQ→

Punkt auf der Ebene

Koordinatenform der Ebene

Hast du eine Frage oder Feedback?

Koordinaten von R

Hast du eine Frage oder Feedback?

Verbindungsvektor $\vec{P Q}$

Koordinaten von $R$