Pflichtteil

🎓 Prüfungsbereich für Niedersachsen

Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

Wichtig: Für die Aufgaben hier gelten andere Nutzungbedingungen.

Aufgaben zur Abiturprüfung eA 2022, Pflichtteil. Zum Download hier.

Aufgabe 1

Für eine Funktion $h$ gilt: $h^{\prime}(x)=x^{2}-2 x-24$ .

Bestimmen Sie die Extremstellen des Graphen von $h$ . (3 BE)

Eine ganzrationale Funktion $f$ hat die Nullstellen 1, 2 und -3.
Für $f$ gilt außerdem: $\lim _{x \rightarrow \infty} f(x) \rightarrow-\infty$ und $\lim _{x \rightarrow-\infty} f(x) \rightarrow-\infty$
Geben Sie eine Funktionsgleichung für $f$ an. (2 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Vielfachheit von Nullstellen
Funktionsterm in Nullstellenform/Produktform
Die Nullstellen können direkt in den Funktionsterm übersetzt werden:
Anpassung des Funktionsterms
Die Funktion verläuft nach der Aufgabenstellung so: Sie kommt von unten und geht nach unten. Das bedeutet:
Der Grad der Funktion ist gerade.
Der Leitkoeffizient hat ein negatives Vorzeichen.
Eine mögliche Lösung wäre also:
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Stelle den Funktionsterm in der Nullstellenform/Produktform auf.
Untersuche die Grenzwerte der Funktion und
passe das Vorzeichen an
passe die Vielfachheit der Nullstellen an

2
Niedersächsisches Kultusministerium (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Kultusministerium Niedersachsen zur Verfügung gestellt --- Die Lösungsvorschläge dagegen sind NICHT vom Land Niedersachsen
Aufgabe 2
Betrachtet werden die in $\mathbb{R}$ definierten
Funktionen $f$ und $F$ , wobei $F$ eine
Stammfunktion von $f$ ist.
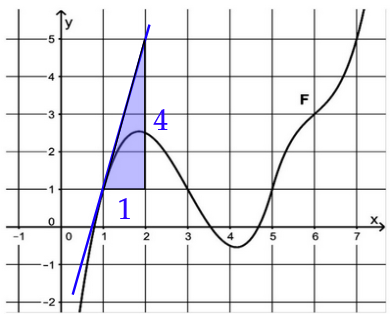
Die Abbildung zeigt den Graphen von $F$ .
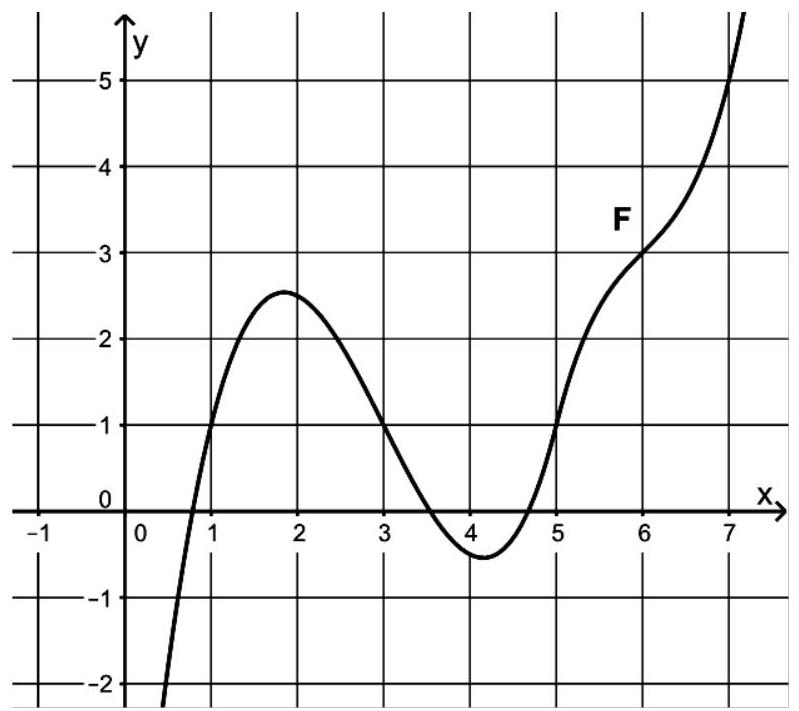
1. Bestimmen Sie den Wert des Integrals $\int_{1}^{7} f(x) d x$ . (2 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Hauptsatz der Differential- und Integralrechnung
  Werte der Stammfunktion
  Die Stammfunktion hat die Funktionswerte:
  $F(7)=5$
  $F(1)=1$
  Wert des Integrals
  Das Integral ist nach dem Hauptsatz der Differential- und Integralrechnung:
  $\displaystyle \int_1^7f(x)dx$ $=$ $\displaystyle F\left(7\right)-F\left(1\right)$
  ↓
  Einsetzen
  $=$ $\displaystyle 5-1$
  $=$ $\displaystyle 4$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Lies die Funktionswerte $F(7)$ und $F(1)$ aus dem Schaubild ab.
  Bestimme den Wert des Integrals.
2. Bestimmen Sie den Funktionswert von $f$ an der Stelle 1.
  Veranschaulichen Sie Ihr Vorgehen in der Abbildung. (3 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Hauptsatz der Differential- und Integralrechnung
  Funktionswert $f(1)$
  Laut dem Hauptsatz der Differential- und Integralrechnung gilt:
  Die Ableitung von $F$ ist die Funktion $f$ .
  Der Funktionswert $f(1)$ ist damit die Steigung, die $F$ an der Stelle $x=1$ hat.
  Mithilfe des Schaubilds gilt: $F'(1)=f(1)=\dfrac41=4$
  Schaubild mit Steigungsdreieck
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Bestimme die Steigung von $F$ an der Stelle $x=1$ .
  Verwende das Schaubild und skizziere ein Steigungsdreieck.

Aufgabe 3

Betrachtet werden die in $\mathbb{R}$ definierten Funktionen $f_{k}$ mit $f_{k}(x)=k \cdot e^{-x}+3$ und $k \neq 0$ .

Zeigen Sie, dass $f_{k}^{\prime}(0)=-k$ gilt. (1 BE)

Bestimmen Sie diejenigen Werte von $k$ , für die die Tangente im Punkt $\left(0 \mid f_{k}(0)\right)$ an den Graphen von $f_{k}$ eine positive Steigung hat und ihre Schnittstelle mit der $x$ -Achse größer als $\frac{1}{2}$ ist. (4 BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Tangente an Graph

Tangentengleichung

Allgemein hat die Tangente im Punkt $(0\mid f_k(0))$ den Funktionsterm:

Tangentenformel
	↓
$\displaystyle f_k\left(x\right)$	$=$	$\displaystyle f_k'\left(x\right)\cdot\left(x-x_0\right)+f_k\left(x_0\right)$
	↓	$x_0=0$ einsetzen
	$=$	$\displaystyle f_k'\left(0\right)\cdot\left(x-0\right)+f_k\left(0\right)$
	↓	Verwende $f_k'(0)=-k$ (letzte Teilaufgabe)
	$=$	$\displaystyle -k\cdot x+f_k\left(0\right)$
	↓	Berechne $f_k(0)=k\cdot e^0+3=k+3$
	$=$	$\displaystyle \underbrace{-k}_{\text{Steigung}}\cdot x+\underbrace{k+3}_{\text{y-Achsenabschnitt}}$

Damit die Tangente eine positive Steigung hat, muss $k<0$ sein.

Nullstelle der Tangente

Beachte nun zusätzlich die Lage der Nullstelle

$\displaystyle f_t\left(x\right)$	$=$	$\displaystyle -k\cdot x+k+3$
	↓	An der Nullstelle gilt $f_t(x)=0$
$\displaystyle 0$	$=$	$\displaystyle -k\cdot x+k+3$	$\displaystyle +kx$
$\displaystyle kx$	$=$	$\displaystyle k+3$	$\displaystyle :k$
$\displaystyle x$	$=$	$\displaystyle \dfrac{k+3}{k}$
	↓	$x$ soll größer sein als $\frac12$
$\displaystyle \dfrac12$	$<$	$\displaystyle \dfrac{k+3}{k}$	$\displaystyle \cdot k$
	↓	Das Vorzeichen muss sich drehen, weil $k$ negativ ist.
$\displaystyle \dfrac12\cdot k$	$>$	$\displaystyle k+3$	$\displaystyle -k$
$\displaystyle -\dfrac12\cdot k$	$>$	$\displaystyle 3$	$\displaystyle \cdot (-1)$
	↓	Das Vorzeichen dreht sich.
$\displaystyle \dfrac12\cdot k$	$<$	$\displaystyle -3$	$\displaystyle \cdot 2$
$\displaystyle k$	$<$	$\displaystyle -6$

Für $k<-6$ hat $f_t(x)$ positive Steigung und gleichzeitig eine Nullstelle mit $x>\dfrac12$ .

Hast du eine Frage oder Feedback?

Kommentiere hier 👉

Aufgabe 4

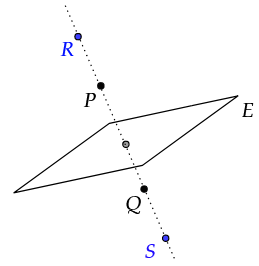
Wird der Punkt $P(1|2| 3)$ an der Ebene $E$ gespiegelt, so ergibt sich der Punkt $Q(7|2| 11)$ .

Bestimmen Sie eine Gleichung von $E$ in Koordinatenform. (3 BE)

Auf der Gerade durch $P$ und $Q$ liegen die Punkte $R$ und $S$ symmetrisch bezüglich $E$ . Dabei liegt $R$ bezüglich $E$ auf der gleichen Seite wie $P$ . Der Abstand von $R$ und $S$ ist doppelt so groß wie der Abstand von $P$ und $Q$ .

Bestimmen Sie die Koordinaten von $R$ . (2 BE)

5
Niedersächsisches Kultusministerium (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Kultusministerium Niedersachsen zur Verfügung gestellt --- Die Lösungsvorschläge dagegen sind NICHT vom Land Niedersachsen
Aufgabe 5
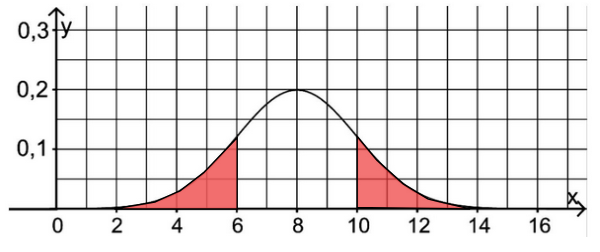
Die Abbildung zeigt den Graphen der Dichtefunktion der normalverteilten Zufallsgröße $A$ .
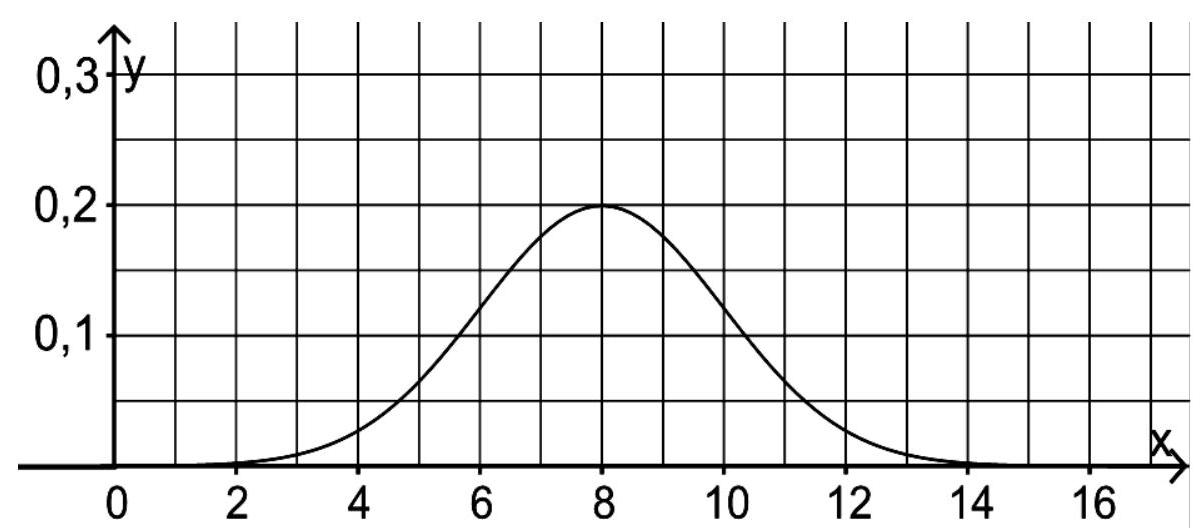
1. Die Wahrscheinlichkeit dafür, dass $A$ einen Wert aus dem Intervall $[6 ; 10]$ annimmt, beträgt etwa $68 \%$ .
  Berechnen Sie die Wahrscheinlichkeit dafür, dass $A$ einen Wert annimmt, der größer als 10 ist. (2 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Normalverteilung
  Wahrscheinlichkeit für $A$ größer als $10$
  Wenn $P(6\le A\le10)=68~\%$ beträgt, dann ist:
  $P(A\le6)+P(A\ge10)=32~\%$
  Denn insgesamt muss die Wahrscheinlichkeit $100~\%$ betragen.
  Skizze der Verteilung
  Da die Verteilung symmetrisch um den Erwartungswert $\mu=8$ ist, teilen sich $P(A\le6)$ und $P(A\ge10)$ die gleiche Wahrscheinlichkeit.
  $\Rightarrow P(A\ge10)=16~\%$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Bestimme die Wahrscheinlichkeit, dass $A$ einen Wert außerhalb $[6;10]$ annimmt.
  Berechne die Wahrscheinlichkeit, dass $A$ größer 10 ist.
  Verwende hierzu, dass die Normalverteilung symmetrisch ist.
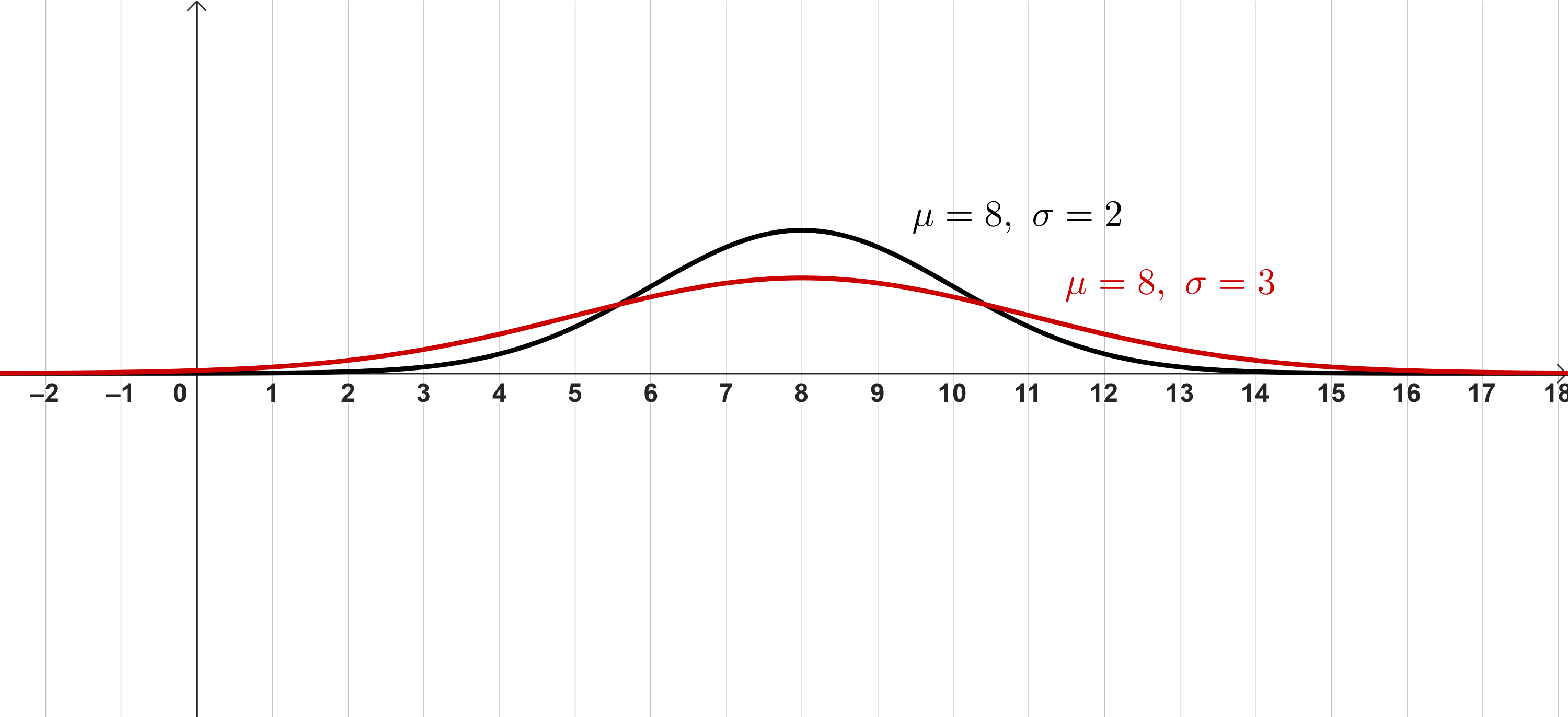
2. Die Zufallsgröße $B$ ist ebenfalls normalverteilt. Der Erwartungswert von $B$ ist ebenso groß wie der Erwartungswert von $A$ , die Standardabweichung von $B$ ist größer als die Standardabweichung von $A$ .
  Skizzieren Sie in der Abbildung einen möglichen Graphen der Dichtefunktion von $B$ .
  (3 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Normalverteilung
  Beispiel einer breiteren Verteilung
  Beispiellösung mit $\sigma=3$ .
  Jede Verteilung mit $\sigma>2$ wäre richtig.
  Veranschaulichung
  Verändere $\sigma$ . Hier kannst du dir verschiedene Verteilungen anzeigen lassen.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Skizziere eine Normalverteilung mit größerer Breite.
  Achte darauf, dass die Verteilung aufgrund der größeren Breite flacher in der Mitte ist.

Aufgabe 6

Für ein Spiel wird ein Behälter mit 100 Kugeln gefüllt. Dafür stehen rote und blaue Kugeln zur Verfügung. Vor jedem Spiel legt die spielende Person die Anzahl der blauen Kugeln im Behälter fest. Anschließend wird dem Behälter eine Kugel zufällig entnommen. Ist diese Kugel rot, so wird der spielenden Person die festgelegte Anzahl blauer Kugeln in Cent ausgezahlt. Ist die Kugel blau, so beträgt die Auszahlung 10 Cent.

Ermitteln Sie, wie die spielende Person die Anzahl blauer Kugeln für ein Spiel festlegen muss, damit der Erwartungswert der Auszahlung möglichst groß ist. (5 BE)

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

$\displaystyle h'\left(x\right)$	$=$	$\displaystyle x^2-2x-24$
	↓	0 setzen
$\displaystyle 0$	$=$	$\displaystyle x^2-2x-24$
	↓	Lösen mit $pq$ -Formel.
$\displaystyle x_{1{,}2}$	$=$	$\displaystyle -\frac{p}{2}\pm\sqrt{\left(\frac{p}{2}\right)^2-q}$
	↓	$p=-2,~q=-24$
	$=$	$\displaystyle -\frac{\left(-2\right)}{2}\pm\sqrt{\left(\frac{-2}{2}\right)^2-\left(-24\right)}$
	↓	Zusammenfassen
	$=$	$\displaystyle 1\pm\sqrt{1+24}$
	$=$	$\displaystyle 1\pm5$
$\displaystyle x_1$	$=$	$\displaystyle 6$
$\displaystyle x_2$	$=$	$\displaystyle -4$

$\displaystyle E:\ d$	$=$	$\displaystyle xn_1+yn_2+zn_3$
	↓	Einsetzen des Normalenvektors
$\displaystyle d$	$=$	$\displaystyle 3x+4z$
	↓	$x$ und $z$ von $A$ einsetzen, um $d$ zu bestimmen
$\displaystyle d$	$=$	$\displaystyle 3\cdot4+4\cdot7$
	$=$	$\displaystyle 40$

$\displaystyle \overrightarrow{OR}$	$=$	$\displaystyle \overrightarrow{OP}-\underbrace{\frac12\overrightarrow{PQ}}_{\text{Verbindung von P nach R}}$
	$=$	$\displaystyle \begin{pmatrix}1\\2\\3\end{pmatrix}-\begin{pmatrix}3\\0\\4\end{pmatrix}$
	$=$	$\displaystyle \begin{pmatrix}-2\\2\\-1\end{pmatrix}$

$\displaystyle E\left(x\right)$	$=$	$\displaystyle \frac{100-x}{100}\cdot x+\frac{x}{100}\cdot10$
	↓	Suche Maximum, zum Beispiel durch Ableiten
$\displaystyle E'\left(x\right)$	$=$	$\displaystyle \frac{100}{100}-\frac{1}{100}2x+\frac{10}{100}$
	↓	Zusammenfassen und 0 setzen
$\displaystyle 0$	$=$	$\displaystyle 1{,}1-\frac{2}{100}x$	$\displaystyle +\frac{2}{100}x$
$\displaystyle \frac{2}{100}x$	$=$	$\displaystyle 1{,}1$	$\displaystyle \cdot100$
$\displaystyle 2x$	$=$	$\displaystyle 110$	$\displaystyle :2$
$\displaystyle x$	$=$	$\displaystyle 55$

Pflichtteil

Aufgabe 1

Ableitung $0$ setzen und Extremstellen bestimmen

Hast du eine Frage oder Feedback?

Funktionsterm in Nullstellenform/Produktform

Anpassung des Funktionsterms

Hast du eine Frage oder Feedback?

Aufgabe 2

Werte der Stammfunktion

Wert des Integrals

Hast du eine Frage oder Feedback?

Funktionswert $f(1)$

Hast du eine Frage oder Feedback?

Aufgabe 3

Ableitung bestimmen

$f'_k(0)$ bestimmen

Hast du eine Frage oder Feedback?

Tangentengleichung

Nullstelle der Tangente

Hast du eine Frage oder Feedback?

Aufgabe 4

Verbindungsvektor $\overrightarrow{PQ}$

Punkt auf der Ebene

Koordinatenform der Ebene

Hast du eine Frage oder Feedback?

Koordinaten von $R$

Hast du eine Frage oder Feedback?

Aufgabe 5

Wahrscheinlichkeit für $A$ größer als $10$

Hast du eine Frage oder Feedback?

Beispiel einer breiteren Verteilung

Veranschaulichung

Hast du eine Frage oder Feedback?

Aufgabe 6

Erwartungswert

Maximum des Erwartungswerts

$\displaystyle \int_1^7f(x)dx$	$=$	$\displaystyle F\left(7\right)-F\left(1\right)$
	↓	Einsetzen
	$=$	$\displaystyle 5-1$
	$=$	$\displaystyle 4$

$\displaystyle f_k\left(x\right)$	$=$	$\displaystyle k\cdot e^{-x}+3$
	↓	Kettenregel mit $e^{-x}$
$\displaystyle f_k'\left(x\right)$	$=$	$\displaystyle k\cdot\left(-1\right)\cdot e^{-x}$
	↓	Vereinfachen
	$=$	$\displaystyle -k\cdot e^{-x}$

$x=0$ einsetzen in Ableitung
	↓
$\displaystyle f_k'\left(0\right)$	$=$	$\displaystyle -k\cdot e^{-0}$
	↓	$e^0=1$
	$=$	$\displaystyle -k\cdot1$
	$=$	$\displaystyle -k$

$\displaystyle E\left(x\right)$	$=$	$\displaystyle P\left(rot\right)\cdot\text{Auszahlung}_{rot}+P\left(blau\right)\cdot\text{Auszahlung}_{blau}$
	↓	Einsetzen
	$=$	$\displaystyle \frac{100-x}{100}\cdot x+\frac{x}{100}\cdot10$

Pflichtteil

Aufgabe 1

Ableitung 000 setzen und Extremstellen bestimmen

Hast du eine Frage oder Feedback?

Funktionsterm in Nullstellenform/Produktform

Anpassung des Funktionsterms

Hast du eine Frage oder Feedback?

Aufgabe 2

Werte der Stammfunktion

Wert des Integrals

Hast du eine Frage oder Feedback?

Funktionswert f(1)f(1)f(1)

Hast du eine Frage oder Feedback?

Aufgabe 3

Ableitung bestimmen

fk′(0)f'_k(0)fk′​(0) bestimmen

Hast du eine Frage oder Feedback?

Tangentengleichung

Nullstelle der Tangente

Hast du eine Frage oder Feedback?

Aufgabe 4

Verbindungsvektor PQ→\overrightarrow{PQ}PQ​

Punkt auf der Ebene

Koordinatenform der Ebene

Hast du eine Frage oder Feedback?

Koordinaten von RRR

Hast du eine Frage oder Feedback?

Aufgabe 5

Wahrscheinlichkeit für AAA größer als 101010

Hast du eine Frage oder Feedback?

Beispiel einer breiteren Verteilung

Veranschaulichung

Hast du eine Frage oder Feedback?

Aufgabe 6

Erwartungswert

Maximum des Erwartungswerts

Ableitung $0$ setzen und Extremstellen bestimmen

Funktionswert $f(1)$

$f'_k(0)$ bestimmen

Verbindungsvektor $\overrightarrow{PQ}$

Koordinaten von $R$

Wahrscheinlichkeit für $A$ größer als $10$