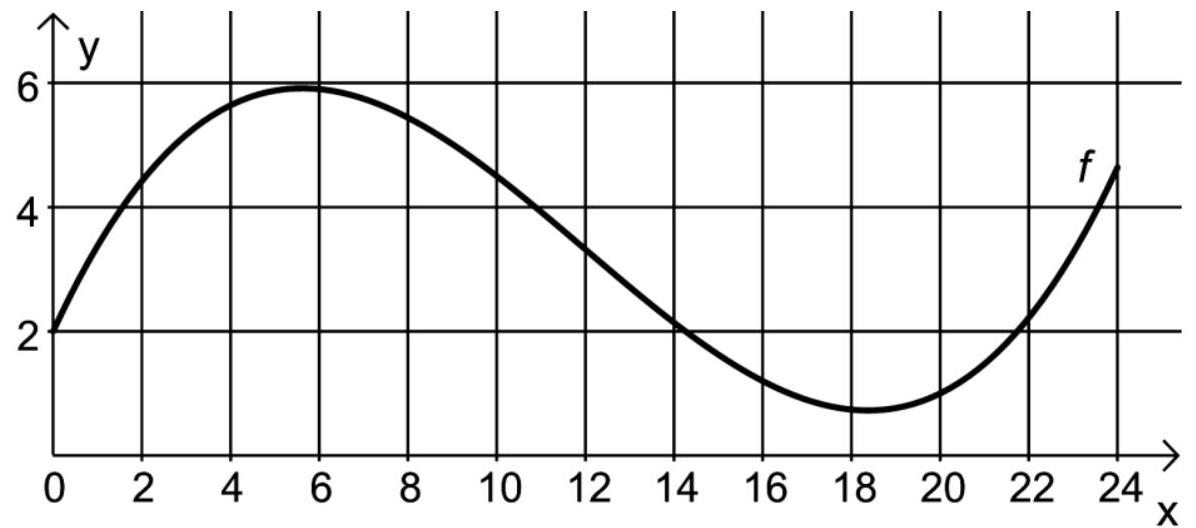
Geben Sie $f(2)$ an und interpretieren Sie den Wert im Sachzusammenhang

Es ist $f(2)=0{,}005\cdot 2^{3}-0{,}18 \cdot 2^{2}+1{,}55 \cdot 2+2=4{,}42$

Die Zuflussrate zwei Stunden nach Beobachtungsbeginn beträgt etwa $4400\;\frac{\mathrm{m}^{3}}{\mathrm{h}}$.

Begründen Sie mithilfe des Graphen von $f$, dass der Wasserstand im Stausee ständig ansteigt

Der Graph von $f$ verläuft im Beobachtungszeitraum vollständig oberhalb der

x-Achse. Deshalb nimmt die Wassermenge ständig zu und der Wasserspiegel steigt an.

Die Länge des Zeitraums, in dem die Zuflussrate geringer als $1000 \frac{\mathrm{m}^{3}}{\mathrm{h}}$

Berechne $f(x)=1$.

Für $0 \leq x \leq 24$ liefert der GTR-Rechner die Lösungen $x_1\approx16{,}602325...$ und $x_2=20$.

Dann ist $x_2-x_1\approx3{,}4$.

Für etwa $3{,}4 \;\mathrm{h}$ ist die Zuflussrate geringer als $1000 \frac{\mathrm{m}^{3}}{\mathrm{h}}$.

Berechnen Sie die maximale Zuflussrate im Beobachtungszeitraum

Die maximale Zuflussrate liegt dort, wo der Graph von $f$ einen Hochpunkt hat.

Das Funktionsmaximum ergibt sich mithilfe des Graphens von $f$ im betrachteten Intervall an der Stelle $x_M\approx5{,}622957...$.

Der Funktionswert an der Stelle $x_M$ ist $y_M\approx5{,}913330...$.

Damit beträgt die maximale Zuflussrate etwa $5900\;\frac{\mathrm{m}^{3}}{\mathrm{h}}$.

Die Zeitpunkte, an denen die Zuflussrate am stärksten abnimmt

Der Graph der Ableitungsfunktion beschreibt die Änderung der Zuflussrate.

Der Graph ist eine nach oben geöffnete Parabel $f'(x)=\dfrac{3}{200}\cdot x^2-\dfrac{9}{25}\cdot x+\dfrac{31}{20}$.

Der GTR-Rechner liefert mit $\dfrac{d}{dx}\left(f'(x)\right)=0$ den Wert $x=12$.

Die Parabel hat einen Tiefpunkt an der Stelle $12$.

Also nimmt die Zuflussrate nach $12\;\text{h}$ am stärksten ab.

Die Zeitpunkte, an denen die Zuflussrate am stärksten zunimmt

Sie nimmt zu Beobachtungsbeginn und nach $24\;\text{h}$ am stärksten zu.

Gibt es eine Zuflussrate, die sich eine Stunde später verdoppelt hat?

Löse die Gleichung: $2\cdot f(x)=f(x+1)$:

Der GTR-Rechner liefert als Lösung nur den Wert $x\approx-0{,}319242...$,

Die Lösung $x\approx -0{,}32$ liegt außerhalb des Definitionsbereiches.

Somit gibt es im Bereich $0 \leq x \leq 23$ keine Lösung für die Gleichung $2\cdot f(x)=f(x+1)$.

Es gibt die gesuchte Zuflussrate nicht.

Der Anstieg der Wasserhöhe innerhalb der 24 Stunden

Berechne das Integral:

$\displaystyle\int_0^{24}f(x)\;dx\approx 79{,}68$

Innerhalb von $24$ Stunden nimmt das Wasservolumen um rund $79680\;\text{m}^3$ zu.

Das Volumen des Stausees ändert sich in dieser Zeit um $1000\;\text{m} \cdot 200\;\text{m} \cdot h$, wobei $h$ die Änderung der Wasserhöhe ist.

$\Rightarrow\;h=\dfrac{79680\;\text{m}^3}{1000\;\text{m} \cdot 200\;\text{m}}\approx 0{,}4\;\text{m}$

Die Wasserhöhe steigt um etwa $0{,}4\;\text{m}$.

Berechnen Sie den Zeitpunkt $t$

Löse die Gleichung:

$\displaystyle\int_0^{t}f(x)\;dx=\displaystyle\int_t^{t+3}f(x)\;dx$

Der GTR-Rechner liefert als Lösung $t\approx 4{,}113869...$.

Im Bereich $0 \leq x \leq 24$ liegt die Lösung $t\approx 4{,}1$.

Von Beobachtungsbeginn bis zum Zeitpunkt $4{,}1 \;\text{h}$ ist eine bestimmte Wassermenge zugeflossen. In den folgenden drei Stunden fließt noch einmal genauso viel Wasser dazu.

Bestimmen Sie die Abflussrate des Stausees so, dass sich $24$ Stunden nach Beobachtungsbeginn genauso viel Wasser im Stausee befindet wie zu Beobachtungsbeginn

$6$ Stunden nach Beobachtungsbeginn wird der Ablauf geöffnet.

$\Rightarrow\;$Es bleiben $18$ Stunden, in denen die Gesamttagesmenge abfließen kann.

$\text{Abflussrate}=\dfrac{79680\;\text{m}^3}{18\;\text{h} }\approx 4427\;\dfrac{\text{m}^3}{\text{h}}$

Die Abflussrate beträgt rund $4400\;\dfrac{\text{m}^3}{\text{h}}$.

Begründen Sie auch mithilfe einer Skizze und ohne Rechnung, dass etwa zum Zeitpunkt $14{,}3 \;\text{h}$ die Wassermenge im Stausee maximal ist

Der Wasserablauf wird zu Beobachtungsbeginn mit einer Abflussrate von $2000\; \frac{\mathrm{m}^{3}}{\mathrm{h}}$ geöffnet. In der Skizze beschreibt die Gerade $g$ die Abflussrate.

Von Beobachtungsbeginn bis etwa $14{,}3\;\text{h}$ und von etwa $21{,}7\;\text{h}$ bis $24\;\text{h}$ verläuft der Graph von $f$ oberhalb von $g$ und die Wassermenge im Stausee nimmt zu.

Von ungefähr $14{,}3\;\text{h}$ bis $21{,}7 \;\text{h}$ verläuft $g$ oberhalb des Graphen von $f$ und die Wassermenge nimmt ab.

Der Inhalt der Fläche zwischen dem Graphen von $f$ und $g$ ist ein Maß für die Veränderung der Wassermenge.

In der Abbildung erkennt man, dass der Flächeninhalt von $A_1$ größer ist als der von $A_2$, d.h. von ungefähr $14{,}3\;\text{h}$ bis $24 \;\text{h}$ nimmt insgesamt die Wassermenge im Stausee ab.

Somit ist die Wassermenge nach etwa $14{,}3 \;\text{h}$ maximal.