Löse die folgenden Gleichungssysteme zunächst graphisch und dann rechnerisch. Gib dein Ergebnis in das Eingabefeld ein.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Lineare Gleichunssysteme
Graphisches Lösen
Um das Gleichungssystem graphisch lösen zu können, kannst du die einzelnen Geichungen nach auflösen und in ein Koordinatensystem einzeichnen. Anschließend brauchst du nur noch die Koordinaten des Schnittpunktes beider Geraden abzulesen.

Der Schnittpunkt liegt bei und .
Rechnerisches Lösen
In diesem Fall bietet sich das Gleichsetzungsverfahren an, da du zum graphischen Lösen bereits beide Gleichungen nach aufgelöst hast.
Setze und gleich und löse nach auf.
Setze den erhaltenen Wert für in eine der Gleichungen ein, z.B in .
Antwort: Die Lösung ist und .
Hast du eine Frage oder Feedback?
Graphisches Lösen: Löse beide Gleichungen nach y auf, und zeichne die Graphen in ein Koordinatensystem.
Rechnerisches Lösen: Verwende das Gleichsetzungsverfahren.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Lineare Gleichungssysteme
Graphisches Lösen
Um das Gleichungssystem graphisch lösen zu können, kannst du die einzelnen Gleichungen nach auflösen und in ein Koordinatensystem einzeichnen. Anschließend brauchst du nur noch die Koordinaten des Schnittpunktes beider Geraden abzulesen.
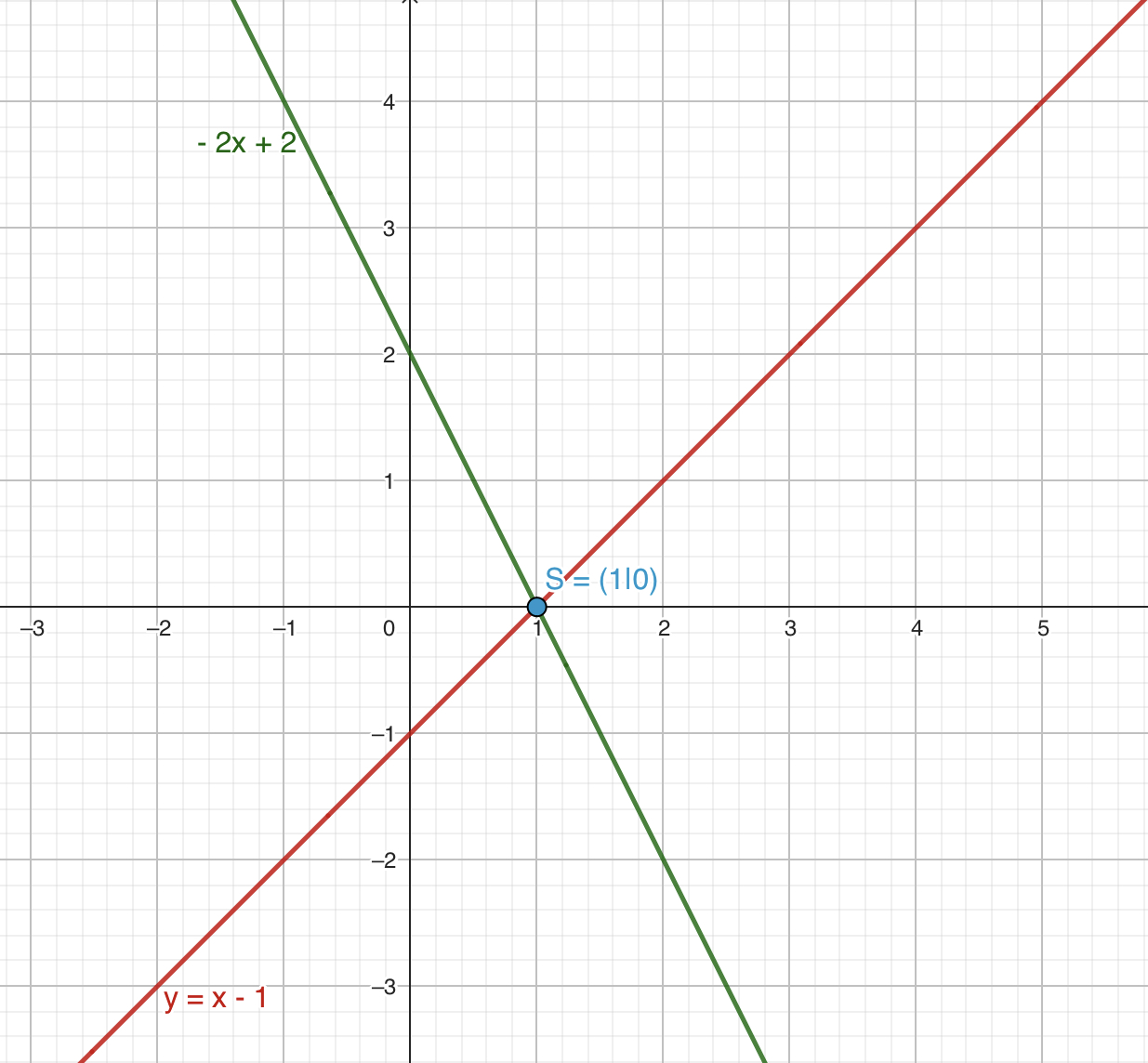
Der Schnittpunkt liegt bei und .
Rechnerisches Lösen
In diesem Fall bietet sich das Gleichsetzungsverfahren an, da du zum graphischen Lösen bereits beide Gleichungen nach aufgelöst hast.
Setze und gleich und löse nach auf.
Setze den erhaltenen Wert für in eine der Gleichungen ein, z.B in .
Antwort: Die Lösung ist und .
Hast du eine Frage oder Feedback?
Graphisches Lösen: Löse beide Gleichungen nach y auf, und zeichne die Graphen in ein Koordinatensystem.
Rechnerisches Lösen: Verwende das Gleichsetzungsverfahren.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Lineare Gleichungssysteme
Graphisches Lösen
Um das Gleichungssystem graphisch lösen zu können, kannst du die einzelnen Geichungen nach auflösen und in ein Koordinatensystem einzeichnen. Anschließend brauchst du nur noch die Koordinaten des Schnittpunktes beider Geraden abzulesen.
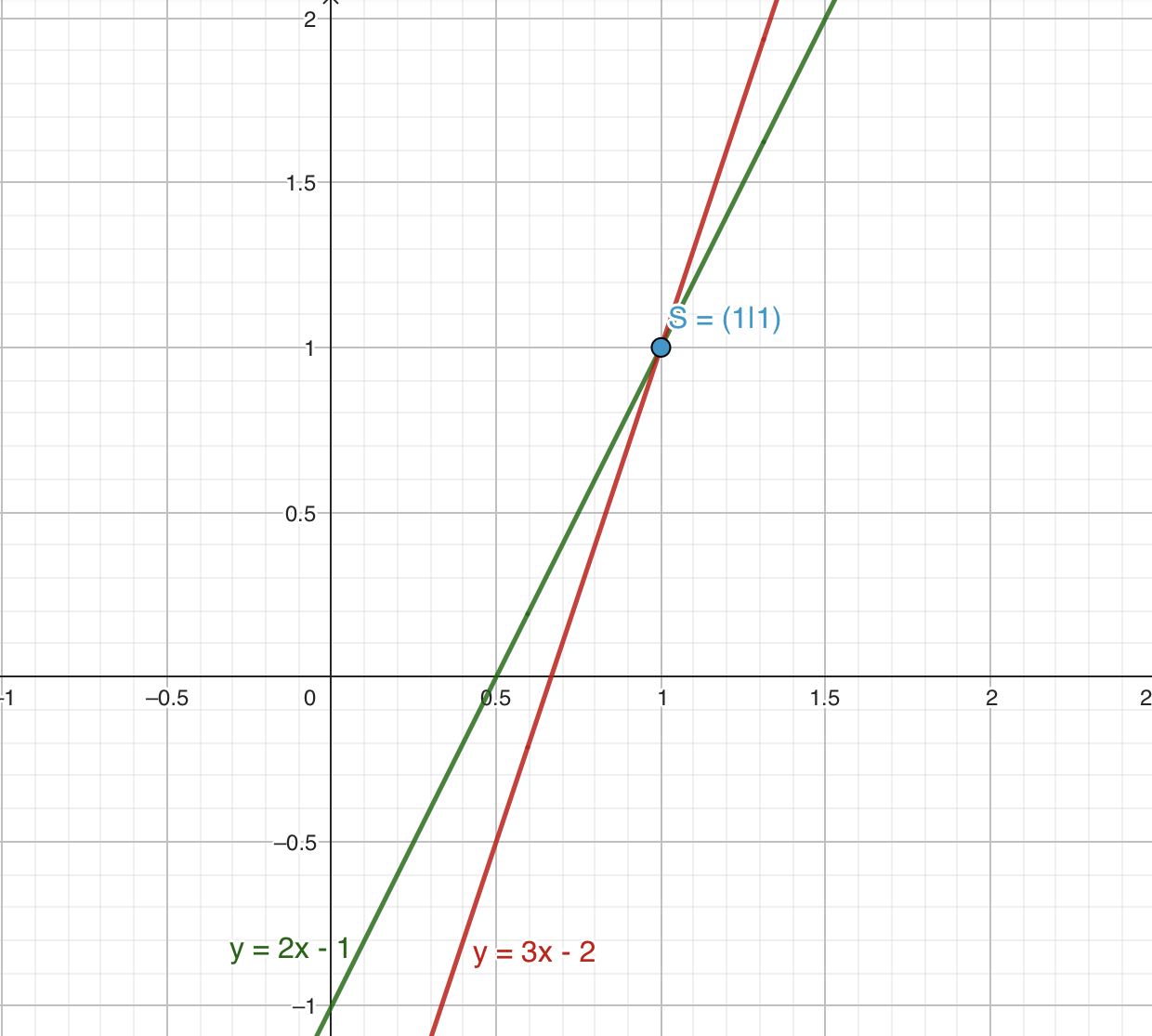
Der Schnittpunkt liegt bei und .
Rechnerisches Lösen
In diesem Fall bietet sich das Gleichsetzungsverfahren an, da du zum graphischen Lösen bereits beide Gleichungen nach aufgelöst hast.
Setze und gleich und löse nach auf.
Setze den erhaltenen Wert für in eine der Gleichungen ein, z.B in .
Antwort: Die Lösung ist und .
Hast du eine Frage oder Feedback?
Graphisches Lösen: Löse beide Gleichungen nach y auf, und zeichne die Graphen in ein Koordinatensystem.
Rechnerisches Lösen: Verwende das Gleichsetzungsverfahren.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?
