test
- 1
Teste dein Wissen! Mit welchem Verfahren ist es sinnvoll, die folgenden Gleichungssysteme zu lösen?
- 2
Wie lassen sich die Gleichungssysteme am besten lösen?
a) Ordne die Gleichungssysteme dem am besten geeigneten Verfahren zu.
b)-h) Löse nun die Gleichungssysteme mit den gewählten Verfahren.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Lineare Gleichungssysteme
Einsetzungsverfahren: Eine Gleichung lässt sich leicht nach einer Variablen auflösen.
Gleichsetzungsverfahren: Beide Gleichungen lassen sich leicht nach der gleichen Variable auflösen.
Additionsverfahren: Wenn man die beiden Gleichungen addiert/subtrahiert, fällt eine Variable weg.
Hast du eine Frage oder Feedback?
Verwende das Einsetzungsverfahren, wenn sich eine Gleichung leicht nach einer Variablen auflösen lässt.
Verwende das Gleichsetzungsverfahren, wenn sich beide Gleichungen leicht nach der gleichen Variablen auflösen lassen.
Verwende das Additionsverfahren, wenn man beide Gleichungen addieren/subtrahieren kann und dadurch eine Variable wegfällt.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Einsetzungsverfahren
Hier bietet sich das Einsetzungsverfahren an, weil schon nach aufgelöst ist.
Wir können also direkt in einsetzen:
Jetzt setzen wir in ein:
Antwort: Die Lösung ist also und .
Hast du eine Frage oder Feedback?
Löse das Gleichungssystem mit dem Einsetzungsverfahren.
Setze in ein.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Gleichsetzungsverfahren
Hier bietet sich das Gleichsetzungsverfahren an, weil beide Gleichungen bereits nach aufgelöst sind. Man kann also direkt und gleichsetzen:
Jetzt können wir in eine der beiden Gleichungen einsetzen. Welche man wählt ist egal.
Wir setzen in ein:
Antwort: Die Lösung ist also und .
Hast du eine Frage oder Feedback?
Löse das Gleichungssystem mit dem Gleichsetzungsverfahren.
Setze
Für diese Aufgabe benötigst Du folgendes Grundwissen: Additionsverfahren
In diesem Fall bietet sich das Additionsverfahren an, weil in beiden Gleichungen vorkommt.
Wir rechnen also :
Jetzt können wir nach auflösen:
Jetzt können wir in oder in einsetzen. Welche Gleichung man wählt ist egal. Wir setzen in ein und erhalten:
Antwort: Die Lösung ist und .
Hast du eine Frage oder Feedback?
Löse das Gleichungssystem mit dem Additionsverfahren.
Rechne .
Für diese Aufgabe benötigst Du folgendes Grundwissen: Einsetzungsverfahren
In diesem Fall ist das Einsetzungsverfahren sinnvoll, da die zweite Gleichung bereits nach einer Variablen aufgelöst ist. Setze also in ein:
Löse nach auf.
Nun kannst du in einsetzen und nach auflösen.
Antwort: Die Lösung ist x = 3 und y = 2.
Hast du eine Frage oder Feedback?
Löse das Gleichungssystem mit dem Einsetzungsverfahren.
Setze in ein.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Additionsverfahren
In diesem Fall bietet sich das Additionsverfahren an, weil in beiden Gleichungen vorkommt.
Wir rechnen also :
Jetzt können wir nach auflösen:
Jetzt können wir in oder in einsetzen. Welche Gleichung man wählt ist egal. Wir setzen in ein und erhalten:
Antwort: Die Lösung ist x = 0 und y = 1.
Hast du eine Frage oder Feedback?
Löse das Gleichungssystem mit dem Additionsverfahren.
Rechne .
Für diese Aufgabe benötigst Du folgendes Grundwissen: Einsetzungsverfahren
Hier bietet sich das Einsetzungsverfahren an, weil man leicht nach einer Variable auflösen kann.
Wir lösen nach auf:
Jetzt können wir in einsetzen:
Jetzt setzen wir in ein:
Antwort: Die Lösung ist also und .
Hast du eine Frage oder Feedback?
Löse das Gleichungssystem mit dem Einsetzungsverfahren.
Löse nach auf und setze dann in ein.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Gleichsetzungsverfahren
Hier bietet sich das Gleichsetzungsverfahren an, weil nach aufgelöst ist. kann man leicht auch nach auflösen:
Jetzt setzen wir die beiden Gleichungen gleich:
Jetzt können wir in eine der beiden Gleichungen einsetzen. Welche man wählt ist egal.
Wir setzen in ein:
Antwort: Die Lösung ist also und .
Hast du eine Frage oder Feedback?
Löse das Gleichungssystem mit dem Gleichsetzungsverfahren.
Löse nach auf und setze dann und gleich.
- 3
Bestimme die Lösung der Gleichungssysteme. Schreibe die Lösung in die Eingabefelder.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Einsetzungsverfahren
In diesem Fall ist das Einsetzungsverfahren sinnvoll, da die zweite Gleichung bereits nach einer Variablen aufgelöst ist. Setze also in ein:
Löse nach auf.
Nun kannst du in einsetzen und nach auflösen.
Antwort: Die Lösung ist x = 3 und y = 2.
Hast du eine Frage oder Feedback?
Löse das Gleichungssystem mit dem Einsetzungsverfahren.
Setze in ein.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Additionsverfahren
In diesem Fall bietet sich das Additionsverfahren an, weil in beiden Gleichungen vorkommt.
Wir rechnen also :
Jetzt können wir nach auflösen:
Jetzt können wir in oder in einsetzen. Welche Gleichung man wählt ist egal. Wir setzen in ein und erhalten:
Antwort: Die Lösung ist x = 0 und y = 1.
Hast du eine Frage oder Feedback?
Löse das Gleichungssystem mit dem Additionsverfahren.
Rechne .
Für diese Aufgabe benötigst Du folgendes Grundwissen: Einsetzungsverfahren
Hier bietet sich das Einsetzungsverfahren an, weil man leicht nach einer Variable auflösen kann.
Wir lösen nach auf:
Jetzt können wir in einsetzen:
Jetzt setzen wir in ein:
Antwort: Die Lösung ist also und .
Hast du eine Frage oder Feedback?
Löse das Gleichungssystem mit dem Einsetzungsverfahren.
Löse nach auf und setze dann in ein.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Gleichsetzungsverfahren
Hier bietet sich das Gleichsetzungsverfahren an, weil nach aufgelöst ist. kann man leicht auch nach auflösen:
Jetzt setzen wir die beiden Gleichungen gleich:
Jetzt können wir in eine der beiden Gleichungen einsetzen. Welche man wählt ist egal.
Wir setzen in ein:
Antwort: Die Lösung ist also und .
Hast du eine Frage oder Feedback?
Löse das Gleichungssystem mit dem Gleichsetzungsverfahren.
Löse nach auf und setze dann und gleich.
- 4
Löse die folgenden Gleichungssysteme zunächst graphisch und dann rechnerisch. Gib dein Ergebnis in das Eingabefeld ein.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Lineare Gleichunssysteme
Graphisches Lösen
Um das Gleichungssystem graphisch lösen zu können, kannst du die einzelnen Geichungen nach auflösen und in ein Koordinatensystem einzeichnen. Anschließend brauchst du nur noch die Koordinaten des Schnittpunktes beider Geraden abzulesen.

Der Schnittpunkt liegt bei und .
Rechnerisches Lösen
In diesem Fall bietet sich das Gleichsetzungsverfahren an, da du zum graphischen Lösen bereits beide Gleichungen nach aufgelöst hast.
Setze und gleich und löse nach auf.
Setze den erhaltenen Wert für in eine der Gleichungen ein, z.B in .
Antwort: Die Lösung ist und .
Hast du eine Frage oder Feedback?
Graphisches Lösen: Löse beide Gleichungen nach y auf, und zeichne die Graphen in ein Koordinatensystem.
Rechnerisches Lösen: Verwende das Gleichsetzungsverfahren.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Lineare Gleichungssysteme
Graphisches Lösen
Um das Gleichungssystem graphisch lösen zu können, kannst du die einzelnen Gleichungen nach auflösen und in ein Koordinatensystem einzeichnen. Anschließend brauchst du nur noch die Koordinaten des Schnittpunktes beider Geraden abzulesen.
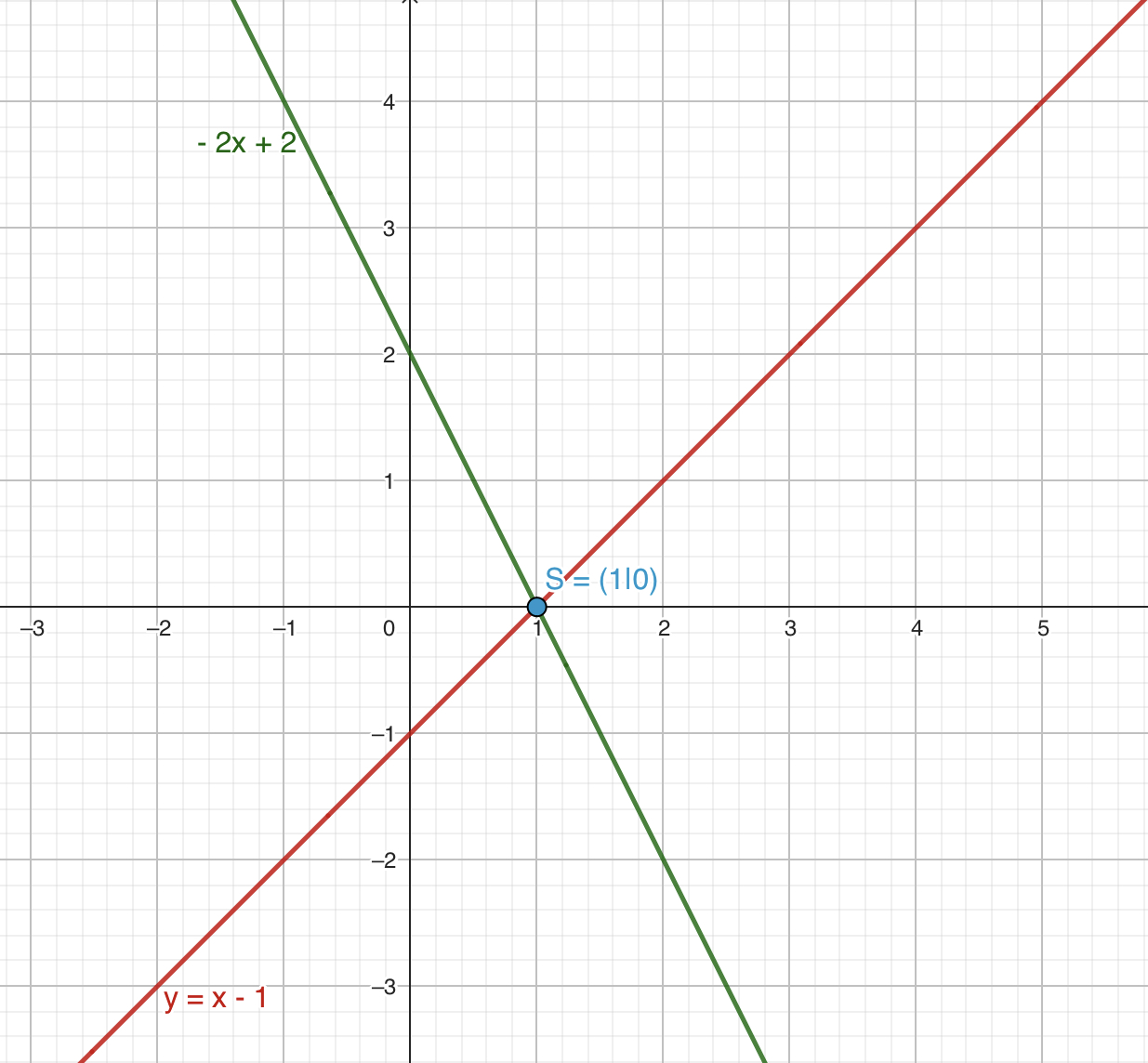
Der Schnittpunkt liegt bei und .
Rechnerisches Lösen
In diesem Fall bietet sich das Gleichsetzungsverfahren an, da du zum graphischen Lösen bereits beide Gleichungen nach aufgelöst hast.
Setze und gleich und löse nach auf.
Setze den erhaltenen Wert für in eine der Gleichungen ein, z.B in .
Antwort: Die Lösung ist und .
Hast du eine Frage oder Feedback?
Graphisches Lösen: Löse beide Gleichungen nach y auf, und zeichne die Graphen in ein Koordinatensystem.
Rechnerisches Lösen: Verwende das Gleichsetzungsverfahren.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Lineare Gleichungssysteme
Graphisches Lösen
Um das Gleichungssystem graphisch lösen zu können, kannst du die einzelnen Geichungen nach auflösen und in ein Koordinatensystem einzeichnen. Anschließend brauchst du nur noch die Koordinaten des Schnittpunktes beider Geraden abzulesen.
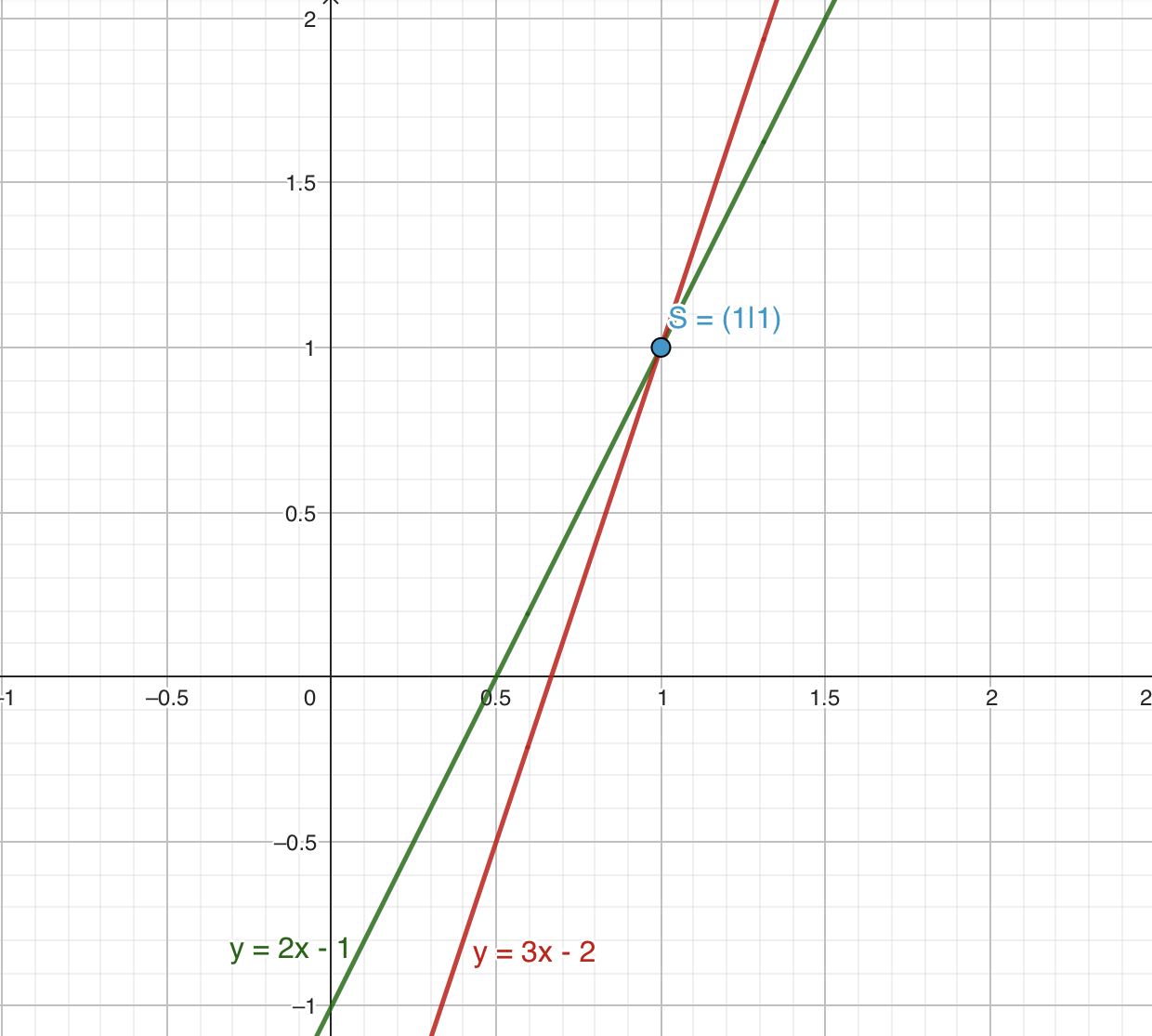
Der Schnittpunkt liegt bei und .
Rechnerisches Lösen
In diesem Fall bietet sich das Gleichsetzungsverfahren an, da du zum graphischen Lösen bereits beide Gleichungen nach aufgelöst hast.
Setze und gleich und löse nach auf.
Setze den erhaltenen Wert für in eine der Gleichungen ein, z.B in .
Antwort: Die Lösung ist und .
Hast du eine Frage oder Feedback?
Graphisches Lösen: Löse beide Gleichungen nach y auf, und zeichne die Graphen in ein Koordinatensystem.
Rechnerisches Lösen: Verwende das Gleichsetzungsverfahren.
- 5
Ein Hotel verfügt über 105 Betten, die sich in 40 Zwei-bzw.-Dreibettzimmern befinden. Wie viele Zwei-und-Dreibettzimmer kann das Hotel vermieten?
Löse mit einem Gleichungssystem!
Für diese Aufgabe benötigst Du folgendes Grundwissen: Lineares Gleichungssystem
Gleichungen aus dem Text aufstellen
Als erstes legt man die Variablen fest:
x: Anzahl der Zweibettzimmer
y: Anzahl der Dreibettzimmer
Was ist bekannt? Insgesamt gibt es 40 Zimmer. Die Anzahl der Zweibettzimmer und die Anzahl der Dreibettzimmer zusammen ergibt also 40:
Insgesamt gibt es 105 Betten. In einem Zweibettzimmer stehen 2 Betten, also gibt es in einem Zweibettzimmer Betten und in einem Dreibettzimmer Betten. Es entsteht also die Gleichung:
Es entsteht das Gleichungssystem:
Jetzt können wir das Gleichungssystem lösen. Hier bietet sich das Einsetzungsverfahren an, weil wir Gleichung leicht nach oder nach auflösen können. Wir lösen nach auf:
Jetzt können wir in einsetzen:
Erstelle aus dem Aufgabentext ein lineares Gleichungssystem.
Tipp: Wähle die Variable für die Anzahl der Zweibettzimmer und die Variable für die Anzahl der Dreibettzimmer.
- 6
Ein Bauer hält in seinem Stall Hühner und Kaninchen. Er zählt insgesamt 120 Beine. Es gibt dreimal mehr Hühner als Kaninchen. Wie viele Hühner und Kaninchen hat der Bauer?
Löse mit einem Gleichungssystem!
Für diese Aufgabe benötigst Du folgendes Grundwissen: Einsetzungsverfahren
Gleichungen aus dem Text aufstellen
Als erstes legt man die Variablen fest:
x: Anzahl der Hühner
: Anzahl der Kaninchen.
Was ist bekannt? Ein Huhn hat zwei Beine, ein Kaninchen hat vier Beine. Somit haben Hühner Beine und Kaninchen haben Beine. Daraus können wir Gleichung aufstellen:
"Es gibt dreimal mehr Hühner als Kaninchen": Weil die Anzahl der Kaninchen ist, müssen wir mit multiplizieren um die Anzahl der Hühner zu erhalten. Wir können nun Gleichung aufstellen:
Es entsteht das lineare Gleichungssystem:
Hier bietet sich das Einsetzungsverfahren an, da Gleichung schon nach der Variablen aufgelöst ist.
Lösung mit dem Einsetzungsverfahren
Setze Gleichung in Gleichung ein:
Setze in Gleichung ein:
Antwort: Der Bauer besitzt Hühner und Kaninchen.
Erstelle aus dem Aufgabentext ein lineares Gleichungssystem.
Tipp: Wähle die Variable für die Anzahl der Hühner und die Variable für die Anzahl der Kaninchen.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?
