Was geschieht hier wie von Zauberhand?
Du bekommst in diesem Artikel keine Schulung in Hexerei und Zauberei wie in Hogwarts. Das kann Physik nicht leisten.
Wir können allerdings nachvollziehbar erklären, warum sich bei bewegten Leitern in einem bestehenden Magnetfeld eine Ladungstrennung und dadurch induzierte Spannung einstellt.
Zur allgemeinen Einführung in das Thema raten wir Dir den Kurs zur Herleitung der Lorentzkraft zu wiederholen (--> LINK)
Lorentzkraft und Ladungsträgertrennung
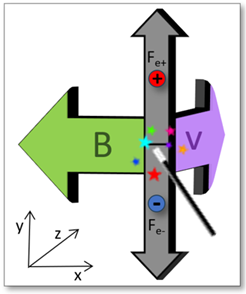
Innerhalb eines Magnetfeldes wirkt auf bewegte Ladungen (Elektronen und Protonen ) die Kraft .
Wir haben bereits im einführenden Kurs zur Lorentzkraft erfahren, wie wir die Richtungen der Lorentzkraft mit der Linke-Hand-Regel (für Elektronen) sowie der Rechte-Hand-Regel (für Protonen) ermitteln können.
Warum nun auch zu einer Ladungsträgertrennung führen muss, ist in nachfolgender Prinzipskizze (siehe Abb. 1) anschaulich darstellt:
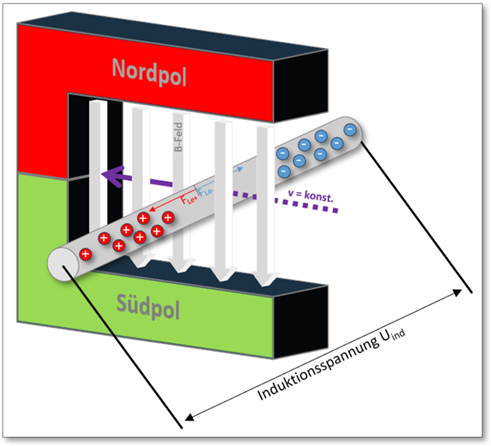
Abb. 1: Prinzipdarstellung der Ladungsträgertrennung als Vorgang der Induktion
Herleitung der Induktionsspannung am geraden Leiter
Nachfolgend möchten wir die logische Ableitung der Induktionsspannung darstellen:
Wenden wir uns deshalb zunächst der vorherigen Ladungsträgertrennung zu. Wie festgestellt ist hierbei verursachend die Kraft . Nur wie lange, bzw. bis zu welchem Maß kann diese Trennung (im Leiterstück nach links und rechts) fortgeführt werden, wann stellt sich ein Ende bzw. ein Gleichgewicht ein?
Dieses Gleichgewicht stellt sich ein durch ein entstehendes Elektrisches Feld . Warum?Werden auf der einen Seite positive Ladungen abgedrängt, auf der anderen negative Ladungen, ensteht dazwischen ein Elektrischen Feld . Einem Feld innewohnend ist auch immer eine elektrische Kraft , welche sich dahingegend auswirkt, dass sich die ausbildenden Gesamtladungen (weil positiv und negativ) nunmehr anziehen. Und zwar gegengerichtet zu welche sie abgedrängt hatte.
Erreicht nun der Betrag der elektrischen Anziehungskraft jenen der gegensätzlichen auseinandertreibenden Kraft , stellt sich ein Gleichgewicht ein. Die Verschiebung der Ladungen findet ein Ende, das aufgebaute elektrische Potential steht, die Induktionsspannung liegt an den Enden des Leiters an und kann entnommen werden. Dieser Zusammenhang siehe Abb. 2:
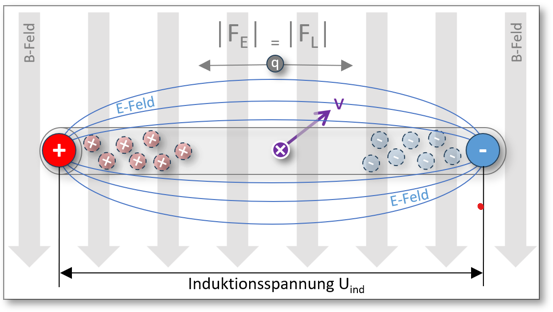
Abb. 2: Schematische Darstellung Kräftegleichgewicht und (abgeleitet aus Abb. 1)
Herleitung der Induktionsspannung an einer Leiterschleife
Bevor wir uns einem geeigneten Versuchsaufbau für Leiterschleifen widmen, müssen wir die uns bekannte Formel zur Berechnung der Induktionsspannung noch geringfügig anpassen, da sich eine Leiterschleife im Gegensatz zu einem Leiter flächig darstellt.
Es gilt hierbei:
Hinweise:
Die Einschränkung in Bezug auf werden wir in einem eigenen Artikel noch aufheben
Die Flußdichte sei vorab hier als Vektor definiert
Was sagt uns dieser formale Zusammenhang?
Gemäß LENZscher Regel ist die induzierte Spannung ihren verursachenden Größen gegengerichtet, also negativ, daher das "-".
Die induzierte Spannung ist umso höher, je höher die Magnetische Flußdichte B, je stärker also das Magnetische Feld ist.
Die induzierte Spannung ist umso höher, je höher die Flächenänderung je Zeit, je höher also die Flächenänderungs"geschwindigkeit" im Magnetischen Feld ist.
Für unsere weitere Betrachtung an dieser Stelle gilt zunächst folgendes:
Die Magnetische Flußdichte sei konstant und es gilt
Im nachfolgenden Versuch soll lediglich der Quotient untersucht werden!
Zunächst gilt, dass die logische Ableitung identisch ist, also eine Ladungstrennung und damit eine Induktionsspannung immer durch die Kraft verursacht ist. Wie wir gezeigt haben ist lediglich die formelle Ableitung unserer bisherigen Formel zu in Bezug auf eine Flächenänderung geringfügig angepasst worden.
Dieser Änderung soll nun nachfolgend dargestellter Versuchsaufbau in Abb. 3 Rechnung tragen:
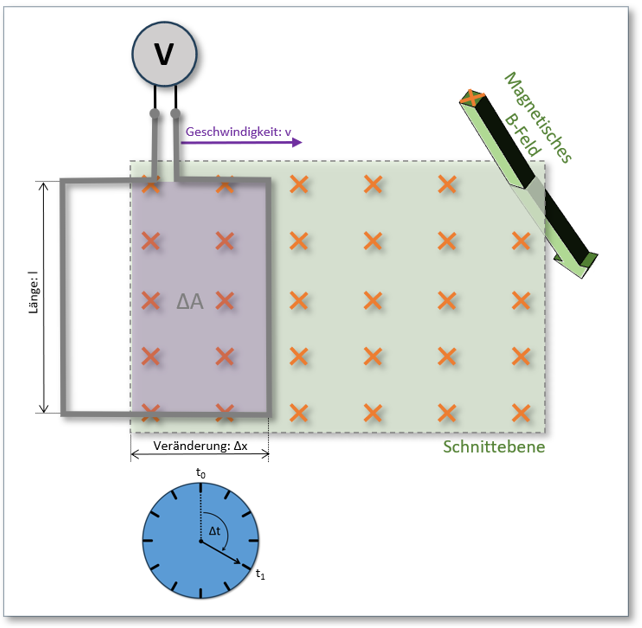
Abb. 3: Darstellung eines prinzipiellen Versuchsaufbaufs zur Messung von
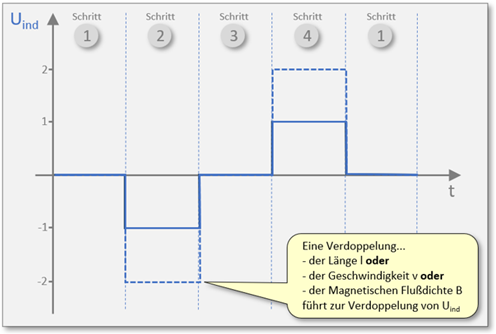
Schrittweise Abarbeitung des Versuches
Zum besseren Verständnis des Ablaufes sowie der Darstellung und des Zusammenhanges von Ursache und (Aus-)Wirkung, werden wir den Versuch aus Abb.: 3 in 4 Teilschritte unterteilen:
Teilschritt 1: Die Leiterschleife befindet sich ruhend oder bewegt sich vollständig außerhalb des konstanten Magnetfeldes
Teilschritt 2: Die Leiterschleife bewegt sich mit konstanter Geschwindigkeit in das Magnetfeld hinein
Teilschritt 3: Die Leiterschleife bewegt sich mit konstanter Geschwindigkeit im Magnetfeld
Teilschritt 4: Die Leiterschleife bewegt sich mit konstanter Geschwindigkeit aus dem Magnetfeld heraus
Ergebnis:
Leiterschleife ruhend: und hieraus folgt:
Leiterschleife bewegt: und hieraus folgt:
Anmerkung:
Es gilt für die ruhende wie die bewegte Leiterschleife, da Letztere nicht in das Magnetische Feld eintaucht und sich darin demnach auch nicht bewegt!
Dieser Teilschritt ist unabhängig davon identisch, ob sich die Leiterschleife nun links oder rechts vollständig außerhalb des Magnetfeldes befindet. Für letzteres könnte ein Teilschritt 5 definiert werden, welcher jedoch identisch zu 1 wäre.
Ergebnis:
und hieraus folgt:
Anmerkung:
Die Spannung wird erzeugt durch die von verursachte Ladungsverschiebung im rechten Teil der Leiterschleife. Diese Spannung kann am Voltmeter gemessen werden.
Ergebnis:
und hieraus folgt:
Anmerkungen:
beschreibt eine Flächenänderung pro Zeitintervall im Magnetfeld.. Ist diese (selbst bei ) ist keine Induktion einer Spannung möglich.
Im rechten und linken Teil der bewegten Leiterschleife wird durch gleichermaßen eine Ladungsverschiebung und damit gleichpolige Spannung verursacht. Am Spannungsmesser herrscht deshalb kein Potentialunterschied, wodurch keine Spannung gemessen werden kann.
Ergebnis:
und hieraus folgt:
Anmerkung:
Im Gegensatz zu Teilschritt wird nun im linken Teil der Leiterschleife eine Spannung induziert. Die am Voltmeter anliegende Spannung ist allerdings gegenpolig zu Teilschritt !
Der induzierte Spannungsverlauf nach Teilschritten
. . . es wird immer nur dann eine Spannung induziert, wenn eine durch das Magnetfeld durchströmte FlächenÄNDERUNG pro Zeiteinheit vorliegt:
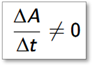
Übungsaufgaben
Laden
Quellen
- https://pixabay.com
- Bilder in Eigenkonstruktion
