Geometrie, Teil B, Aufgabengruppe 1

Gegeben sind die Punkte $A (8 ∣ 0 ∣ 6)$ , $B (7 ∣ 1 ∣ 6)$ und $S (0 ∣ 0 ∣ 10)$ , die in der

Ebene $E$ liegen.

Berechnen Sie die Länge der Strecke $[A B]$ und geben Sie die besondere
Lage dieser Strecke im Koordinatensystem an.
(zur Kontrolle: $\overline{AB}=\sqrt2$ )
Für diese Aufgabe benötigst Du folgendes Grundwissen: Länge eines Vektors
Berechne die Länge der Strecke $[A B]$
Berechne den Betrag des Vektors $\overrightarrow{AB}$ .
$\overrightarrow{AB}=\overrightarrow{OB}-\overrightarrow{OA}=\begin{pmatrix}7\\1\\6\end{pmatrix}-\begin{pmatrix}8\\0\\6\end{pmatrix}=\begin{pmatrix}-1\\1\\0\end{pmatrix}$
$\left|\overrightarrow{AB}\right|=\left|\begin{pmatrix}-1\\1\\0\end{pmatrix}\right|=\sqrt{(-1)^2+1^2+0^2}=\sqrt{2}$
Die besondere Lage dieser Strecke im Koordinatensystem
Die Strecke $[A B]$ ist parallel zur $x_{1} x_{2}$ -Ebene.
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Teil 1
Berechne den Betrag des Vektors $\overrightarrow{AB}$ .
Teil 2
Betrachte die $x_{3}$ -Koordinate des Vektors $\overrightarrow{AB}$ .
Bestimmen Sie eine Gleichung von $E$ in Koordinatenform.
(zur Kontrolle: $E : x_{1} + x_{2} + 2 x_{3} - 20 = 0$ )
Für diese Aufgabe benötigst Du folgendes Grundwissen: Ebene
Bestimme eine Gleichung von $E$ in Koordinatenform
Die Vektoren $\overrightarrow{AS}$ und $\overrightarrow{AB}$ sind die Richtungsvektoren der Ebene $E$ .
Berechne den Vektors $\overrightarrow{AS}$ .
$\overrightarrow{AS}=\overrightarrow{OS}-\overrightarrow{OA}=\begin{pmatrix}0\\0\\10\end{pmatrix}-\begin{pmatrix}8\\0\\6\end{pmatrix}=\begin{pmatrix}-8\\0\\4\end{pmatrix}=4\cdot\begin{pmatrix}-2\\0\\1\end{pmatrix}$
In Aufgabe a) wurde schon der Vektor $\overrightarrow{AB}=\begin{pmatrix}-1\\1\\0\end{pmatrix}$ berechnet.
Der Normalenvektor $\vec n$ der Ebene $E$ ist das Kreuzprodukt der beiden Richtungsvektoren.
$\vec n=\begin{pmatrix}-1\\1\\0\end{pmatrix}\times \begin{pmatrix}-2\\0\\1\end{pmatrix}=\begin{pmatrix}1\\1\\2\end{pmatrix}$
Dann folgt für die Gleichung der Ebene $E$ :
$E:\;\left(\overrightarrow{OX}-\overrightarrow{OS}\right)\circ\vec n=0\;\Rightarrow\;\left(\overrightarrow{OX}-\begin{pmatrix}0\\0\\10\end{pmatrix}\right)\circ\begin{pmatrix}1\\1\\2\end{pmatrix}=0$
Ausmultipliziert, erhält man die Koordinatenform von $E$ :
$\displaystyle x_1+x_2+2x_3-20=0$
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Die Vektoren $\overrightarrow{AS}$ und $\overrightarrow{AB}$ sind die Richtungsvektoren der Ebene $E$ .
Der Normalenvektor $\vec n$ der Ebene $E$ ist das Kreuzprodukt der beiden Richtungsvektoren.
Stelle die Gleichung der Ebene $E$ in Normalenform auf und wandle sie in die Koordinatenform um.

Betrachtet werden die Schar der Geraden $g_k:\overrightarrow{X}=\begin{pmatrix} 0 \\ 0 \\ 10\end{pmatrix}+\lambda\cdot\begin{pmatrix} 1+k \\ 1-k \\ -1 \end{pmatrix}$ mit $\lambda\in\mathbb{R}$ und $k\in\mathbb{R}$ sowie der Punkt $C (9 ∣ 1 ∣ 5)$ .

Begründen Sie, dass jede Gerade der Schar in $E$ liegt, und bestimmen Sie

denjenigen Wert $k$ , für den der Punkt $C$ auf $g_{k}$ liegt.

(zur Kontrolle: $k = 0,8$ ⁣)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Lagebeziehungen von Geraden und Ebenen

Begründe, dass jede Gerade der Schar in $E$ liegt

Setze die Gleichung der Geraden $g_{k}$ in $E$ ein:

$\displaystyle E : x_1+x_2+2x_3$	$=$	$\displaystyle 2 0$
	↓	Setze die Gleichung der Geraden $g_{k}$ in $E$ ein
$\displaystyle \lambda \cdot(1+k)+\lambda \cdot(1-k)+2\cdot (10-\lambda)$	$=$	$\displaystyle 20$
	↓	Löse die Klammern auf.
$\displaystyle \lambda +\lambda \cdot k+\lambda -\lambda \cdot k+20-2\lambda$	$=$	$\displaystyle 20$
	↓	Vereinfache
$\displaystyle 20$	$=$	$\displaystyle 20$

Du hast eine wahre Aussage erhalten, d.h. dass jede Gerade der Schar $g_{k}$ in $E$ liegt.

Bestimme denjenigen Wert $k$ , für den der Punkt $C$ auf $g_{k}$ liegt

$C\in g_k$ :

$\displaystyle g_k:\overrightarrow{X}$	$=$	$\displaystyle \begin{pmatrix} 0 \\ 0 \\ 10\end{pmatrix}+\lambda\cdot\begin{pmatrix} 1+k \\ 1-k \\ -1 \end{pmatrix}$
	↓	Setze $C (9 ∣ 1 ∣ 5)$ in $g_{k}$ für $\overrightarrow{X}$ ein.
$\displaystyle \begin{pmatrix}9\\1\\5\end{pmatrix}$	$=$	$\displaystyle \begin{pmatrix} 0 \\ 0 \\ 10\end{pmatrix}+\lambda\cdot\begin{pmatrix} 1+k \\ 1-k \\ -1 \end{pmatrix}$

Aus der 3. Gleichung folgt: $5=10-\lambda \;\Rightarrow\;\lambda=5$

Setze $\lambda=5$ in die 1. Gleichung ein:

$9=5\cdot(1+k)\;\Rightarrow\;9=5+5k\;\Rightarrow\;4=5k\;\Rightarrow\;k=\dfrac{4}{5}=0{,}8$

Überprüfe noch die 2. Gleichung:

$1=5\cdot(1-0{,}8)=5\cdot 0{,}2=1 \;\checkmark$

Für $k = 0,8$ liegt der Punkt $C$ auf $g_{k}$ .

Hast du eine Frage oder Feedback?

Kommentiere hier 👇

Begründen Sie, dass die Größe des Schnittwinkels von $g_{k}$ und der

$x_{1} x_{2}$ -Ebene weniger als $30^\circ$ beträgt, wenn $2k^2\gt 1$ gilt.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Schnittwinkel in der analytischen Geometrie

Begründe, dass die Größe des Schnittwinkels von $g_{k}$ und der $x_{1} x_{2}$ -Ebene weniger als $30^\circ$ beträgt, wenn $2k^2\gt 1$ gilt

Schnittwinkel Gerade Ebene:

$\sin\alpha=\dfrac{|\vec n\circ \vec u|}{|\vec n|\cdot|\vec u|}$

Der Richtungsvektor der Geraden ist dann der Vektor $\vec u=\begin{pmatrix} 1+k \\ 1-k \\ -1 \end{pmatrix}$ und der Normalenvektor der $x_{1} x_{2}$ -Ebene ist $\vec n=\begin{pmatrix}0\\0\\1\end{pmatrix}$ .

$\displaystyle \sin\alpha$	$=$	$\displaystyle \dfrac{\|\vec n\circ \vec u\|}{\|\vec n\|\cdot\|\vec u\|}$
	↓	Setze die Vektoren $\vec n$ und $\vec u$ ein.
	$=$	$\displaystyle \dfrac{\left\|\begin{pmatrix}0\\0\\1\end{pmatrix}\circ\begin{pmatrix} 1+k \\ 1-k \\ -1 \end{pmatrix}\right\|}{1\cdot\sqrt{(1+k)^2+(1-k)^2+(-1)^2}}$
	↓	Berechne das Skalarprodukt.
	$=$	$\displaystyle \dfrac{\left\|-1\right\|}{1\cdot\sqrt{(1+k)^2+(1-k)^2+(-1)^2}}$
	↓	Berechne den Betrag und die quadratischen Terme im Nenner.
	$=$	$\displaystyle \dfrac{1}{\sqrt{1+2k+k^2+1-2k+k^2+1}}$
	↓	Vereinfache
	$=$	$\displaystyle \dfrac{1}{\sqrt{2k^2+3}}$

Damit gilt: $\sin\alpha=\dfrac{1}{\sqrt{2k^2+3}}$ .

In der Aufgabenstellung ist gefordert, dass $2k^2\gt 1$ ist:

$\sin\alpha=\dfrac{1}{\sqrt{\underbrace{2k^2}_{>1}+3}}$ $\;\Rightarrow\;\sin\alpha=\dfrac{1}{\sqrt{\underbrace{2k^2+3}_{>4}}}\;\Rightarrow\;\sin\alpha=\dfrac{1}{\underbrace{\sqrt{2k^2+3}}_{>2}}<\dfrac{1}{2}$

Also ist $\sin\alpha<\dfrac{1}{2}$ .

Da $\sin30^\circ=\dfrac{1}{2}$ ist, folgt aus $\sin\alpha<\dfrac{1}{2}$ , dass $\alpha <30^\circ$ sein muss.

Der Schnittwinkel von $g_{k}$ und der $x_{1} x_{2}$ -Ebene beträgt also weniger als $30^\circ$ , wenn $2k^2\gt 1$ gilt.

Hast du eine Frage oder Feedback?

Kommentiere hier 👇

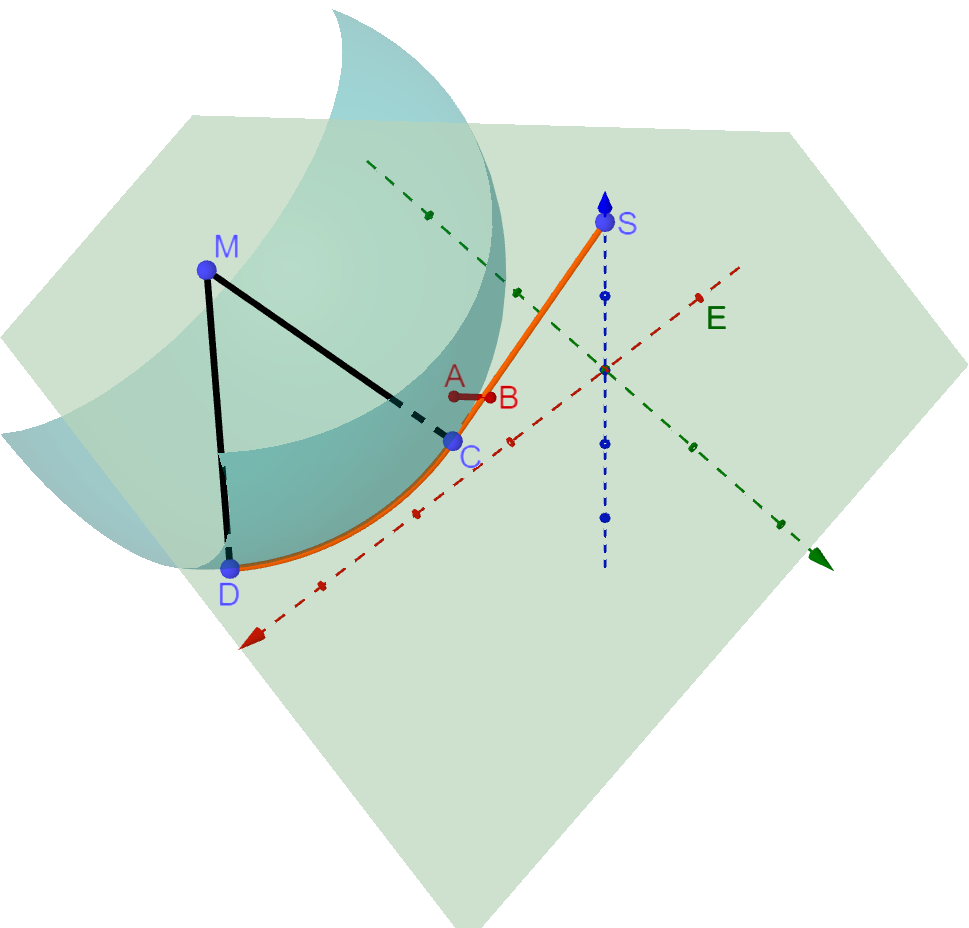
Eine Skifahrerin fährt einen Hang hinab. Dieser wird modellhaft durch ein Flächenstück beschrieben, das in der Ebene $E$ liegt. Die Startposition der Abfahrt entspricht dem Punkt $S$ . Auf dem Hang befindet sich ein Tor, dessen Begrenzungsstangen im Modell an den Punkten $A$ und $B$ stehen. Von ihrer Startposition fährt die Skifahrerin zunächst entlang einer geraden Fahrlinie bis zu einer Stelle unterhalb des Tors, die dem Punkt $C$ entspricht (vgl. Abbildung).
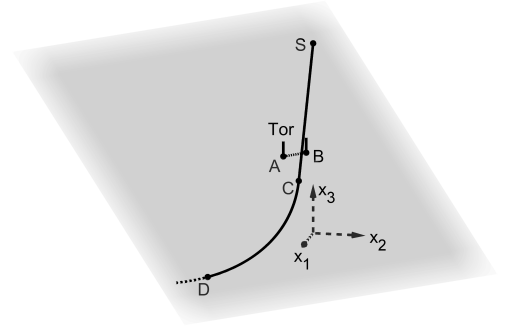
Die gerade Fahrlinie liegt dabei im Modell auf der Gerade
$g_{0{,}8}:\overrightarrow{X}=\begin{pmatrix} 0 \\ 0 \\ 10\end{pmatrix}+\lambda\cdot\begin{pmatrix} 1{,}8 \\ 0{,}2 \\ -1 \end{pmatrix}$
Die $x_{1} x_{2}$ -Ebene beschreibt die Horizontale; eine Längeneinheit im Koordinatensystem entspricht 5 Metern in der Realität.
Geben Sie mithilfe des Ergebnisses aus Aufgabe a) die Breite des Tors auf Meter genau an. Begründen Sie mithilfe der Aussage aus Aufgabe d), dass die gerade Fahrlinie der Skifahrerin um weniger als $30^\circ$ gegenüber der Horizontalen geneigt ist.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Länge eines Vektors
Gib mithilfe des Ergebnisses aus Aufgabe a) die Breite des Tors auf Meter genau an
In Aufgabe a) wurde der Betrag des Vektors $\left|\overrightarrow{AB}\right|=\sqrt{2}$ berechnet.
Da eine Längeneinheit im Koordinatensystem $5$ Metern in der Realität entspricht, ist die Torbreite $\sqrt{2}\cdot 5\;\mathrm{m}\approx 7\;\mathrm{m}$ .
Begründe mithilfe der Aussage aus Aufgabe d), dass die gerade Fahrlinie der Skifahrerin um weniger als $30^\circ$ gegenüber der Horizontalen geneigt ist
Aus Aufgabe d) folgt:
Der Schnittwinkel von $g_{k}$ und der $x_{1} x_{2}$ -Ebene beträgt also weniger als $30^\circ$ , wenn $2k^2\gt 1$ gilt.
Gegeben ist die Gerade $g_{0{,}8}$ , d.h. $k=0{,}8\;\Rightarrow\;2\cdot 0{,}8^2=1{,}28>1$ .
Die Bedingung für den Schnittwinkel von $g_{0{,}8}$ und der $x_{1} x_{2}$ -Ebene ist erfüllt.
Die gerade Fahrlinie der Skifahrerin ist um weniger als $30^\circ$ gegenüber der Horizontalen geneigt.
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Teil 1
In Aufgabe a) wurde der Betrag des Vektors $\left|\overrightarrow{AB}\right|$ berechnet. Beachte, dass eine Längeneinheit im Koordinatensystem $5$ Metern in der Realität entspricht.
Teil 2
Aus Aufgabe d) folgt: Der Schnittwinkel von $g_{k}$ und der $x_{1} x_{2}$ -Ebene beträgt weniger als $30^\circ$ , wenn $2k^2\gt 1$ gilt. Wie groß ist $k$ für die gegebene Gerade $g_{k}$ ?
Ist die Bedingung $2k^2\gt 1$ erfüllt?
Begründen Sie rechnerisch, dass die Skifahrerin das Tor tatsächlich durchquert.
Begründe rechnerisch, dass die Skifahrerin das Tor tatsächlich durchquert
Die gerade Fahrlinie liegt im Modell auf der Geraden $g_{0{,}8}:\overrightarrow{X}=\begin{pmatrix} 0 \\ 0 \\ 10\end{pmatrix}+\lambda\cdot\begin{pmatrix} 1{,}8 \\ 0{,}2 \\ -1 \end{pmatrix}$
$g_{AB}: \overrightarrow{X}=\overrightarrow{OA}+\mu\cdot \overrightarrow{AB}=\begin{pmatrix} 8 \\ 0 \\ 6\end{pmatrix}+\mu\cdot\begin{pmatrix}-1\\1\\0\end{pmatrix}$
Prüfe, ob die Gerade $g_{AB}$ durch die beiden Punkte $A$ und $B$ von $g_{0{,}8}$ geschnitten wird, setze $g_{0{,}8}=g_{AB}$ :
$\begin{pmatrix} 0 \\ 0 \\ 10\end{pmatrix}+\lambda\cdot\begin{pmatrix} 1{,}8 \\ 0{,}2 \\ -1 \end{pmatrix}=\begin{pmatrix} 8 \\ 0 \\ 6\end{pmatrix}+\mu\cdot\begin{pmatrix}-1\\1\\0\end{pmatrix}$
Aus Gleichung 3 folgt: $10-\lambda=6\;\Rightarrow\;\lambda=4$
Aus Gleichung 2 folgt: $0{,}2\cdot \lambda=\mu\;\Rightarrow\;\mu=0{,}2\cdot 4=0{,}8$
Die berechneten Werte werden in Gleichung 1 eingesetzt:
$1{,}8\cdot \lambda=8-\mu\;\Rightarrow\;1{,}8\cdot 4=8-0{,}8\;\Rightarrow\;7{,}2=7{,}2\;\checkmark$
Damit ist gezeigt, dass es einen Schnittpunkt zwischen den beiden Geraden gibt.
Der Schnittpunkt soll aber zwischen $A$ und $B$ liegen.
Für die Gerade $g_{AB}$ gilt:
Für $\mu=0$ ist $\overrightarrow{X}=\overrightarrow{OA}$ also der Punkt $A$ .
Für $\mu=1$ ist $\overrightarrow{X}=\overrightarrow{OB}$ also der Punkt B.
Für $0<\mu<1$ liegt der Geradenpunkt zwischen $A$ und $B$ .
Da hier $\mu=0{,}8$ berechnet wurde, liegt der Schnittpunkt zwischen $A$ und $B$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Prüfe, ob die Gerade $g_{AB}$ durch die beiden Punkte $A$ und $B$ von $g_{0{,}8}$ geschnitten wird.
Der Schnittpunkt liegt zwischen $A$ und $B$ , wenn für den Parameter $μ \mu$ der Geraden $g_{AB}$ gilt: $0<\mu<1$
An der Stelle, die im Modell dem Punkt $C$ entspricht, wird die Fahrlinie der Skifahrerin ohne Knick durch eine kreisbogenförmige Kurve fortgesetzt. Während der Fahrt entlang dieser Kurve erreicht die Skifahrerin eine Stelle, die dem Punkt $D (18 ∣ - 2 ∣ 2)$ entspricht.
Der Kreisbogen, der diese Kurve beschreibt, ist Teil eines Kreises mit Mittelpunkt $M (m_{1} ∣ m_{2} ∣ m_{3})$ . Die Koordinaten von $M$ können mit folgendem
Gleichungssystem ermittelt werden.
I $m_{1} + m_{2} + 2 m_{3} - 20 = 0$
II $\begin{pmatrix}m_1-9\\m_2-1 \\ m_3-5 \end{pmatrix}\circ\begin{pmatrix} 1{,}8 \\ 0{,}2 \\ -1 \end{pmatrix}=0$
III $\sqrt{(m_1-9)^2+(m_2-1)^2+(m_3-5)^2}=\sqrt{(m_1-18)^2+(m_2+2)^2+(m_3-2)^2}$
Erläutern Sie die geometrischen Überlegungen, die den Gleichungen I, II und III zugrunde liegen.
Erläutere die geometrischen Überlegungen, die den Gleichungen I, II und III zugrunde liegen
Gleichung I:
Der Mittelpunkt $M (m_{1} ∣ m_{2} ∣ m_{3})$ des Kreises liegt in der Ebene $E$ .
Seine Koordinaten erfüllen die Ebenengleichung.
Gleichung II:
Der Vektor $\begin{pmatrix}m_1-9\\m_2-1 \\ m_3-5 \end{pmatrix}$ ist der Vektor $\overrightarrow{CM}$ .
Dieser Vektor steht senkrecht auf dem Richtungsvektor $\begin{pmatrix} 1{,}8 \\ 0{,}2 \\ -1 \end{pmatrix}$ der Geraden $g_{0{,}8}$ . Das Skalarprodukt dieser beiden Vektor ist gleich null.
Die Gerade $g_{0{,}8}$ wird im Punkt $C$ vom Kreisbogen berührt.
Gleichung III:
Hier wurde zwei Beträge einander gleichgesetzt.
$\left|\overrightarrow{CM}\right|=\left|\overrightarrow{DM}\right|$
$\Rightarrow\;$ Die Punkte $C$ und $D$ haben den gleichen Abstand zum Punkt $M$ , liegen also auf dem Kreisbogen.
Die Abbildung ist in der Aufgabenstellung nicht verlangt worden.
Sie dient nur der Veranschaulichung.
Entlang der orangefarbigen Kurve fährt die Skifahrerin. Das Tor wird getroffen.
Anmerkung:
Der Kreis ist der Schnittpunkt einer Kugel mit Mittelpunkt $M$ mit der Ebene $E$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Gleichung I:
Vergleiche mit Aufgabe b)
Gleichung II:
Es ist ein Skalarprodukt gegeben, das den Wert null hat. Welche Schlussfolgerung folgt daraus? Aus welchen Vektoren wird das Skalarprodukt gebildet?
Gleichung III:
Hier sind zwei Beträge von Vektoren einander gleichgesetzt. Welche Vektoren sind das? Welche Schlussfolgerung kann man ziehen?

Berechne die Länge der Strecke [AB][AB][AB]

Die besondere Lage dieser Strecke im Koordinatensystem

Hast du eine Frage oder Feedback?

Bestimme eine Gleichung von EEE in Koordinatenform

Hast du eine Frage oder Feedback?

Begründe, dass jede Gerade der Schar in EEE liegt

Bestimme denjenigen Wert kkk, für den der Punkt CCC auf gkg_kgk​ liegt

Hast du eine Frage oder Feedback?

Begründe, dass die Größe des Schnittwinkels von gkg_kgk​ und der x1x2x_1x_2x1​x2​ -Ebene weniger als 30∘30^\circ30∘ beträgt, wenn 2k2>12k^2\gt 12k2>1 gilt

Hast du eine Frage oder Feedback?

Gib mithilfe des Ergebnisses aus Aufgabe a) die Breite des Tors auf Meter genau an

Begründe mithilfe der Aussage aus Aufgabe d), dass die gerade Fahrlinie der Skifahrerin um weniger als 30∘30^\circ30∘ gegenüber der Horizontalen geneigt ist

Hast du eine Frage oder Feedback?

Begründe rechnerisch, dass die Skifahrerin das Tor tatsächlich durchquert

Hast du eine Frage oder Feedback?

Erläutere die geometrischen Überlegungen, die den Gleichungen I, II und III zugrunde liegen

Hast du eine Frage oder Feedback?

Berechne die Länge der Strecke $[A B]$

Bestimme eine Gleichung von $E$ in Koordinatenform

Begründe, dass jede Gerade der Schar in $E$ liegt

Bestimme denjenigen Wert $k$ , für den der Punkt $C$ auf $g_{k}$ liegt

Begründe, dass die Größe des Schnittwinkels von $g_{k}$ und der $x_{1} x_{2}$ -Ebene weniger als $30^\circ$ beträgt, wenn $2k^2\gt 1$ gilt

Begründe mithilfe der Aussage aus Aufgabe d), dass die gerade Fahrlinie der Skifahrerin um weniger als $30^\circ$ gegenüber der Horizontalen geneigt ist