Zeige rechnerisch, dass für die Länge der Strecken $\overline{D{P}_n}$ in Abhängigkeit von $\phi$ gilt: $|\overline{D{P}_n}|(\phi )={\displaystyle \frac{11\cdot \sin \phi }{\sin ({\mathrm{35,54}}^{\circ }+\phi )}}\mathrm{cm}$

In beliebigen Dreiecken gilt der Sinussatz:

${\displaystyle \frac{a}{\sin \left(\alpha \right)}}={\displaystyle \frac{b}{\sin \left(\beta \right)}}={\displaystyle \frac{c}{\sin \left(\gamma \right)}}$

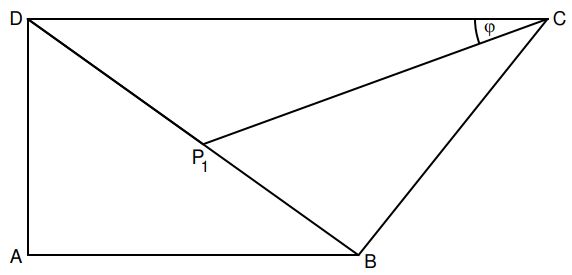
Angewandt auf das Dreieck $CD{P}_n$ folgt:

${\displaystyle \frac{|\overline{D{P}_n}|}{\sin \phi }}={\displaystyle \frac{|\overline{CD}|}{\sin \sphericalangle C{P}_{n}D}}$

Weiterhin gilt: $\sphericalangle C{P}_{n}D={180}^{\circ }-(\sphericalangle BDC+\phi )$

Für den Winkel $\sphericalangle BDC$ gilt: $\sphericalangle BDC={90}^{\circ }-\sphericalangle ADB$

Der Winkel $\sphericalangle ADB$ befindet sich im rechtwinkligen Dreieck $ABD$, sodass er berechnet werden kann.

$\tan \sphericalangle ADB={\displaystyle \frac{|\overline{AB}|}{|\overline{AD}|}}={\displaystyle \frac{7}{5}}=\mathrm{1,4}\Rightarrow \sphericalangle ADB={\tan }^{-1}(\mathrm{1,4})\approx {\mathrm{54,46}}^{\circ }$

Dann folgt für den Winkel $\sphericalangle BDC={90}^{\circ }-\sphericalangle ADB={90}^{\circ }-{\mathrm{54,46}}^{\circ }={\mathrm{35,54}}^{\circ }$

Nun kann auch der Winkel $\sphericalangle C{P}_{n}D={180}^{\circ }-(\sphericalangle BDC+\phi )$ angegeben werden:

$\sphericalangle C{P}_{n}D={180}^{\circ }-({\mathrm{35,54}}^{\circ }+\phi )$

Für den Ansatz mit dem Sinussatz erhält man nun:

${\displaystyle \frac{|\overline{D{P}_n}|}{\sin \phi }}={\displaystyle \frac{|\overline{CD}|}{\sin \sphericalangle C{P}_{n}D}}={\displaystyle \frac{|\overline{CD}|}{\sin ({180}^{\circ }-({\mathrm{35,54}}^{\circ }+\phi ))}}$

Wegen $\sin ({180}^{\circ }-\alpha )=\sin \alpha$ kann die rechte Seite der Gleichung noch umgeformt werden:

${\displaystyle \frac{|\overline{D{P}_n}|}{\sin \phi }}={\displaystyle \frac{|\overline{CD}|}{\sin ({180}^{\circ }-({\mathrm{35,54}}^{\circ }+\phi ))}}={\displaystyle \frac{|\overline{CD}|}{\sin ({\mathrm{35,54}}^{\circ }+\phi ))}}$

Aufgelöst nach $|\overline{D{P}_n}|$ erhält man:

$|\overline{D{P}_n}|={\displaystyle \frac{|\overline{CD}|\cdot \sin \phi }{\sin ({\mathrm{35,54}}^{\circ }+\phi ))}}$

Setzt man nun noch $|\overline{CD}|=11\mathrm{cm}$ ein, dann folgt:

$|\overline{D{P}_n}|={\displaystyle \frac{11\mathrm{cm}\cdot \sin \phi }{\sin ({\mathrm{35,54}}^{\circ }+\phi ))}}\Rightarrow |\overline{D{P}_n}|(\phi )={\displaystyle \frac{11\cdot \sin \phi }{\sin ({\mathrm{35,54}}^{\circ }+\phi )}}\mathrm{cm}$

Berechne die Länge der Strecke $\overline{D{P}_1}$

Der Winkel $\phi$ ist hier ${20}^{\circ }$.

Eingesetzt in $|\overline{D{P}_n}|(\phi )\Rightarrow |\overline{D{P}_1}|({20}^{\circ })={\displaystyle \frac{11\cdot \sin {20}^{\circ }}{\sin ({\mathrm{35,54}}^{\circ }+{20}^{\circ })}}\approx \mathrm{4,56}$

Die Länge der Strecke $\overline{D{P}_1}$ beträgt rund $\mathrm{4,56}\mathrm{cm}$.

Ergänze das Dreieck $CD{P}_2$ in der Zeichnung zur Aufgabenstellung

Das Dreieck $CD{P}_2$ ist gleichschenklig mit der Basis $\overline{CD}$.

Errichte die Mittelsenkrechte über der Strecke $\overline{CD}$.

Die Mittelsenkrechte schneidet die Strecke $\overline{BD}$ in Punkt $P_2$.

Siehe Zeichnung: