Aufgabe B 2
Die Vorlage einer Spielfigur ist ein Rotationskörper mit der Rotationsachse MS. Nebenstehende Skizze zeigt grau eingefärbt den zugehörigen Axialschnitt.
Es gilt: ;
.
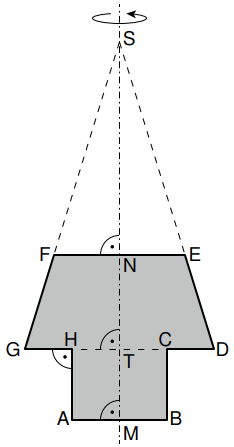
Berechnen Sie das Volumen des Rotationskörpers.
Runden Sie auf zwei Stellen nach dem Komma.
Zwischenergebnis: (4 P)
Die komplette Oberfläche der Spielfigur soll mit einer grauen Schutzfolie beklebt werden.
Welches Aufkleber-Set ist hierfür passend? Kreuzen Sie an. (1 P)