Aufgabe 2
Gegeben ist die in definierte Funktion mit . Der Graph von wird mit bezeichnet.
Geben Sie den Grenzwert von für an und begründen Sie Ihre Angabe anhand des Funktionsterms. (3 P)
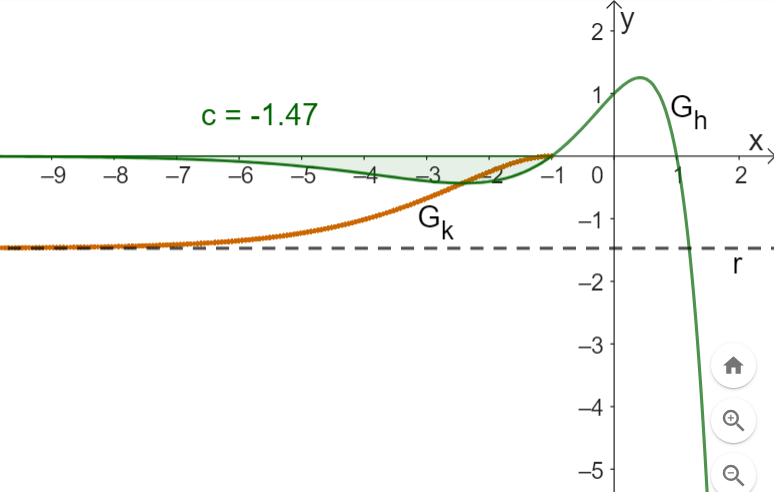
schließt mit der -Achse im ersten und zweiten Quadranten eine Fläche ein.
Die Gerade verläuft parallel zur -Achse durch den Hochpunkt von und teilt die Fläche in zwei Teilflächen.
Berechnen Sie den Anteil, den die größere der beiden Teilflächen an der Fläche hat.
(4 P)
Es gibt eine Zahl , sodass die Fläche, die , die -Achse und die Gerade mit der Gleichung im vierten Quadranten einschließen, den gleichen Inhalt hat wie die Fläche .
Bestimmen Sie . (3 P)
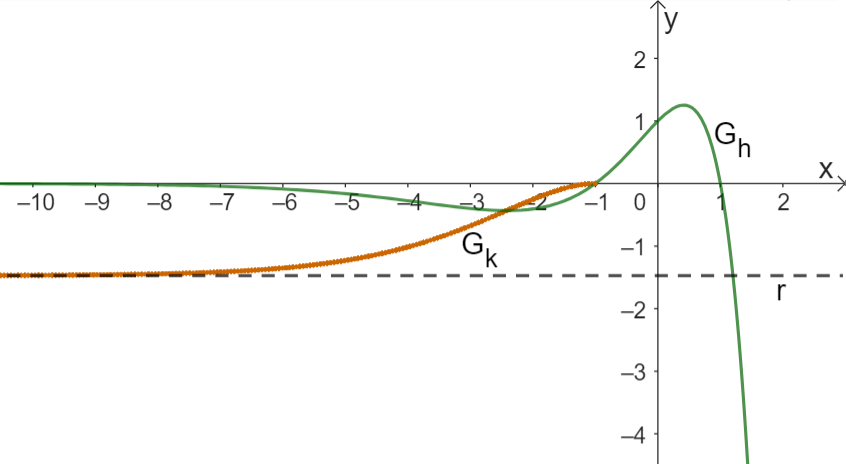
Abbildung
Gegeben ist die für definierte Funktion mit . Ihr Graph wird mit bezeichnet. Die Abbildung zeigt und . Für kommt der Geraden mit der Gleichung beliebig nahe.
(i) Begründen Sie mithilfe des Funktionsterms, dass die Nullstelle besitzt und dass im Bereich unterhalb der -Achse verläuft. (1 P+2 P)
(ii) Deuten Sie damit unter Verwendung der Abbildung den Wert in Bezug auf geometrisch. (2 P)
Die Funktion gehört zur Schar der in definierten Funktionen mit und . Der Graph von wird mit bezeichnet.
Ohne Nachweis darf im Folgenden verwendet werden: .
Begründen Sie anhand des Funktionsterms, dass für jedes die Funktionswerte von nur für positiv sind. (3 P)
Für jedes hat einen Hochpunkt, der im 1. Quadranten liegt. Es gibt einen Wert von , sodass die -Koordinate des Hochpunktes ist.
Bestimmen Sie diesen Wert von . (4 P)