Teil B: Analysis 1

🎓 Prüfungsbereich für Nordrhein-Westfalen

Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

Aufgabe 1

Ein mit Wasser befülltes Glas wird aus einem Kühlschrank genommen. Die anschließende Entwicklung der Wassertemperatur infolge der höheren Raumtemperatur lässt sich mithilfe der in $\mathbb{R}$ definierten Funktion $f: t \mapsto 25-20 \cdot \mathrm{e}^{-0{,}014 \cdot t}$ modellhaft beschreiben. Dabei ist $t$ die Zeit in Minuten, die seit der Entnahme aus dem Kühlschrank vergangen ist, und $f (t)$ die Wassertemperatur in ${ }^{\circ} \mathrm{C}$ . Die Raumtemperatur beträgt konstant $25^{\circ} \mathrm{C}$ .

(i) Geben Sie die Wassertemperatur zum Zeitpunkt der Entnahme aus dem Kühlschrank an. (1 P)
(ii) Bestimmen Sie den Zeitpunkt, zu dem die Wassertemperatur $12^{\circ} \mathrm{C}$ beträgt. (2 P)
Für diese Aufgabe benötigst Du folgendes Grundwissen: y-Achsenabschnitt
(i) Gib die Wassertemperatur zum Zeitpunkt der Entnahme aus dem Kühlschrank an
Es ist $f(t)=25-20 \cdot \mathrm{e}^{-0{,}014 \cdot t}$ .
Berechne $f (0)$ :
$f(0)=25-20 \cdot \mathrm{e}^{-0{,}014 \cdot 0}=25-20\cdot 1=5$
Zum Zeitpunkt der Entnahme aus dem Kühlschrank beträgt die Wassertemperatur $5^{\circ} \mathrm{C}$ .
(ii) Bestimme den Zeitpunkt, zu dem die Wassertemperatur $12^{\circ} \mathrm{C}$ beträgt
Löse die Gleichung $f (t) = 12$ mit dem GTR.
Betrachte die Graphen von $f$ und von $y = 12$ und bestimme ihren Schnittpunkt $t_1\approx 30{,}8$ .
Das Wasser hat rund $31$ Minuten nach Beobachtungsbeginn eine Temperatur von $12^{\circ} \mathrm{C}$ .
Die folgende Abbildung ist nicht in der Aufgabenstellung gefordert. Sie dient nur zur Veranschaulichung.
Schnittpunktbestimmung
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
(i)
Berechne $f (0)$ .
(ii)
Löse die Gleichung $f (t) = 12$ mit dem GTR.
Bestimmen Sie die mittlere Änderungsrate der Wassertemperatur innerhalb der ersten $30$ Minuten. (2 P)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Die mittlere Änderungsrate – Einführung der Ableitung
Bestimme die mittlere Änderungsrate der Wassertemperatur innerhalb der ersten $30$ Minuten
Für die mittlere Änderungsrate gilt:
$\dfrac{f(30)-f(0)}{30-0}=\dfrac{\left(25-20 \cdot \mathrm{e}^{-0{,}014 \cdot 30}\right)-5}{30}\approx0{,}23$
Die mittlere Änderungsrate der Wassertemperatur innerhalb der ersten $30$ Minuten beträgt rund $0{,}23 \;\frac{{ }^{\circ} \mathrm{C}}{\mathrm{min}}$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Für die mittlere Änderungsrate gilt allgemein: $\dfrac{f(t_2)-f(t_1)}{t_2-t_1}$
Setze $t_{2} = 30$ und $t_{1} = 0$ ein und vereinfache.
(i) Geben Sie $f^{\prime}(30)$ und die Bedeutung dieses Werts im Sachzusammenhang an. (2 P)
(ii) Für alle $t \in \mathbb{R}$ gilt: $f^{\prime}(t)>0$ und $f^{\prime \prime}(t)<0$ .
Erklären Sie, was diese Eigenschaften für die Entwicklung der Wassertemperatur im Glas bedeuten. (2 P)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Ableitung von Funktionen
(i) Geben Sie $f^{\prime}(30)$ und die Bedeutung dieses Werts im Sachzusammenhang an
Betrachte den Graphen von $f (x)$ :
Drücke eine beliebige Zahlentaste und gib für $x$ den Wert $30$ ein.
Angezeigt wird $\mathrm{\dfrac{dY}{dX}}\approx0{,}1839$ $\;\Rightarrow\;f'(30)\approx0{,}18$
$30$ Minuten nach der Entnahme aus dem Kühlschrank nimmt die Wassertemperatur mit einer momentanen Rate von etwa $0{,}18\;\frac{{}^\circ \text{C}}{\text{min}}$ zu.
ii) Für alle $t \in \mathbb{R}$ gilt: $f^{\prime}(t)>0$ und $f^{\prime \prime}(t)<0$ . Erkläre, was diese Eigenschaften für die Entwicklung der Wassertemperatur im Glas bedeuten
Wegen $f^{\prime}(t)>0$ nimmt die Wassertemperatur kontinuierlich zu.
Aus $f^{\prime \prime}(t)<0$ folgt, dass der Graph von $f$ nach rechts gekrümmt ist, d.h. die Wassertemperatur nimmt im Glas immer langsamer zu.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
(i)
Betrachte den Graphen von $f (x)$ . (Beim GTR $x$ statt $t$ .)
Gib für $x$ den Wert $30$ ein.
Angezeigt wird $\mathrm{\dfrac{dY}{dX}}$ , die erste Ableitung an der Stelle $x = 30$ , also $f^{'} (30)$ .
(ii)
Ist $f^{\prime}(t)>0$ nimmt die Wassertemperatur kontinuierlich zu.
Ist $f^{\prime \prime}(t)<0$ folgt, dass der Graph von $f$ nach rechts gekrümmt ist. Was folgt daraus für den Verlauf der Wassertemperatur?

Zeigen Sie, dass in diesem Modell gilt:

Es gibt eine Konstante $c$ , sodass zu jedem Zeitpunkt die Differenz zwischen der Raumtemperatur und der Wassertemperatur das $c$ -fache der momentanen Änderungsrate der Wassertemperatur ist. (3 P)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Gleichungen

Zeige, es gibt eine Konstante $c$ , sodass zu jedem Zeitpunkt die Differenz zwischen der Raumtemperatur und der Wassertemperatur das $c$ -fache der momentanen Änderungsrate der Wassertemperatur ist

Die Raumtemperatur beträgt $25^{\circ} \mathrm{C}$ und die Wassertemperatur ist $f (t)$ .

Die momentane Änderungsrate ist $f'(t)=-20\cdot \mathrm{e}^{-0{,}014 \cdot t}\cdot (-0{,}014)=0{,}28\cdot \mathrm{e}^{-0{,}014 \cdot t}$

Damit erhält man die folgende Gleichung:

$25-f(t)=c\cdot f'(t)$

$\Rightarrow\;25-\left(25-20 \cdot \mathrm{e}^{-0{,}014 \cdot t}\right)=c\cdot0{,}28\cdot \mathrm{e}^{-0{,}014 \cdot t}$

Löse die Gleichung nach t auf:

$\displaystyle 25-\left(25-20 \cdot \mathrm{e}^{-0{,}014 \cdot t}\right)$	$=$	$\displaystyle c\cdot0{,}28\cdot \mathrm{e}^{-0{,}014 \cdot t}$
	↓	Löse die Gleichung nach $t$ auf.
$\displaystyle 20 \cdot \mathrm{e}^{-0{,}014 \cdot t}$	$=$	$\displaystyle c\cdot0{,}28\cdot \mathrm{e}^{-0{,}014 \cdot t}$	$\displaystyle :\mathrm{e}^{-0{,}014 \cdot t}$
	↓	$\mathrm{e}^{-0{,}014 \cdot t}$ ist ungleich $0$ .
$\displaystyle 20$	$=$	$\displaystyle c\cdot 0{,}28$	$\displaystyle :0{,}28$
$\displaystyle \dfrac{20}{0{,}28}$	$=$	$\displaystyle c$
$\displaystyle 71{,}43$	$\approx ≈$	$\displaystyle c$

Die Gleichung hat somit unabhängig von $t$ die Lösung $c\approx 71{,}43$ .

Somit existiert die Konstante.

Hast du eine Frage oder Feedback?

Kommentiere hier 👉

Bei einem anderen Vorgang wird die Entwicklung der Temperatur von Wasser in einem zweiten Glas durch die in $\mathbb{R}$ definierte Funktion $g: t \mapsto 5+20 \cdot \mathrm{e}^{-0{,}014 t}$ modellhaft beschrieben. Dabei ist $t$ die seit Beobachtungsbeginn vergangene Zeit in Minuten und $g (t)$ die Wassertemperatur in ${ }^{\circ} \mathrm{C}$ . Bei den durch $f$ und $g$ beschriebenen Vorgängen sind die durch $t = 0$ festgelegten Zeitpunkte identisch.
Beschreiben Sie, durch welche Transformationen der Graph von $g$ aus dem Graphen von $f$ hervorgeht. (2 P)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Transformationen von Funktionen
Beschreibe, durch welche Transformationen der Graph von g aus dem Graphen von $f$ hervorgeht
Gegeben sind $f(t)=25-20 \cdot \mathrm{e}^{-0{,}014 \cdot t}$ und $g(t)=5+20 \cdot \mathrm{e}^{-0{,}014 t}$
$f\xrightarrow{\text{Spiegelung an t-Achse}}-f(t)=-25+20 \cdot \mathrm{e}^{-0{,}014 \cdot t}$ anschließend
$\xrightarrow{\text{Verschiebung um 30 in positive y-Richtung}}-25+20 \cdot \mathrm{e}^{-0{,}014 \cdot t}+30=5+20 \cdot \mathrm{e}^{-0{,}014 t}=g(t)$
Die Transformationen sind also:
Spiegelung an der t-Achse
Verschiebung um $30$ in positive y-Richtung
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Was bewirkt eine Spiegelung an der t-Achse?
Was ändert sich, wenn der Funktionsgraph in positive y-Richtung verschoben wird?
Beurteilen Sie jede der folgenden Aussagen:
$\mathrm{I}$ Die Temperatur des Wassers im zweiten Glas nimmt während des gesamten Beobachtungszeitraums ab. (2 P)
$\mathrm{II}$ Für beide Gläser stimmen zu jedem Zeitpunkt die Beträge der momentanen Änderungsraten der Wassertemperaturen überein. (2 P)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Ableitung von Funktionen
Beurteile jede der folgenden Aussagen:
$\mathrm{I}$ Die Temperatur des Wassers im zweiten Glas nimmt während des gesamten Beobachtungszeitraums ab.
Gegeben ist $g(t)=5+20 \cdot \mathrm{e}^{-0{,}014 t}$ . Dann ist $g'(t)=-0{,}28 \cdot e^{-0{,}014 t}$ .
Die Aussage $\mathrm{I}$ ist richtig.
Begründung:
Wegen $g^{\prime}(t)=-0{,}28 \cdot e^{-0{,}014 t}<0$ ist für alle $t \in \mathbb{R}$ die Funktion $g$ streng monoton fallend, d.h. die Temperatur nimmt stetig ab.
$\mathrm{II}$ Für beide Gläser stimmen zu jedem Zeitpunkt die Beträge der momentanen Änderungsraten der Wassertemperaturen überein
Die Aussage $\mathrm{II}$ ist richtig.
Begründung:
Es ist $g'(t)=-0{,}28 \cdot e^{-0{,}014 t}=-f'(t)$
Für jedes $t \in \mathbb{R}$ stimmen die Beträge der momentanen Änderungsraten überein.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Teil I
Berechne $g^{'} (t)$ . Was bedeutet es, wenn die Ableitung negativ ist?
Teil II
Vergleiche die Beträge der beiden Ableitungen $g^{'} (t)$ und $f^{'} (t)$ .

Aufgabe 2

Gegeben ist die in $\mathbb{R}$ definierte Funktion $h$ mit $h(x)=\left(1-x^{2}\right) \cdot \mathrm{e}^{x}$ . Der Graph von $h$ wird mit $G_{h}$ bezeichnet.

Geben Sie den Grenzwert von $h$ für $x \rightarrow-\infty$ an und begründen Sie Ihre Angabe anhand des Funktionsterms. (3 P)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Grenzwert bestimmen
Gib den Grenzwert von $h$ für $x \rightarrow-\infty$ an und begründe Deine Angabe anhand des Funktionsterms
Gegeben ist $h(x)=\left(1-x^{2}\right) \cdot \mathrm{e}^{x}$ .
Dann gilt:
$\displaystyle\lim_{x\rightarrow -\infty}\underbrace{\left(1-x^{2}\right)}_{\rightarrow -\infty}\cdot \underbrace{\mathrm{e}^{x}}_{\rightarrow 0}=0$
$e^{x}$ geht stärker gegen $0$ als $(1 - x^{2})$ gegen minus unendlich geht.
Der Grenzwert von $h$ für $x \rightarrow-\infty$ ist gleich null.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Betrachte die einzelnen Faktoren.
$G_{h}$ schließt mit der $x$ -Achse im ersten und zweiten Quadranten eine Fläche $A$ ein.
Die Gerade $m$ verläuft parallel zur $y$ -Achse durch den Hochpunkt $H(-1+\sqrt{2} \mid h(-1+\sqrt{2}))$ von $G_{h}$ und teilt die Fläche $A$ in zwei Teilflächen.
Berechnen Sie den Anteil, den die größere der beiden Teilflächen an der Fläche $A$ hat.
(4 P)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Flächenberechnung mit Integralen
Berechne den Anteil, den die größere der beiden Teilflächen an der Fläche $A$ hat
Für die Nullstellen von $h$ gilt: $h(x)=0 \Leftrightarrow x=-1$ oder $x = 1$ .
Der Inhalt der Fläche $A$ entspricht dem Wert des Integrals $\displaystyle\int_{-1}^{1} h(x)\; \mathrm{d} x$ .
Die beiden Flächen $A_{1}$ und $A_{2}$
Zur Veranschaulichung wurde die obige Zeichnung angefertigt.
Man erkennt, dass die größere Fläche die Fläche $A_{2}$ ist.
Gesucht ist also das Verhältnis $\dfrac{A_2}{A}$ :
$\dfrac{A_2}{A}=\frac{\displaystyle\int_{-1}^{-1+\sqrt{2}} h(x)\; \mathrm{d} x}{\displaystyle\int_{-1}^{1} h(x) \;\mathrm{d} x} \approx 0{,}647$
Der Anteil, den die größere der beiden Teilflächen an der Fläche $A$ hat, beträgt rund $64{,}7\ \%$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Berechne die Nullstellen von $h$ $\;\Rightarrow\;x_1$ und $x_{2}$
Der Inhalt der Fläche $A$ entspricht dem Wert des Integrals $\displaystyle\int_{x_1}^{x_2} h(x)\; \mathrm{d} x$ .
Welche der beiden Teilflächen hat den größeren Flächeninhalt $\;\Rightarrow\;A_{\text{größer}}$
Berechne dann das Verhältnis $\dfrac{A_{\text{größer}}}{A}$ .
Es gibt eine Zahl $b > 1$ , sodass die Fläche, die $G_{h}$ , die $x$ -Achse und die Gerade mit der Gleichung $x = b$ im vierten Quadranten einschließen, den gleichen Inhalt hat wie die Fläche $A$ .
Bestimmen Sie $b$ . (3 P)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Flächenberechnung mit Integralen
Bestimme $b$
Zur Veranschaulichung wurde eine Zeichnung angefertigt:
Zwei gleich große Flächen
Die orangefarbige Fläche soll den gleichen Flächeninhalt haben wie die grüne Fläche.
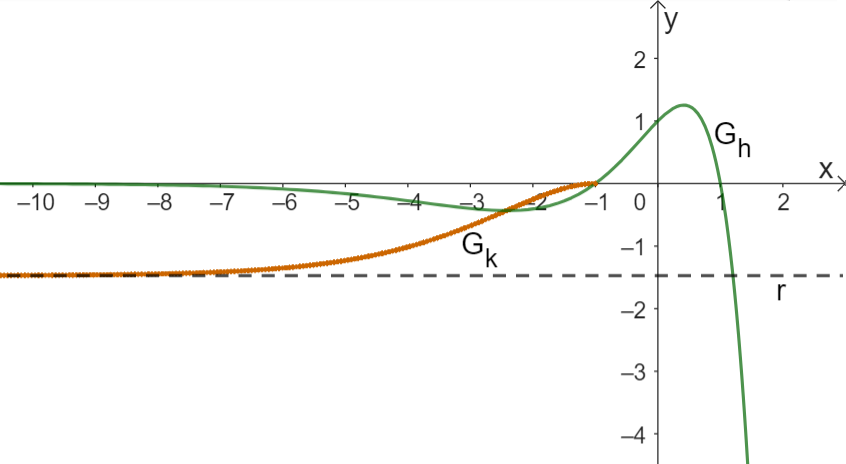
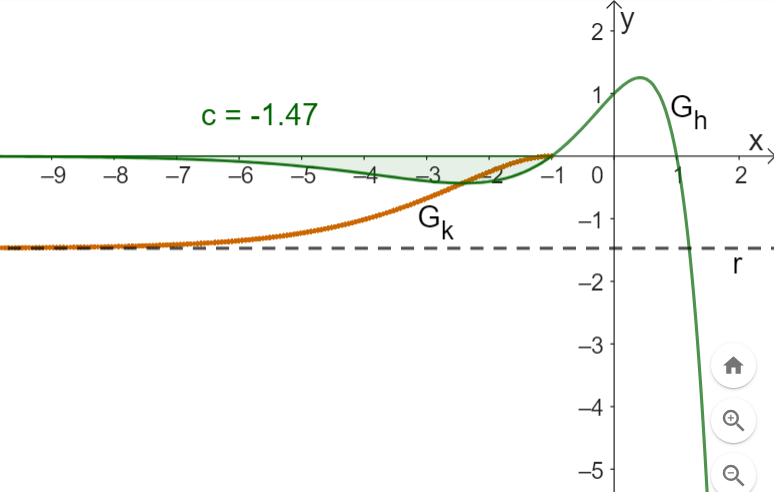
Da die orangefarbige Fläche unterhalb der x-Achse liegt, gilt:
$A_{\text{grün}}+A_{\text{orange}}=0\;\Rightarrow\; \displaystyle\int_{-1}^{b} h(x) \;\mathrm{d} x=0$
Diese Gleichung kann mit $\text{nsolve}$ gelöst werden und man erhält für $b > 1$ die Lösung $b \approx 1{,}55692...$ .
Für $b\approx1{,}56$ hat die Fläche, die $G_{h}$ , die $x$ -Achse und die Gerade mit der Gleichung $x = b$ im vierten Quadranten einschließen, den gleichen Inhalt wie die Fläche $A$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Die Fläche $A$ liegt oberhalb der x-Achse.
Die Fläche $\displaystyle\int_{1}^{b} h(x) \;\mathrm{d} x$ liegt unterhalb der x-Achse.
Beide Flächen sind für $b > 1$ gleich groß, wenn $\displaystyle\int_{-1}^{b} h(x) \;\mathrm{d} x=0$ ist.
Abbildung
Gegeben ist die für $x \leq-1$ definierte Funktion $k$ mit $k(x)=\displaystyle\int_{x}^{-1} h(t) \mathrm{d} t$ . Ihr Graph wird mit $G_{k}$ bezeichnet. Die Abbildung zeigt $G_{h}$ und $G_{k}$ . Für $x \rightarrow-\infty$ kommt $G_{k}$ der Geraden $r$ mit der Gleichung $y=-\frac{4}{\mathrm{e}}$ beliebig nahe.
(i) Begründen Sie mithilfe des Funktionsterms, dass $k$ die Nullstelle $- 1$ besitzt und dass $G_{k}$ im Bereich $x < - 1$ unterhalb der $x$ -Achse verläuft. (1 P+2 P)
(ii) Deuten Sie damit unter Verwendung der Abbildung den Wert $-\frac{4}{\mathrm{e}}$ in Bezug auf $G_{h}$ geometrisch. (2 P)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Flächenberechnung mit Integralen
(i) Begründe mithilfe des Funktionsterms, dass $k$ die Nullstelle $- 1$ besitzt
Es gilt:
$k(-1)=\displaystyle\int_{-1}^{-1} h(x)\; \mathrm{d} x=0$ wegen der übereinstimmenden Grenzen des Integrals.
(i) Begründe mithilfe des Funktionsterms, dass $G_{k}$ im Bereich $x < - 1$ unterhalb der $x$ -Achse verläuft
Die Funktion $h (x) < 0$ für $x < - 1$ . (siehe Abbildung bei d)
Deshalb ist für $x < - 1$ auch $k (x) < 0$ .
(ii) Deute damit unter Verwendung der Abbildung den Wert $-\frac{4}{\mathrm{e}}$ in Bezug auf $G_{h}$ geometrisch
Zur Veranschaulichung wurde eine Zeichnung angefertigt:
Fläche unterhalb der x-Achse
Für $c < - 1$ gibt $k (c)$ den orientierten Inhalt der Fläche an, die $G_{h}$ und die $x$ -Achse zwischen den Geraden mit den Gleichungen $x = c$ und $x = - 1$ einschließen.
Die Annäherung von $G_{k}$ an die Gerade $r$ mit der Gleichung $y=-\frac{4}{\mathrm{e}}$ bedeutet daher für $G_{h}$ geometrisch, dass der Inhalt der oben beschriebenen Fläche für kleiner werdende Werte von $c$ dem Wert $\frac{4}{\mathrm{e}}$ beliebig nahekommt.
In der Zeichnung ist der Wert des Integrals $k(-12)=\displaystyle\int_{-12}^{-1} h(t)\; \mathrm{d} t\approx-1{,}47$ angegeben (grüne Fläche) $\;\Rightarrow\;$ $-\dfrac{4}{e}\approx-1{,}4715...$
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
(i)
Teil 1
Wenn die Grenzen des Integrals übereinstimmen, ist der Wert des Integrals gleich null.
Teil 2
Die Funktion $h (x) < 0$ für $x < - 1$ . Welche Folgen hat das für $k (x)$ ?
(ii)
Für $c < - 1$ gibt $k (c)$ den orientierten Inhalt der Fläche an, die $G_{h}$ und die $x$ -Achse zwischen den Geraden mit den Gleichungen $x = c$ und $x = - 1$ einschließen.
Welchem Wert nähert sich diese Fläche für kleiner werdendes $c$ an?
Die Funktion $h$ gehört zur Schar der in $\mathbb{R}$ definierten Funktionen $h_{a}$ mit $h_{a}(x)=\frac{1}{a} \cdot\left(a-x^{2}\right) \cdot \mathrm{e}^{x}$ und $a > 0$ . Der Graph von $h_{a}$ wird mit $G_{h_{a}}$ bezeichnet.
Ohne Nachweis darf im Folgenden verwendet werden: $h_{a}{ }^{\prime}(x)=-\frac{1}{a} \cdot\left(x^{2}+2 x-a\right) \cdot e^{x}$ .
Begründen Sie anhand des Funktionsterms, dass für jedes $a > 0$ die Funktionswerte von $h_{a}$ nur für $-\sqrt{a}<x<\sqrt{a}$ positiv sind. (3 P)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Funktionswert
Begründe anhand des Funktionsterms, dass für jedes $a > 0$ die Funktionswerte von $h_{a}$ nur für $-\sqrt{a}<x<\sqrt{a}$ positiv sind
Gegeben ist: $h_{a}(x)=\frac{1}{a} \cdot\left(a-x^{2}\right) \cdot \mathrm{e}^{x}$
Gefordert wird, dass für jedes $a > 0$ die Funktionswerte von $h_{a}$ positiv sein sollen.
Dann folgt daraus:
$h_{a}(x)=\underbrace{\frac{1}{a}}_{>0\;\text{weil}\;a>0} \cdot\underbrace{\left(a-x^{2}\right)}_{>0} \cdot \underbrace{\mathrm{e}^{x}}_{>0\;\text{für alle x}\;}$
Demnach muss $a - x^{2} > 0$ sein $\;\Rightarrow\;a>x^2\;\Rightarrow\;\sqrt{a}>|x|$ .
Für $x\geq 0$ ist $x<\sqrt{a}$ .
Für $x < 0$ ist $-x<\sqrt{a}\;\Rightarrow\;x>-\sqrt{a}$
Zusammengefasst gilt dann: $-\sqrt{a}<x<\sqrt{a}$ ,
Für jedes $a > 0$ sind die Funktionswerte von $h_{a}$ nur für $-\sqrt{a}<x<\sqrt{a}$ positiv.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Betrachte die drei Terme, aus denen sich $h (x)$ zusammensetzt. Alle drei Terme müssen größer null sein, damit $h (x) > 0$ ist.
Untersuche dann den 2. Term.

Für jedes $a > 0$ hat $G_{h_{a}}$ einen Hochpunkt, der im 1. Quadranten liegt. Es gibt einen Wert von $a$ , sodass die $x$ -Koordinate des Hochpunktes $2$ ist.

Bestimmen Sie diesen Wert von $a$ . (4 P)

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

$\displaystyle -1+\sqrt{1+a}$	$=$	$\displaystyle 2$	$\displaystyle +1$
	↓	Löse nach $a$ auf.
$\displaystyle \sqrt{1+a}$	$=$	$\displaystyle 3$	$\displaystyle ()^2$
$\displaystyle 1+a$	$=$	$\displaystyle 9$	$\displaystyle -1$
$\displaystyle a$	$=$	$\displaystyle 8$

Teil B: Analysis 1

Aufgabe 1

(i) Gib die Wassertemperatur zum Zeitpunkt der Entnahme aus dem Kühlschrank an

(ii) Bestimme den Zeitpunkt, zu dem die Wassertemperatur 12∘C12^{\circ} \mathrm{C}12∘C beträgt

Hast du eine Frage oder Feedback?

Bestimme die mittlere Änderungsrate der Wassertemperatur innerhalb der ersten 303030 Minuten

Hast du eine Frage oder Feedback?

(i) Geben Sie f′(30)f^{\prime}(30)f′(30) und die Bedeutung dieses Werts im Sachzusammenhang an

ii) Für alle t∈Rt \in \mathbb{R}t∈R gilt: f′(t)>0f^{\prime}(t)>0f′(t)>0 und f′′(t)<0f^{\prime \prime}(t)<0f′′(t)<0. Erkläre, was diese Eigenschaften für die Entwicklung der Wassertemperatur im Glas bedeuten

Hast du eine Frage oder Feedback?

Zeige, es gibt eine Konstante ccc, sodass zu jedem Zeitpunkt die Differenz zwischen der Raumtemperatur und der Wassertemperatur das ccc-fache der momentanen Änderungsrate der Wassertemperatur ist

Hast du eine Frage oder Feedback?

Beschreibe, durch welche Transformationen der Graph von g aus dem Graphen von fff hervorgeht

Hast du eine Frage oder Feedback?

Beurteile jede der folgenden Aussagen:

I\mathrm{I}I Die Temperatur des Wassers im zweiten Glas nimmt während des gesamten Beobachtungszeitraums ab.

II\mathrm{II}II Für beide Gläser stimmen zu jedem Zeitpunkt die Beträge der momentanen Änderungsraten der Wassertemperaturen überein

Hast du eine Frage oder Feedback?

Aufgabe 2

Gib den Grenzwert von hhh für x→−∞x \rightarrow-\inftyx→−∞ an und begründe Deine Angabe anhand des Funktionsterms

Hast du eine Frage oder Feedback?

Berechne den Anteil, den die größere der beiden Teilflächen an der Fläche AAA hat

Hast du eine Frage oder Feedback?

Bestimme bbb

Hast du eine Frage oder Feedback?

(i) Begründe mithilfe des Funktionsterms, dass kkk die Nullstelle −1-1−1 besitzt

(i) Begründe mithilfe des Funktionsterms, dass GkG_{k}Gk​ im Bereich x<−1x<-1x<−1 unterhalb der xxx-Achse verläuft

(ii) Deute damit unter Verwendung der Abbildung den Wert −4e-\frac{4}{\mathrm{e}}−e4​ in Bezug auf GhG_{h}Gh​ geometrisch

Hast du eine Frage oder Feedback?

Begründe anhand des Funktionsterms, dass für jedes a>0a>0a>0 die Funktionswerte von hah_{a}ha​ nur für −a<x<a-\sqrt{a}<x<\sqrt{a}−a​<x<a​ positiv sind

Hast du eine Frage oder Feedback?

Bestimme diesen Wert von aaa

Hast du eine Frage oder Feedback?

(ii) Bestimme den Zeitpunkt, zu dem die Wassertemperatur $12^{\circ} \mathrm{C}$ beträgt

Bestimme die mittlere Änderungsrate der Wassertemperatur innerhalb der ersten $30$ Minuten

(i) Geben Sie $f^{\prime}(30)$ und die Bedeutung dieses Werts im Sachzusammenhang an

ii) Für alle $t \in \mathbb{R}$ gilt: $f^{\prime}(t)>0$ und $f^{\prime \prime}(t)<0$ . Erkläre, was diese Eigenschaften für die Entwicklung der Wassertemperatur im Glas bedeuten

Zeige, es gibt eine Konstante $c$ , sodass zu jedem Zeitpunkt die Differenz zwischen der Raumtemperatur und der Wassertemperatur das $c$ -fache der momentanen Änderungsrate der Wassertemperatur ist

Beschreibe, durch welche Transformationen der Graph von g aus dem Graphen von $f$ hervorgeht

$\mathrm{I}$ Die Temperatur des Wassers im zweiten Glas nimmt während des gesamten Beobachtungszeitraums ab.

$\mathrm{II}$ Für beide Gläser stimmen zu jedem Zeitpunkt die Beträge der momentanen Änderungsraten der Wassertemperaturen überein

Gib den Grenzwert von $h$ für $x \rightarrow-\infty$ an und begründe Deine Angabe anhand des Funktionsterms

Berechne den Anteil, den die größere der beiden Teilflächen an der Fläche $A$ hat

Bestimme $b$

(i) Begründe mithilfe des Funktionsterms, dass $k$ die Nullstelle $- 1$ besitzt

(i) Begründe mithilfe des Funktionsterms, dass $G_{k}$ im Bereich $x < - 1$ unterhalb der $x$ -Achse verläuft

(ii) Deute damit unter Verwendung der Abbildung den Wert $-\frac{4}{\mathrm{e}}$ in Bezug auf $G_{h}$ geometrisch

Begründe anhand des Funktionsterms, dass für jedes $a > 0$ die Funktionswerte von $h_{a}$ nur für $-\sqrt{a}<x<\sqrt{a}$ positiv sind

Bestimme diesen Wert von $a$