Für diese Aufgabe benötigst Du folgendes Grundwissen: Kreisumfang und Kreisfläche
Berechnen der Kreisfläche.
Die Formel zur Berechnung der Kreisfläche lautet:
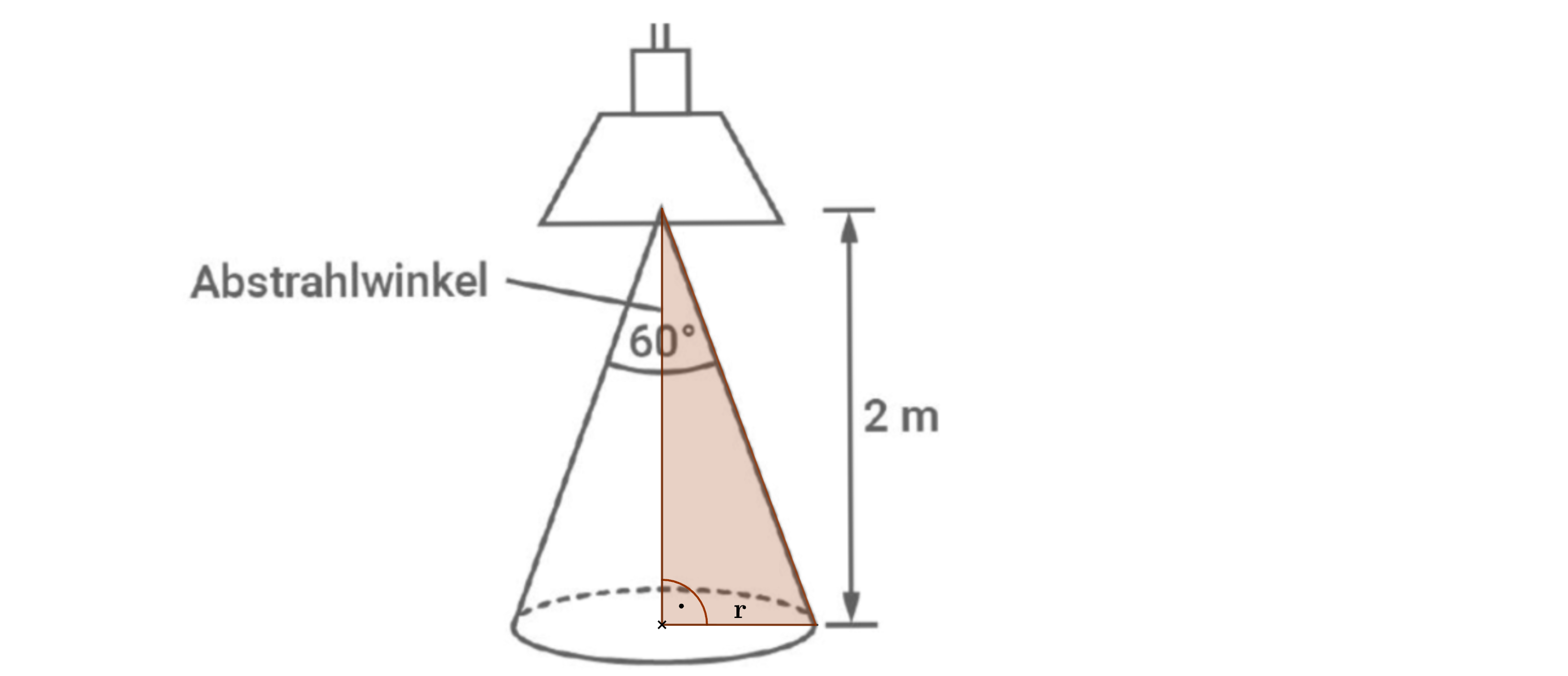
Berechnen des Radius mithilfe des Tangens.
Im rechtwinkligen Dreieck gilt:
Angewandt auf das farbig markierte Dreieck:
Der Flächeninhalt des Kreises beträgt:.
Berechnen des Mindestabstands der Lampe vom Tisch.
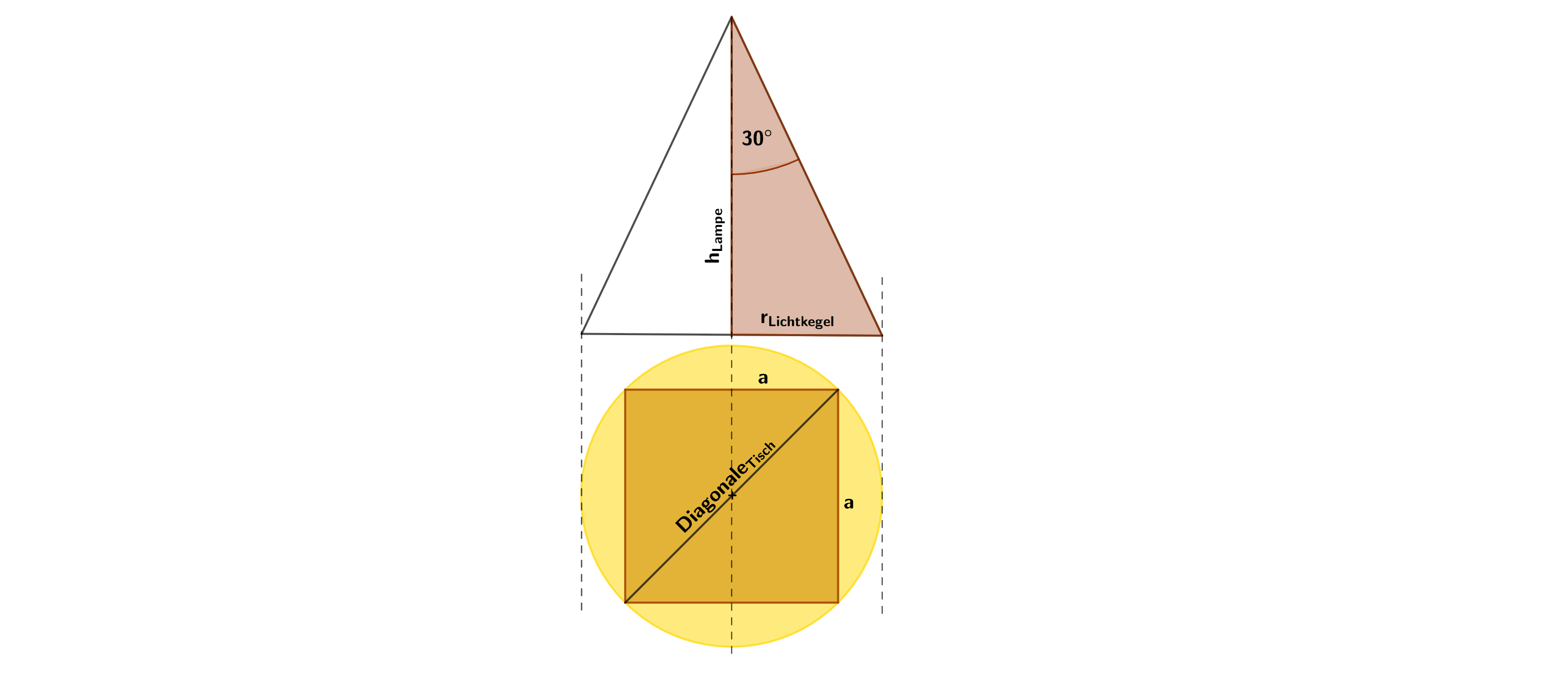
Damit der Tisch vollständig ausgeleuchtet wird, muss der Durchmesser des Lichtkegels mindestens so gross wie die Diagonale des Tisches sein.
Berechnen der Diagonale des Tisches.
Der Radius des Lichtkegels ist dann:
Berechnen der Höhe der Lampe mithilfe des Tangens.
Der Mindestabstand der Lampe vom Tisch beträgt ca. .
Bestimmen, ab welcher Leuchtdauer in Stunden sich der Einsatz von Leuchtmittel 1 im Vergleich zu Leuchtmittel 2 lohnt.
Aufstellen der Funktionsgleichungen für Leuchtmittel 1 und Leuchtmittel 2.
Leuchtmittel 1:Leuchtmittel 2:
Gleichsetzen der Funktionsgleichungen und berechnen von :
Berechnen von x. |
| ↓ |
| | | |
| ↓ | subtrahieren |
| | | |
| ↓ | subtrahieren |
| | | |
| ↓ | multiplizieren |
| | | |
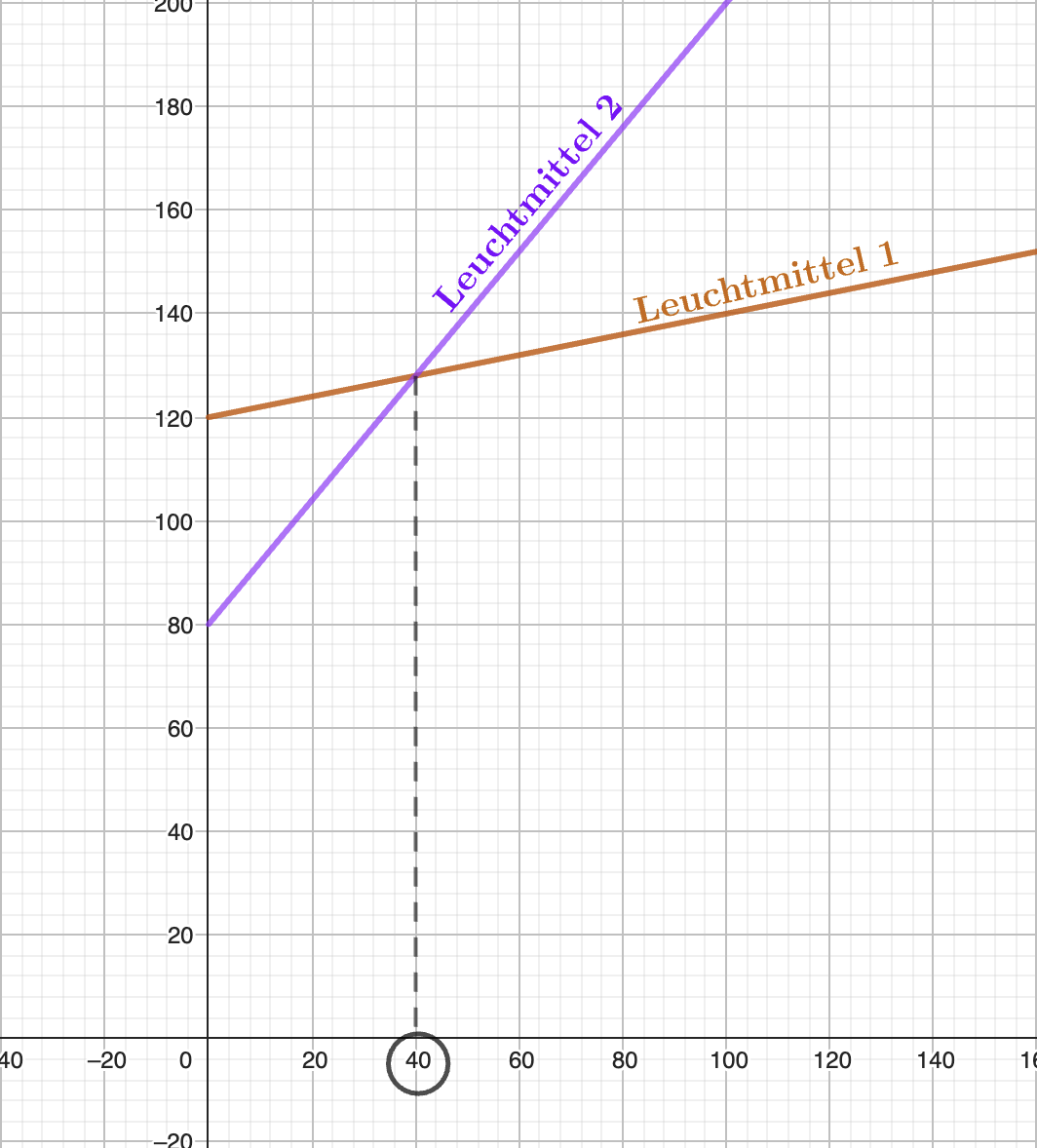
Die Grafik braucht nicht erstellt zu werden.
Der Einsatz von Leuchtmittel 1 im Vergleich zu Leuchtmittel 2, lohnt sich ab einer Leuchtdauer von mehr als Stunden.
Berechnen des Winkels .
Das Dreieck ist ein rechtwinkliges Dreieck, da der Punkt auf dem Thaleskreis liegt.
Das Dreieck ist ein gleichschenkliges Dreieck.
da diese Strecken Radien des Halbkreises sind.
In einem gleichschenkligenDreieck sind die Basiswinkel gleich groß.
Der Winkel ist dann:
Berechnen des Winkels :
Da die Winkel undNebenwinkel sind, gilt:
Der Winkel beträgt:.
Berechnen der Länge der Strecke .
Da das Dreieck rechtwinklig ist, kann die Strecke mithilfe des Sinus berechnet werden.
Im rechtwinkligem Dreieck gilt:
Angewandt auf das Dreieck :
Die Länge der Strecke ist beträgt:.
Berechnen des Flächeninhalts der grauen Fläche.
Berechnen der Fläche des Halbkreises:
Berechnen der Fläche des Dreiecks :
Berechnen des Flächeninhalts der grauen Fläche:
Der Flächeninhalt der grauen Fläche beträgt:.
Ermitteln der Schnittpunkte der Parabel mit der Geraden .
Gleichsetzen der Funktionsgleichungen der Parabel und der Geraden .
Berechnen von x. |
| ↓ |
| | | |
| ↓ | subtrahieren |
| | | |
| ↓ | (x) ausklammern |
| | | |
| ↓ | (x) Null setzen |
| | | |
| | | |
| ↓ | addieren |
| | | |
| ↓ | dividieren |
| | | |
Einsetzen der beiden -Werte z. B. in die Funktionsgleichung der Geraden .
Die Schnittpunkte der Parabel und der Geraden sind dann:
und