Zeichne die Graphen der Funktionen mit folgender Funktionsgleichung:
Für diese Aufgabe benötigst Du folgendes Grundwissen: lineare Funktionen
Einen Punkt ermitteln
entspricht der allgemeinen Geradengleichung und ist damit der Schnittpunkt mit der y-Achse .
Steigung ermitteln
Bestimme die Steigung der Funktion
entspricht der allgemeinen Geradengleichung und ist damit die Steigung der Geraden.
Gerade zeichnen
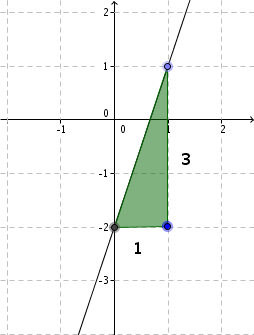
Gehe von dem zuvor ermittelten Punkt eine Einheit nach rechts und 3 nach oben, da m gleich 3 ist. Hier befindet sich ein zweiter Punkt der Funktion.
Verbinde anschließend die beiden Punkte zu einer Geraden.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: lineare Funktionen
Gleichung umstellen
Die Gleichung wird umgestellt, damit sie das Format der allgemeinen Geradengleichung hat.
Einen Punkt ermitteln
entspricht der allgemeinen Geradengleichung und ist damit der Schnittpunkt mit der y-Achse .
Steigung ermitteln
Bestimme nun die Steigung.
entspricht der allgemeinen Geradengleichung und ist damit die Steigung der Geraden.
Gerade zeichnen
Von dem zuvor ermittelten Punkt eine Einheit nach rechts und entsprechend m, nach unten gehen, da m negativ ist. Hier befindet sich ein zweiter Punkt der Funktion .
Anschließend die beiden Punkte zu einer Geraden verbinden.
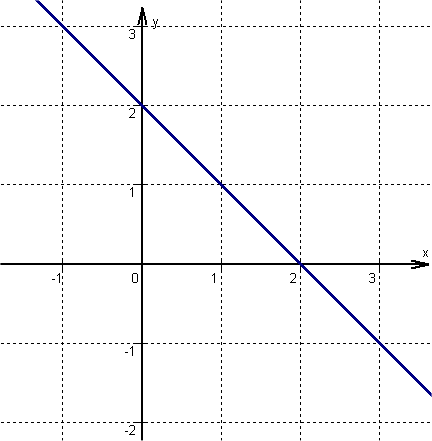
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: lineare Funktionen
Ein Punkt ermitteln
entspricht der allgemeinen Geradengleichung und ist damit der Schnittpunkt mit der y-Achse .
Steigung ermitteln
Bestimme nun die Steigung.
entspricht der allgemeinen Geradengleichung und ist damit die Steigung der Geraden.
Gerade zeichnen
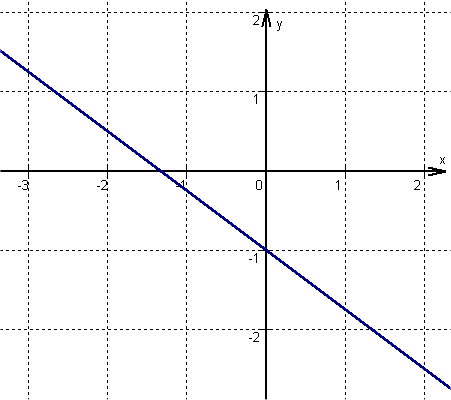
Von dem zuvor ermittelten Punkt eine Einheit nach rechts und entsprechend , nach unten gehen, da m negativ ist. Hier befindet sich ein zweiter Punkt der Funktion.
Anschließend die beiden Punkte zu einer Geraden verbinden.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: lineare Funktionen
Einen Punkt ermitteln
entspricht der allgemeinen Geradengleichung und ist damit der Schnittpunkt mit der y-Achse .
Steigung ermitteln
Bestimme nun die Steigung.
entspricht der allgemeinen Geradengleichung und ist damit die Steigung der Geraden.
Gerade zeichnen
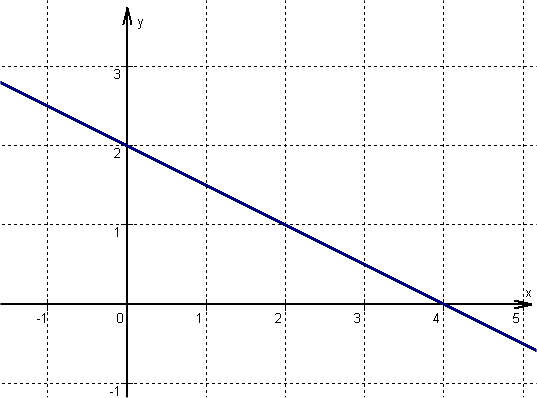
Von dem zuvor ermittelten Punkt eine Einheit nach rechts und entsprechend , nach unten gehen, da m negativ ist. Hier befindet sich ein zweiter Punkt der Funktion .
Anschließend die beiden Punkte zu einer Geraden verbinden.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: lineare Funktionen
Einen Punkt ermitteln
entspricht der allgemeinen Geradengleichung und ist damit der Schnittpunkt mit der y-Achse .
Steigung ermitteln
Bestimme nun die Steigung.
entspricht m der allgemeinen Geradengleichung und ist damit die Steigung der Geraden.
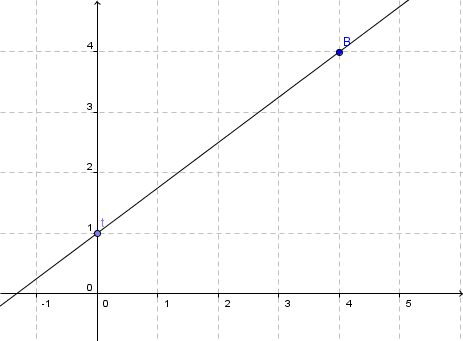
Gerade zeichnen
Von dem zuvor ermittelten Punkt eine Einheit nach rechts und entsprechend m, nach oben gehen, da m positiv ist. Hier befindet sich ein zweiter Punkt der Funktion .
Anschließend die beiden Punkte zu einer Geraden verbinden.
Hast du eine Frage oder Feedback?
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?
