Aufgaben zum Zeichnen von Graphen linearer Funktionen
Hier findest du Aufgaben zum Zeichnen von Geraden. Lerne, Graphen von linearen Funktionen zu skizzieren!
- 1
Zeichne anhand der gegebenen Wertetabelle den zugehörigen Graphen.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Gerade im Koordinatensystem
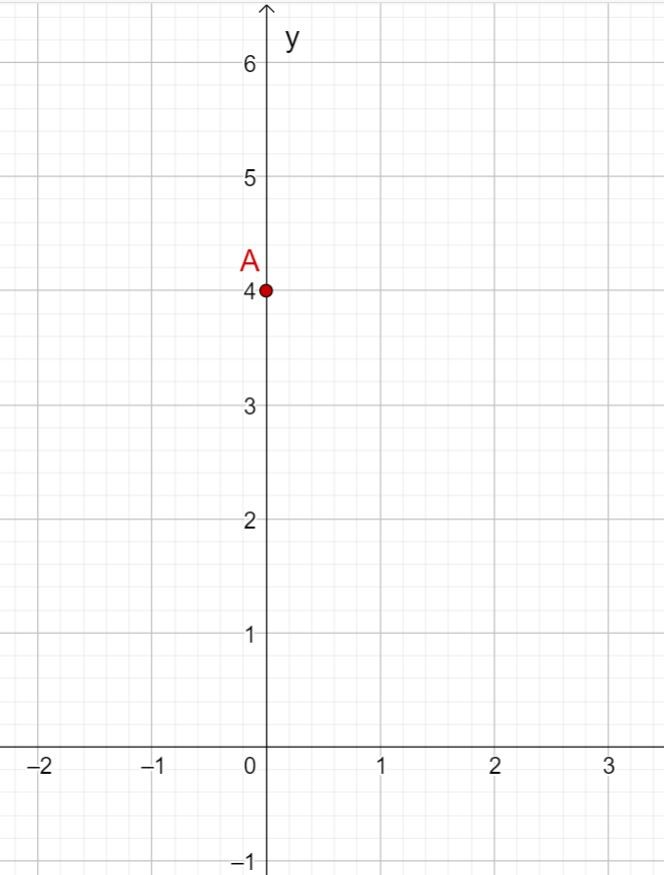
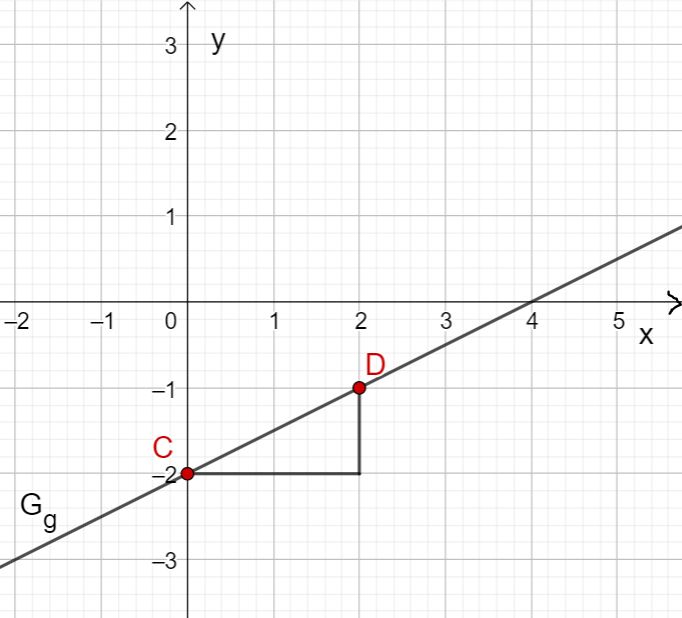
Zeichne die fünf gegebenen Punkte in ein Koordinatensystem und ziehe eine Gerade durch die Punkte.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Gerade im Koordinatensystem
Zeichne die vier gegebenen Punkte in ein Koordinatensystem und ziehe eine Gerade durch die Punkte.
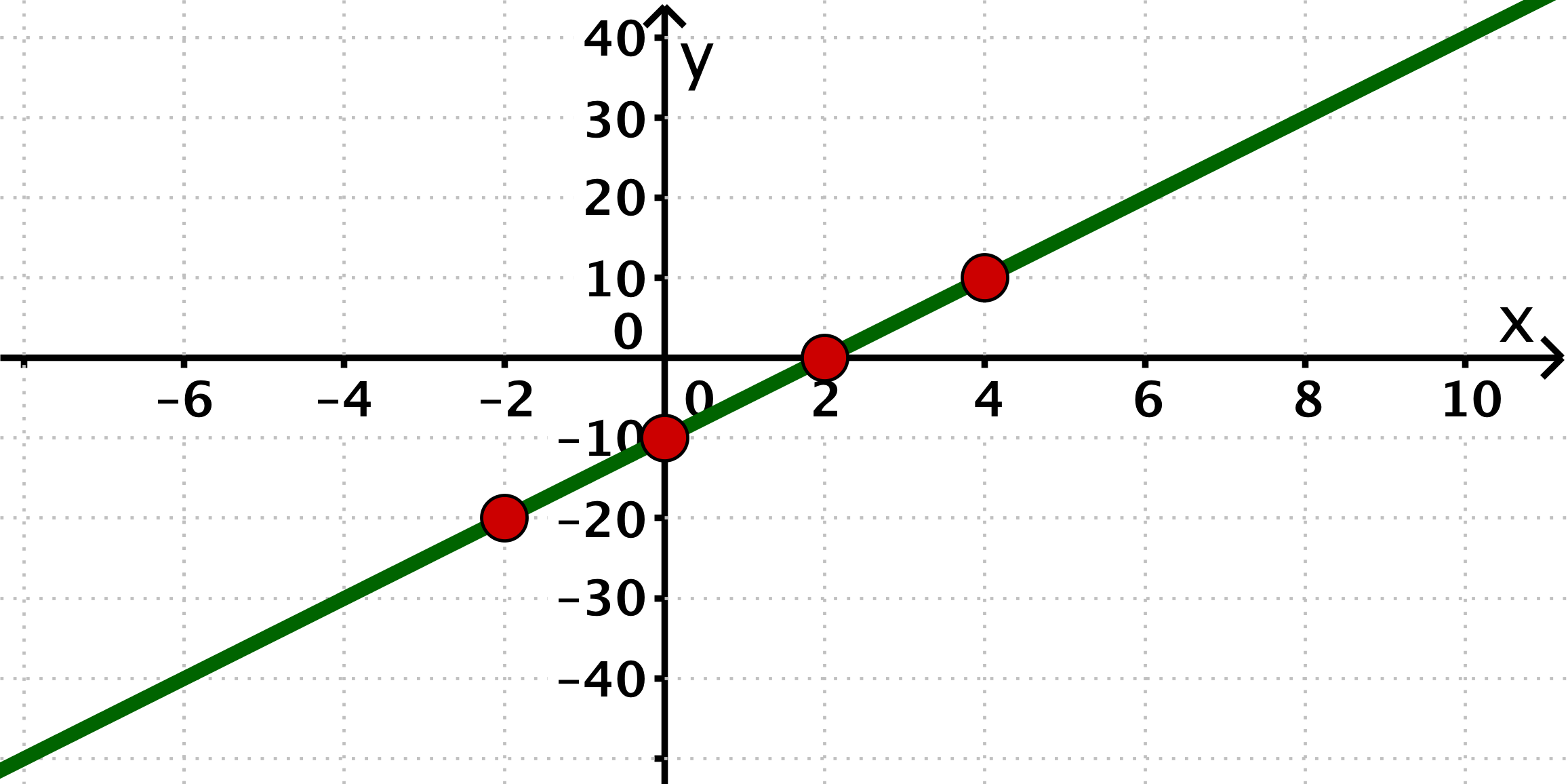
Hast du eine Frage oder Feedback?
- 2
Zeichne den Graphen der linearen Funktionen in ein Koordinatensystem ein!
Für diese Aufgabe benötigst Du folgendes Grundwissen: Funktionsterm linearer Funktionen
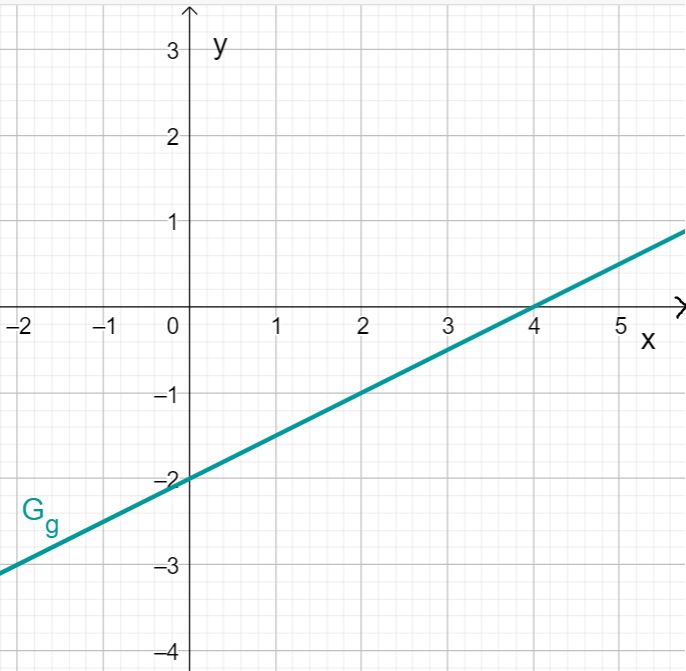
Zeichnen der linearen Funktion
Lese zunächst -Achsenabschnitt und die Steigung aus dem Funktionsterm der linearen Funktion ab.
In diesem Fall:
Du erhältst für den -Achsenabschnitt und für die Steigung .
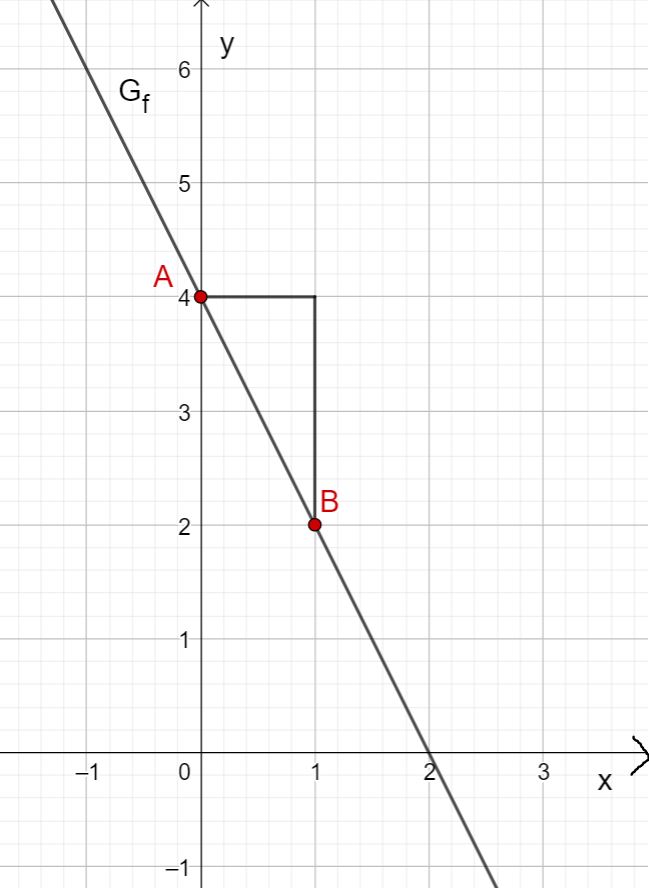
Zeichne zuerst den Schnittpunkt mit der -Achse ein, der sich durch den -Achsenabschnitt ergibt. Dieser lautet also .
Zeichne anschließend mithilfe der Steigung ein Steigungsdreieck. Gehe dafür eine Längeneinheit nach rechts und zwei Längeneinheiten nach unten. Dadurch erhältst du den Punkt . Ziehe nun die Gerade durch die Punkte und .
Du erhältst den Graphen von .
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Funktionsterm der linearen Funktion
Zeichnen der linearen Funktion
Lese zunächst -Achsenabschnitt und die Steigung aus dem Funktionsterm der linearen Funktion ab.
In diesem Fall:
Du erhältst für den -Achsenabschnitt und für die Steigung .
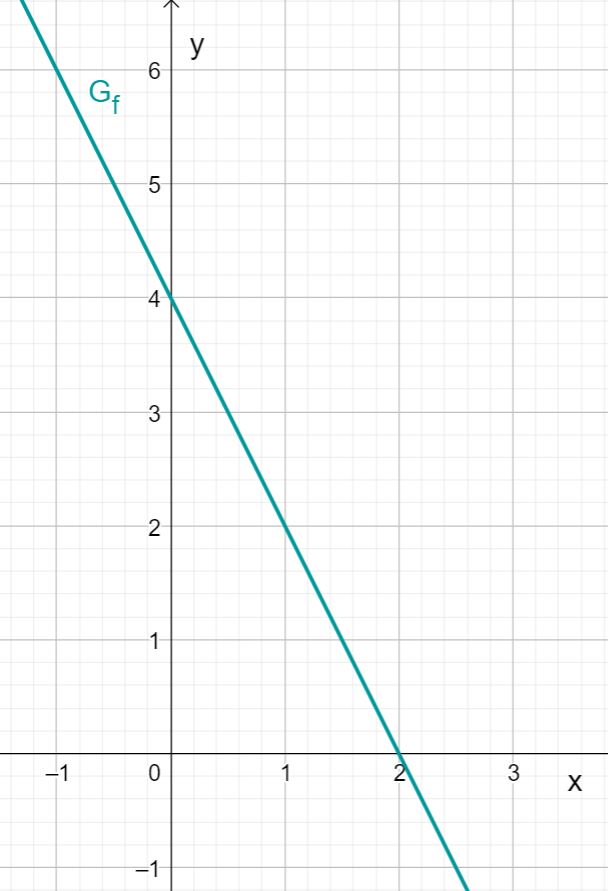
Zeichne zuerst den Schnittpunkt mit der -Achse ein, der sich durch den -Achsenabschnitt ergibt. Dieser lautet also .
Zeichne anschließend mithilfe der Steigung ein Steigungsdreieck. Gehe dafür zwei Längeneinheiten nach rechts und eine Längeneinheit nach oben. Du erhältst den Punkt .
Zeichne die Gerade durch die Punkte und .
Du erhältst den Graphen von .
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Funktionsterm der linearen Funktion
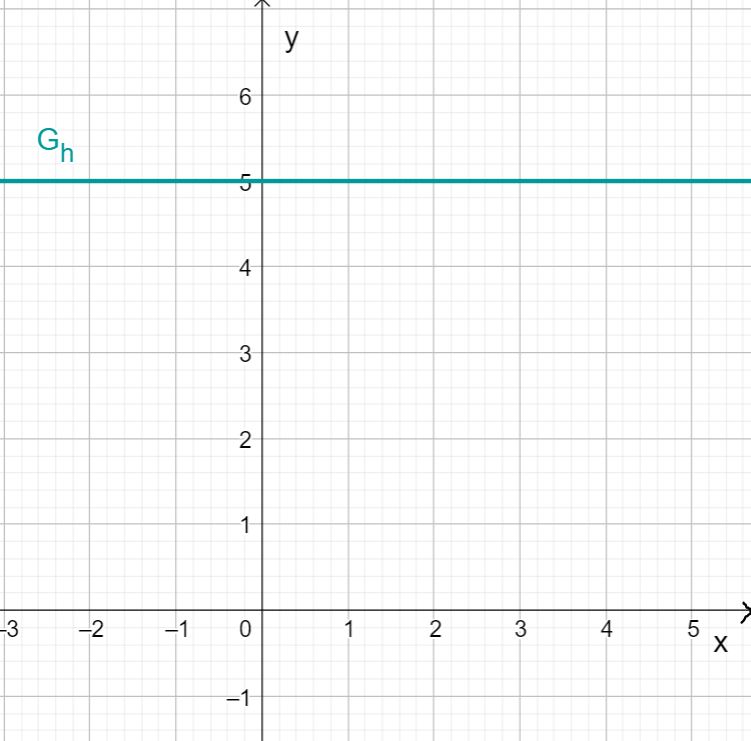
Zeichnen der linearen Funktion
Die Funktion stellt einen Spezialfall der linearen Funktionen dar. Die Steigung von ist gleich .
Das bedeutet, dass sich der Funktionswert unabhängig der Variable nicht ändert.
Wenn du also für jeden Wert den Funktionswert in ein Koordinatensystem einzeichnest erhältst du eine Gerade, die parallel zur -Achse auf der Höhe verläuft.
Hast du eine Frage oder Feedback?
- 3
Zeichne die Graphen der Funktionen mit folgender Funktionsgleichung:
Für diese Aufgabe benötigst Du folgendes Grundwissen: lineare Funktionen
Einen Punkt ermitteln
entspricht der allgemeinen Geradengleichung und ist damit der Schnittpunkt mit der y-Achse .
Steigung ermitteln
Bestimme die Steigung der Funktion
entspricht der allgemeinen Geradengleichung und ist damit die Steigung der Geraden.
Gerade zeichnen
Gehe von dem zuvor ermittelten Punkt eine Einheit nach rechts und 3 nach oben, da m gleich 3 ist. Hier befindet sich ein zweiter Punkt der Funktion.
Verbinde anschließend die beiden Punkte zu einer Geraden.
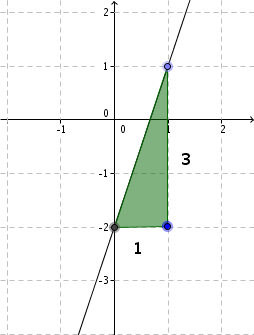
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: lineare Funktionen
Gleichung umstellen
Die Gleichung wird umgestellt, damit sie das Format der allgemeinen Geradengleichung hat.
Einen Punkt ermitteln
entspricht der allgemeinen Geradengleichung und ist damit der Schnittpunkt mit der y-Achse .
Steigung ermitteln
Bestimme nun die Steigung.
entspricht der allgemeinen Geradengleichung und ist damit die Steigung der Geraden.
Gerade zeichnen
Von dem zuvor ermittelten Punkt eine Einheit nach rechts und entsprechend m, nach unten gehen, da m negativ ist. Hier befindet sich ein zweiter Punkt der Funktion .
Anschließend die beiden Punkte zu einer Geraden verbinden.
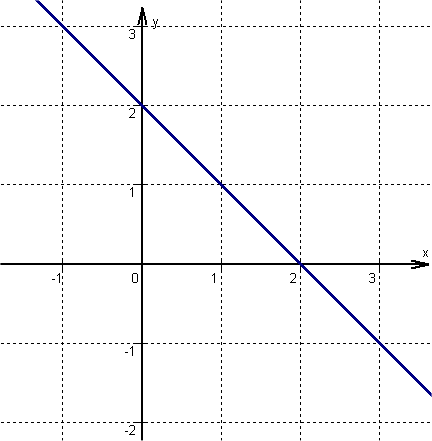
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: lineare Funktionen
Ein Punkt ermitteln
entspricht der allgemeinen Geradengleichung und ist damit der Schnittpunkt mit der y-Achse .
Steigung ermitteln
Bestimme nun die Steigung.
entspricht der allgemeinen Geradengleichung und ist damit die Steigung der Geraden.
Gerade zeichnen
Von dem zuvor ermittelten Punkt eine Einheit nach rechts und entsprechend , nach unten gehen, da m negativ ist. Hier befindet sich ein zweiter Punkt der Funktion.
Anschließend die beiden Punkte zu einer Geraden verbinden.
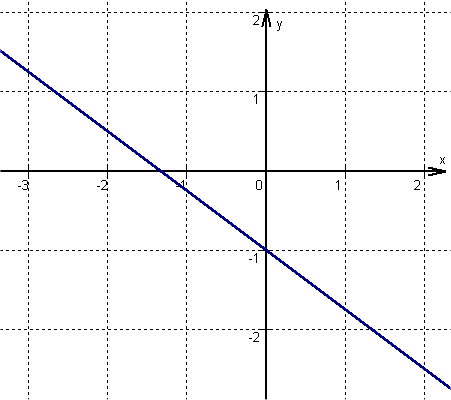
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: lineare Funktionen
Einen Punkt ermitteln
entspricht der allgemeinen Geradengleichung und ist damit der Schnittpunkt mit der y-Achse .
Steigung ermitteln
Bestimme nun die Steigung.
entspricht der allgemeinen Geradengleichung und ist damit die Steigung der Geraden.
Gerade zeichnen
Von dem zuvor ermittelten Punkt eine Einheit nach rechts und entsprechend , nach unten gehen, da m negativ ist. Hier befindet sich ein zweiter Punkt der Funktion .
Anschließend die beiden Punkte zu einer Geraden verbinden.
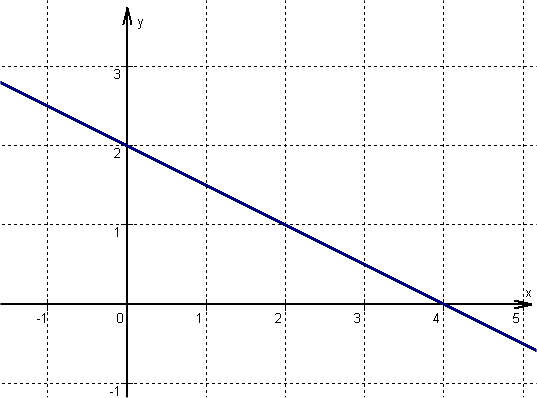
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: lineare Funktionen
Einen Punkt ermitteln
entspricht der allgemeinen Geradengleichung und ist damit der Schnittpunkt mit der y-Achse .
Steigung ermitteln
Bestimme nun die Steigung.
entspricht m der allgemeinen Geradengleichung und ist damit die Steigung der Geraden.
Gerade zeichnen
Von dem zuvor ermittelten Punkt eine Einheit nach rechts und entsprechend m, nach oben gehen, da m positiv ist. Hier befindet sich ein zweiter Punkt der Funktion .
Anschließend die beiden Punkte zu einer Geraden verbinden.
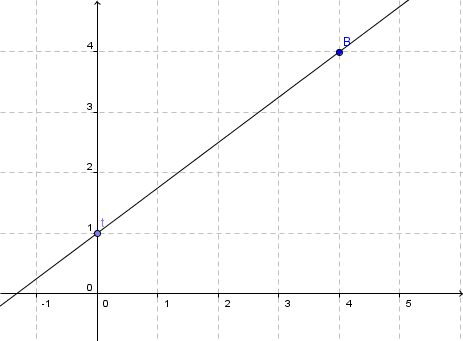
Hast du eine Frage oder Feedback?
- 4
Zeichne die Graphen folgender Geraden mit dem Schnittpunkt mit der y-Achse und dem Steigungsdreieck. Berechne den Schnittpunkt mit der x-Achse und überprüfe das Ergebnis anhand des Graphen.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Gerade im Koordinatensystem
Lies zunächst den y-Achsenabschnitt und die Steigung aus der Funktionsgleichung ab.
Berechne nun den Schnittpunkt mit der x-Achse. Setze dazu den Funktionsterm mit 0 gleich.
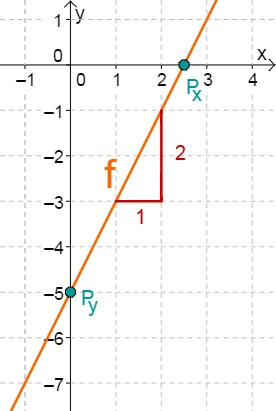
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Gerade im Koordinatensystem
Lies zunächst den y-Achsenabschnitt und die Steigung aus der Funktionsgleichung ab.
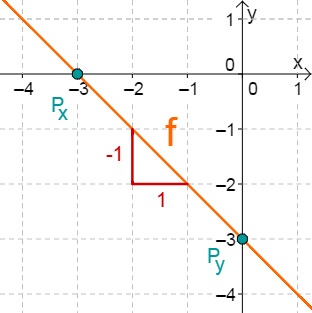
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Gerade im Koordinatensystem
Lies zunächst den y-Achsenabschnitt und die Steigung aus der Funktionsgleichung ab.
Berechne nun den Schnittpunkt mit der x-Achse. Setze dazu den Funktionsterm mit 0 gleich.
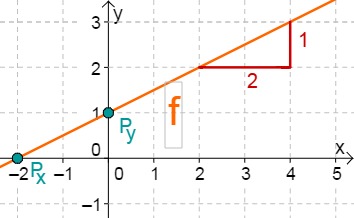
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Gerade im Koordinatensystem
Lies zunächst den y-Achsenabschnitt und die Steigung aus der Funktionsgleichung ab.
Berechne den Schnittpunkt mit der x-Achse. Setze dazu den Funktionsterm mit 0 gleich.
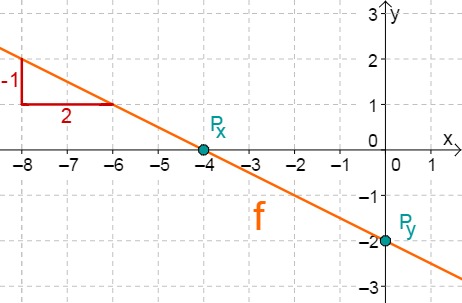
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Gerade im Koordinatensystem
Lies zunächst den y-Achsenabschnitt und die Steigung aus der Funktionsgleichung ab.
Berechne den Schnittpunkt mit der x-Achse. Setze dazu den Funktionsterm mit 0 gleich.
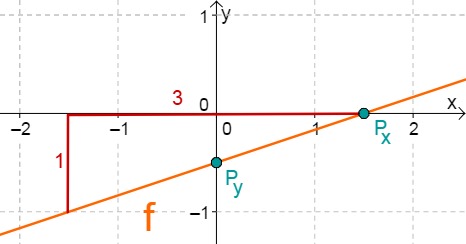
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Gerade im Koordinatensystem
Lies zunächst den y-Achsenabschnitt und die Steigung aus der Funktionsgleichung ab.
Berechne den Schnittpunkt mit der x-Achse. Setze dazu den Funktionsterm mit 0 gleich.
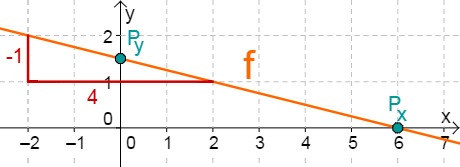
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Gerade im Koordinatensystem
Lies zunächst den y-Achsenabschnitt und die Steigung aus der Funktionsgleichung ab.
Berechne den Schnittpunkt mit der x-Achse. Setze dazu den Funktionsterm mit 0 gleich.
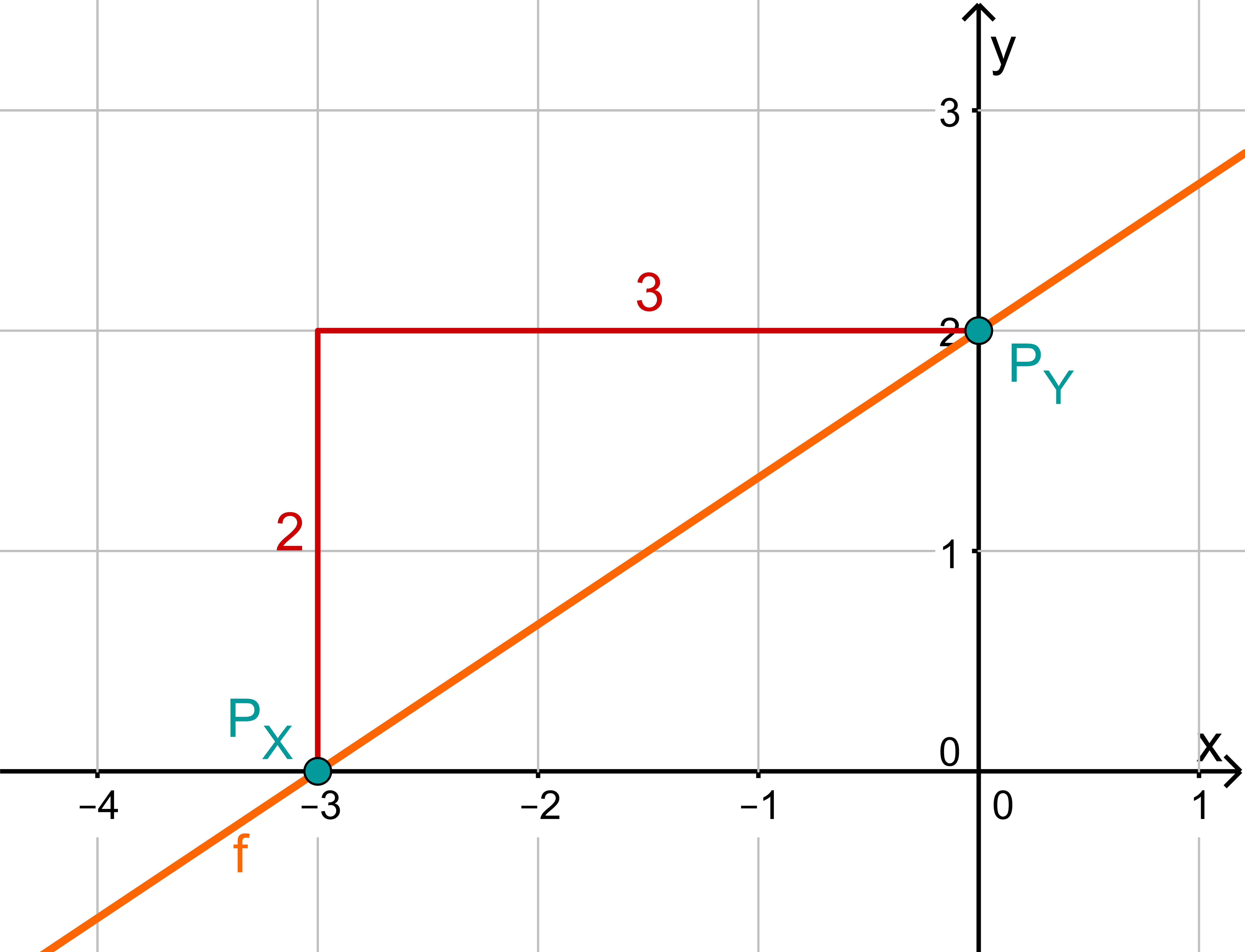
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Gerade im Koordinatensystem
Lies zunächst den y-Achsenabschnitt und die Steigung aus der Funktionsgleichung ab.
Berechne den Schnittpunkt mit der x-Achse. Setze dazu den Funktionsterm mit 0 gleich.
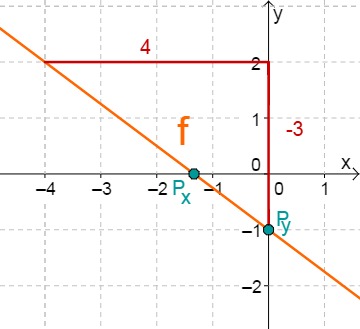
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Gerade im Koordinatensystem
Lies zunächst den y-Achsenabschnitt und die Steigung aus der Funktionsgleichung ab.
Berechne den Schnittpunkt mit der x-Achse. Setze dazu den Funktionsterm mit 0 gleich.
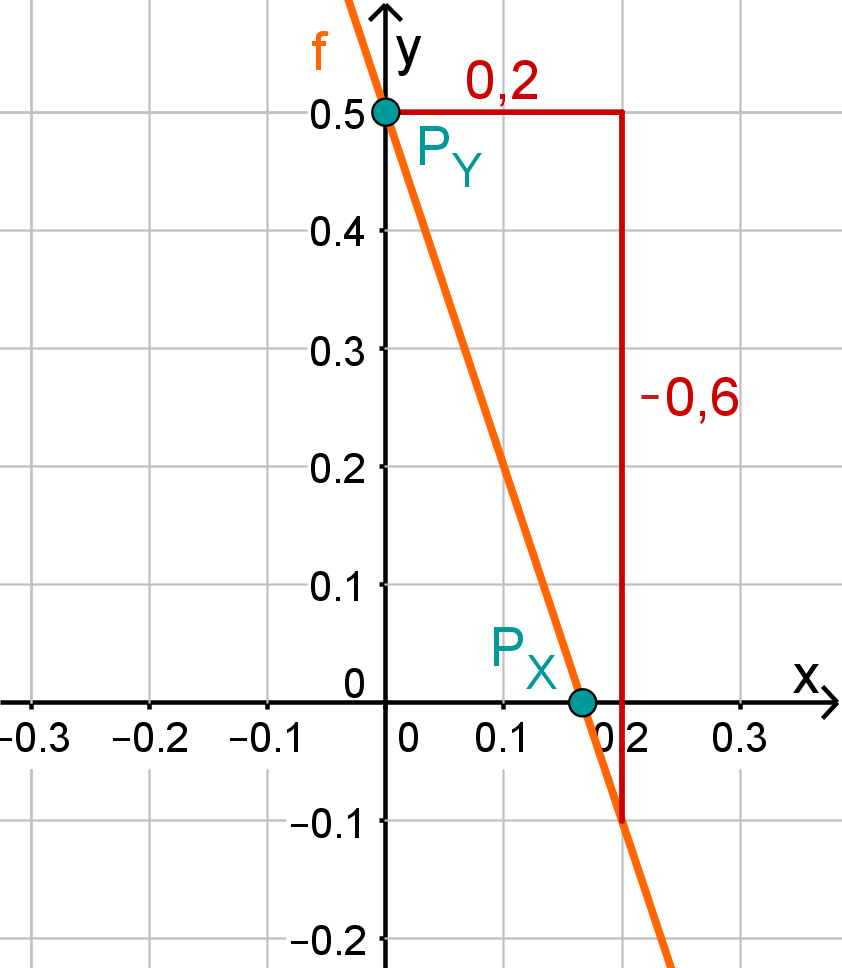
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Gerade im Koordinatensystem
Lies zunächst den y-Achsenabschnitt und die Steigung aus der Funktionsgleichung ab.
Berechne den Schnittpunkt mit der x-Achse. Setze dazu den Funktionsterm mit 0 gleich.
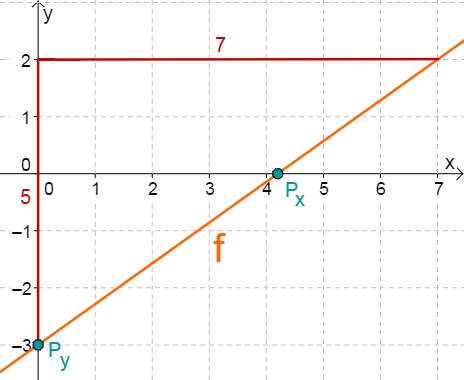
Hast du eine Frage oder Feedback?
- 5
Zeichnen Sie die Graphen folgender Funktionen jeweils in ein Koordinatensystem.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Gerade ins Koordinatensystem zeichnen
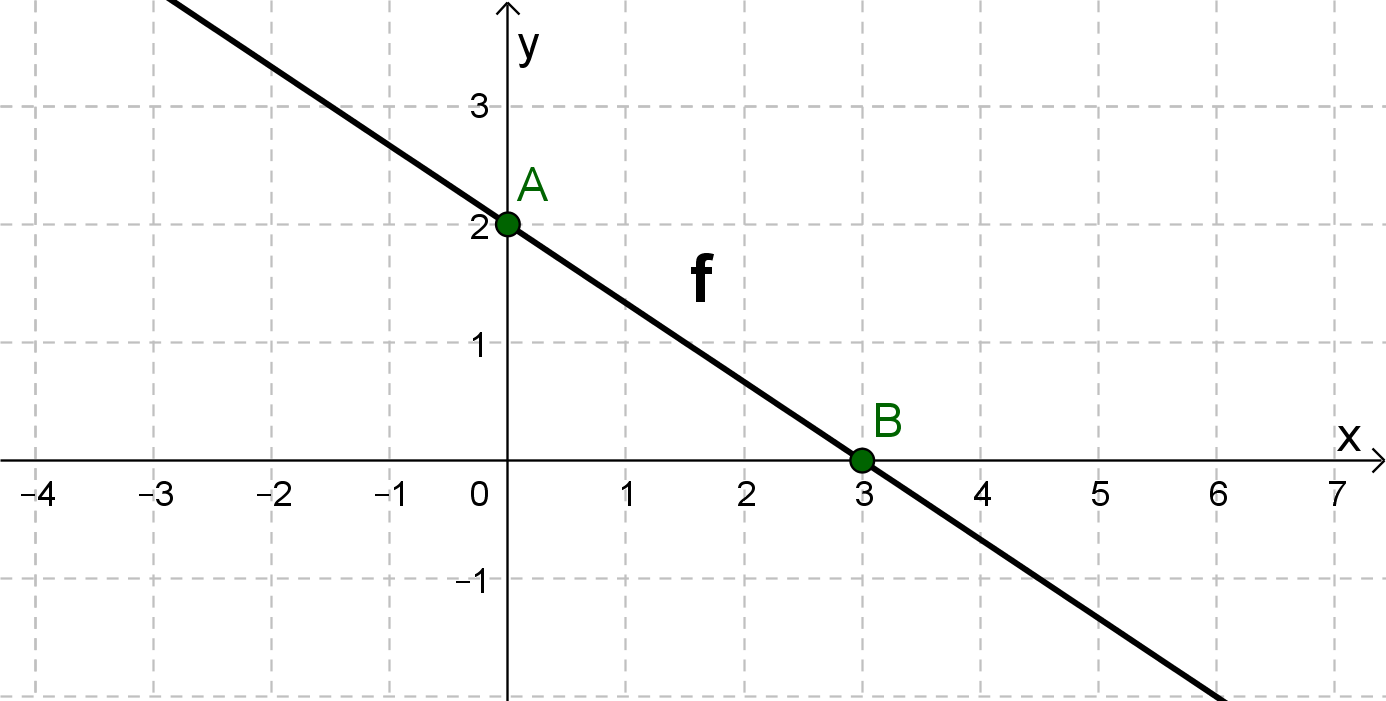
Hast du eine Frage oder Feedback?
Zeichne den y-Achsenabschnitt als Punkt ein (hier A(0|2)).
Gehe entsprechend der Steigung 3 nach rechts und 2 nach unten und zeichne den Punkt ein (hier B(3|0)).
Verbinde die beiden Punkte zu einer Geraden.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Gerade ins Koordinatensystem zeichnen
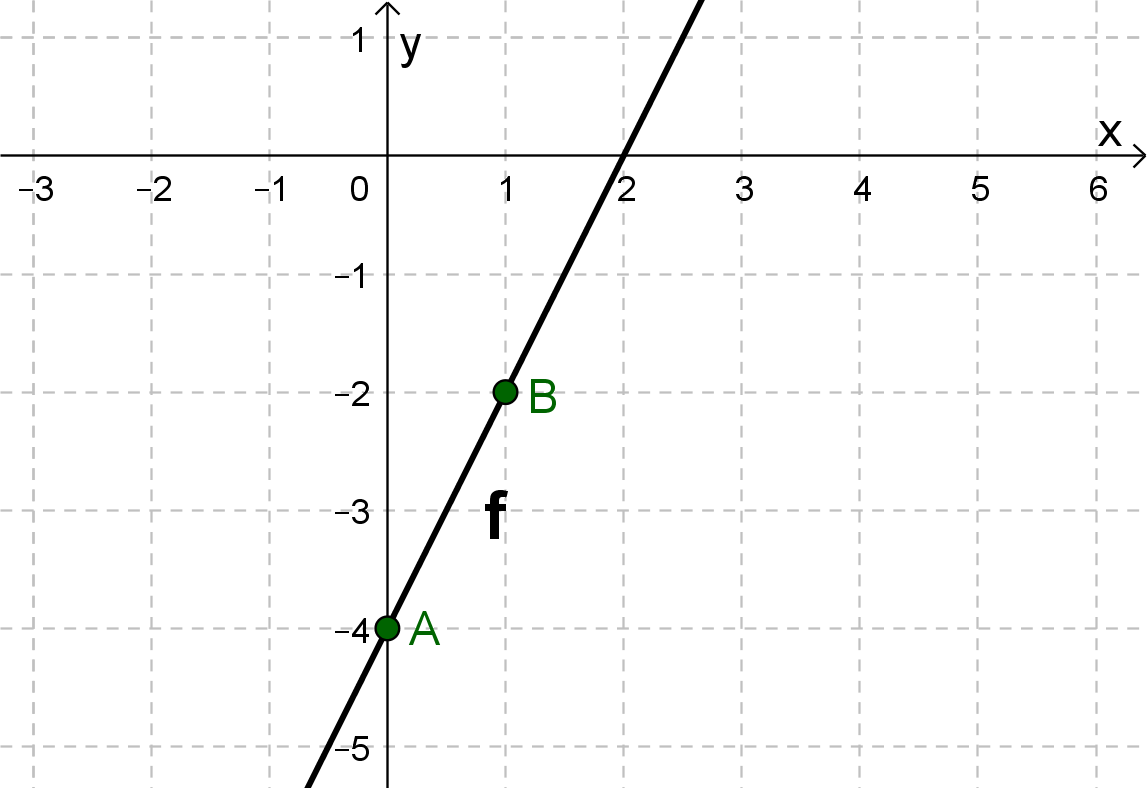
Hast du eine Frage oder Feedback?
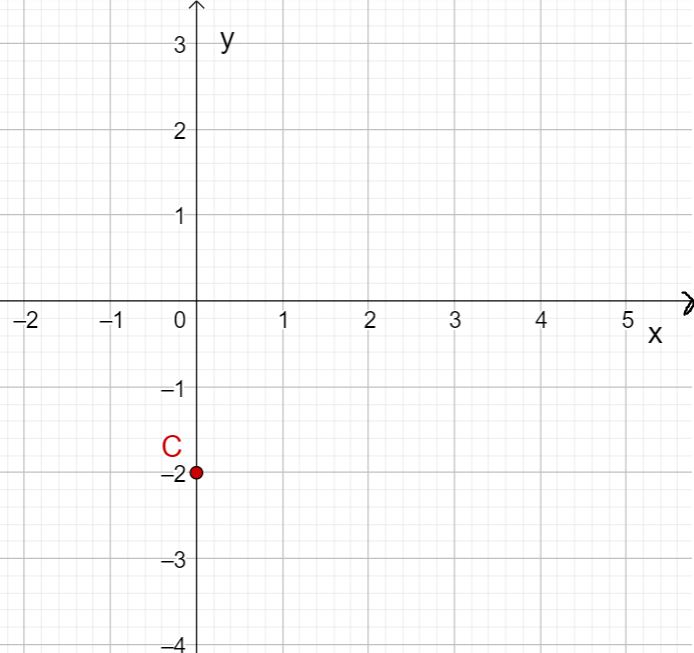
Zeichne den y-Achsenabschnitt als Punkt ein (hier A(0|-4)).
Gehe entsprechend der Steigung 1 nach rechts und 2 nach oben und zeichne den Punkt ein (hier B(1|-2)).
Verbinde die beiden Punkte zu einer Geraden.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Gerade ins Koordinatensystem zeichnen
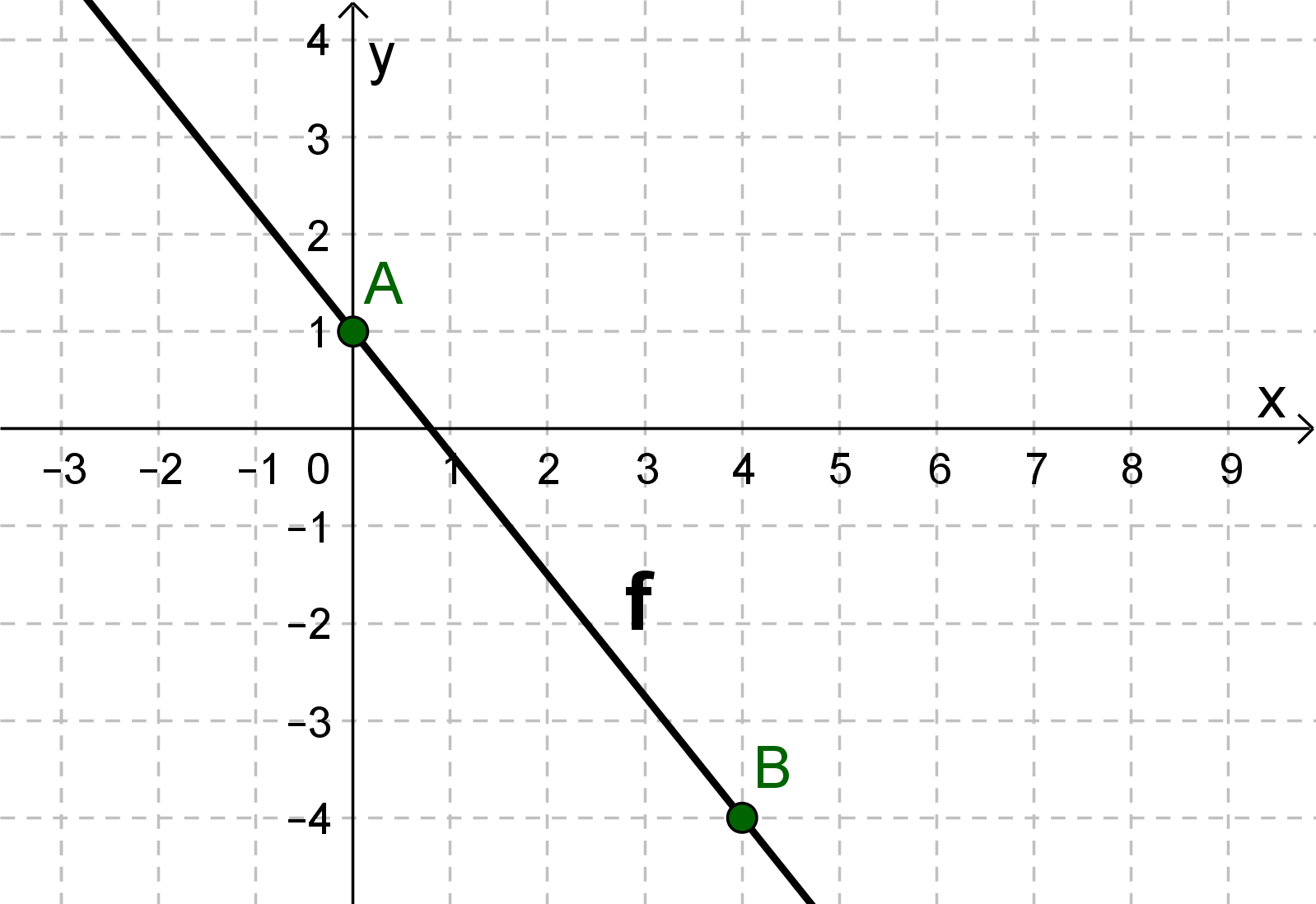
Hast du eine Frage oder Feedback?
Zeichne den y-Achsenabschnitt als Punkt ein (hier A(0|1)).
Gehe entsprechend der Steigung 4 nach rechts und 5 nach unten und zeichne den Punkt ein (hier B(4|-4)).
Verbinde die beiden Punkte zu einer Geraden.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Gerade ins Koordinatensystem zeichnen
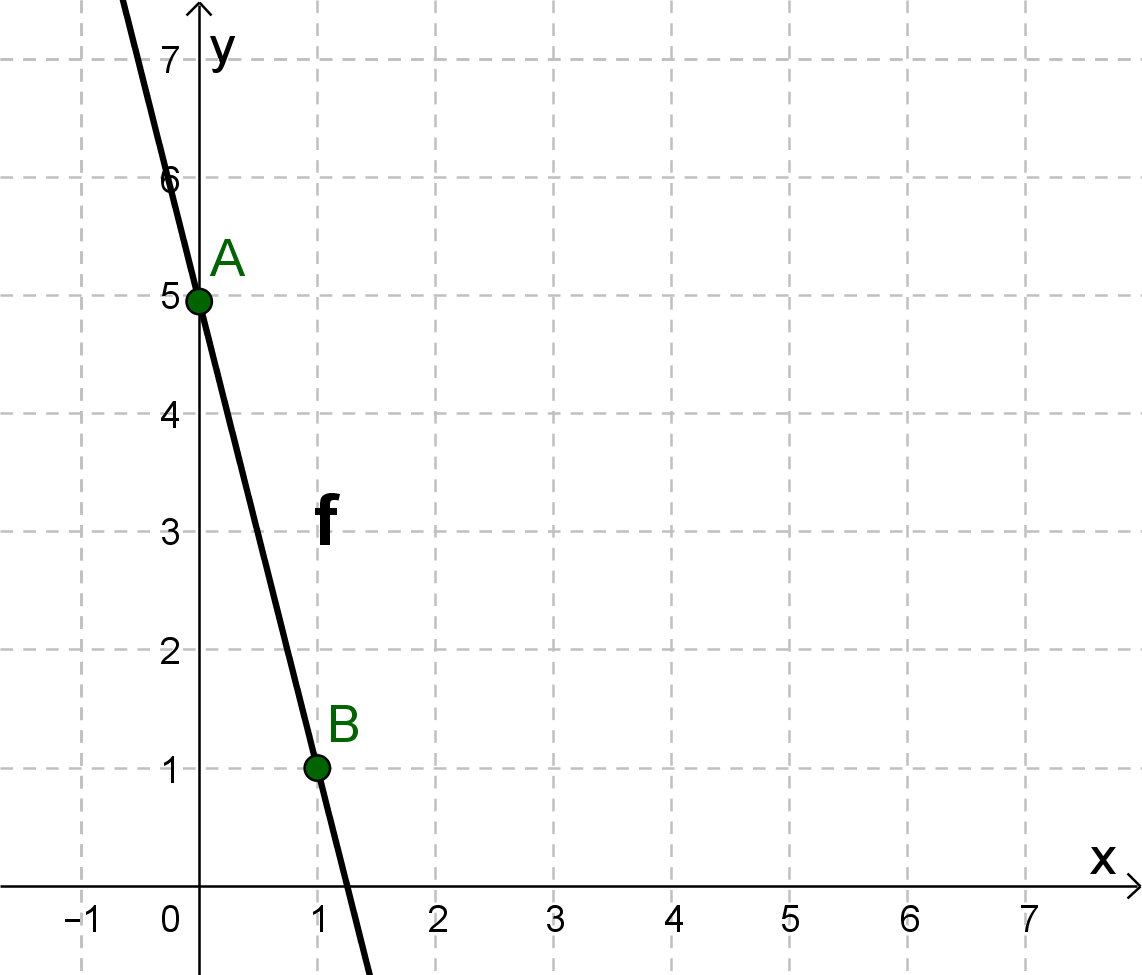
Hast du eine Frage oder Feedback?
Zeichne den y-Achsenabschnitt als Punkt ein (hier A(0|5)).
Gehe entsprechend der Steigung 1 nach rechts und 4 nach unten und zeichne den Punkt ein (hier B(1|1)).
Verbinde die beiden Punkte zu einer Geraden.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Gerade ins Koordinatensystem zeichnen
Hast du eine Frage oder Feedback?
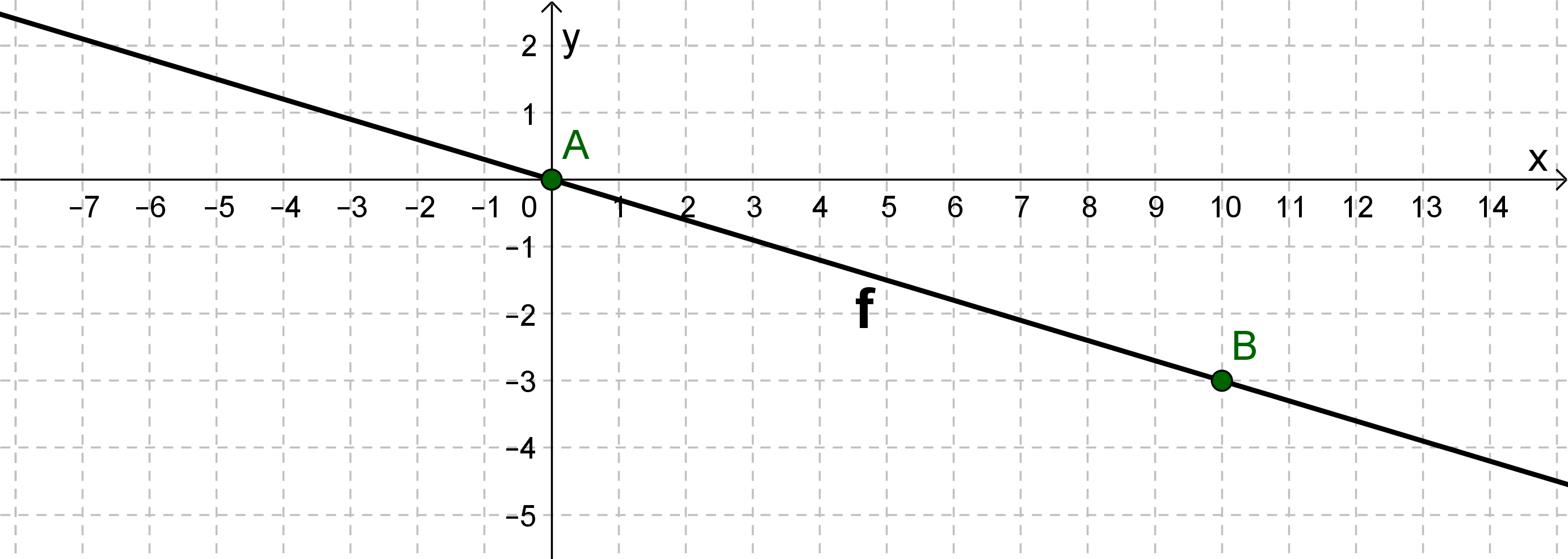
Der Vergleich mit der allgemeinen Form der Geradengleichung , ergibt: Achsenabschnitt und Steigung
Aus dem Wert des y-Achsenabschnitt folgt, dass es sich um eine Ursprungsgerade handelt. Der eine Geradenpunkt ist deshalb der Ursprung: .
Schreibe die Steigung als Bruch: . Gehe entsprechend der Steigung 10 nach rechts und 3 nach unten. Dort ist der zweiten Geradenpunkt .
Die Gerade verläuft durch die beiden Punkte und .
Für diese Aufgabe benötigst Du folgendes Grundwissen: Gerade ins Koordinatensystem zeichnen
Der y-Wert der Gerade ist immer 2,5. Darum ist die Gerade eine Parallele zur x-Achse.

Hast du eine Frage oder Feedback?
- 6
Gegeben ist die Funktion mit .
Tabellarisiere die Funktion für mit der Schrittweite .
Für diese Aufgabe benötigst Du folgendes Grundwissen: Lineare Funktion
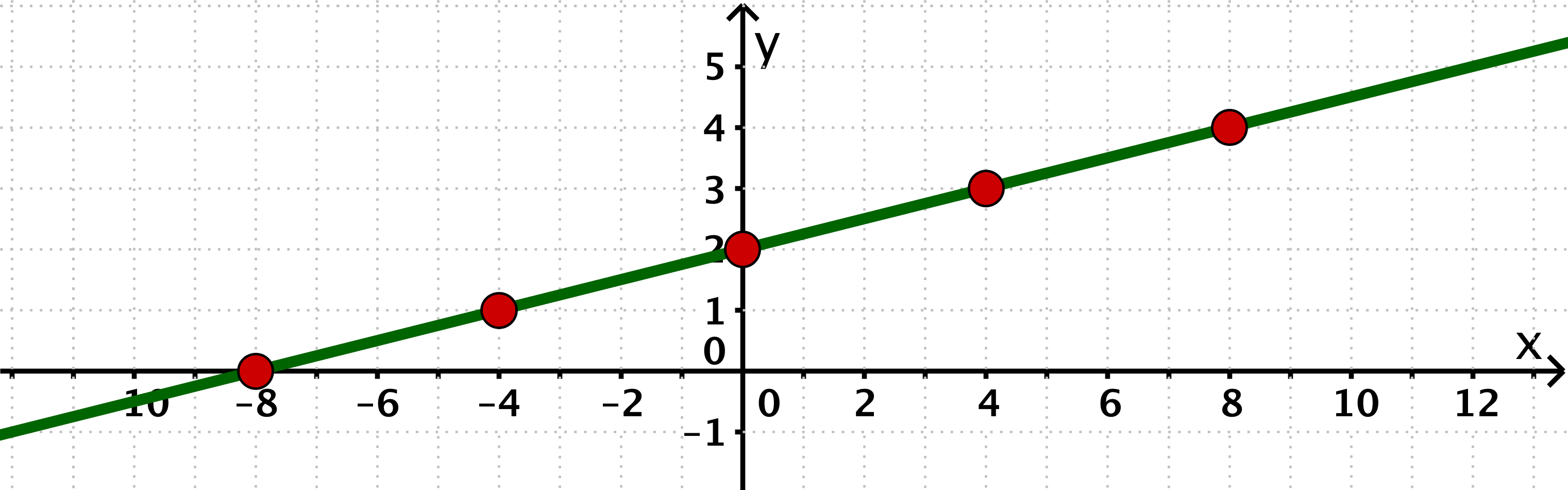
Wertetabelle zu mit der Schrittweite :

Hast du eine Frage oder Feedback?
Trage die Punkte der Funktion in ein Koordinatensystem ein und zeichne den Graphen der Funktion .
Für diese Aufgabe benötigst Du folgendes Grundwissen: Lineare Funktion
Punkte der Funktion im Koordinatensystem und Graph der Funktion :
Hast du eine Frage oder Feedback?
Zu welcher besonderen Art von Geraden gehört der Graph der Funktion ?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Lineare Funktion
Der Graph der Funktion ist eine Gerade, die durch den Ursprung des Koordinatensystems verläuft. Sie wird deshalb auch Ursprungsgerade genannt.
Hast du eine Frage oder Feedback?
Überprüfe rechnerisch, ob die Punkte und auf dem Graphen der Funktion liegen.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Lineare Funktion
Setze die Koordinaten von und in die Funktionsgleichung ein:
Punkt :
↓ Koordinaten einsetzen
↓ falsche Aussage
Antwort: Der Punkt liegt nicht auf dem Graphen der Funktion .
Punkt :
↓ Koordinaten einsetzen
↓ wahre Aussage
Antwort: Der Punkt liegt auf dem Graphen der Funktion .
Zusätzliche Veranschaulichung des Graphens mit den beiden Punkten und
Nicht in der Aufgabenstellung gefordert.
Hast du eine Frage oder Feedback?
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?