Aufgaben zu Graphen von linearen Funktionen

Zeichne den Graphen der linearen Funktionen in ein Koordinatensystem ein!

$f (x) = - 2 x + 4$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Funktionsterm linearer Funktionen
Zeichnen der linearen Funktion
Lese zunächst $y$ -Achsenabschnitt und die Steigung aus dem Funktionsterm der linearen Funktion ab.
In diesem Fall:
$f (x) = - 2 x + 4$
Du erhältst für den $y$ -Achsenabschnitt $t = 4$ und für die Steigung $m = - 2$ .
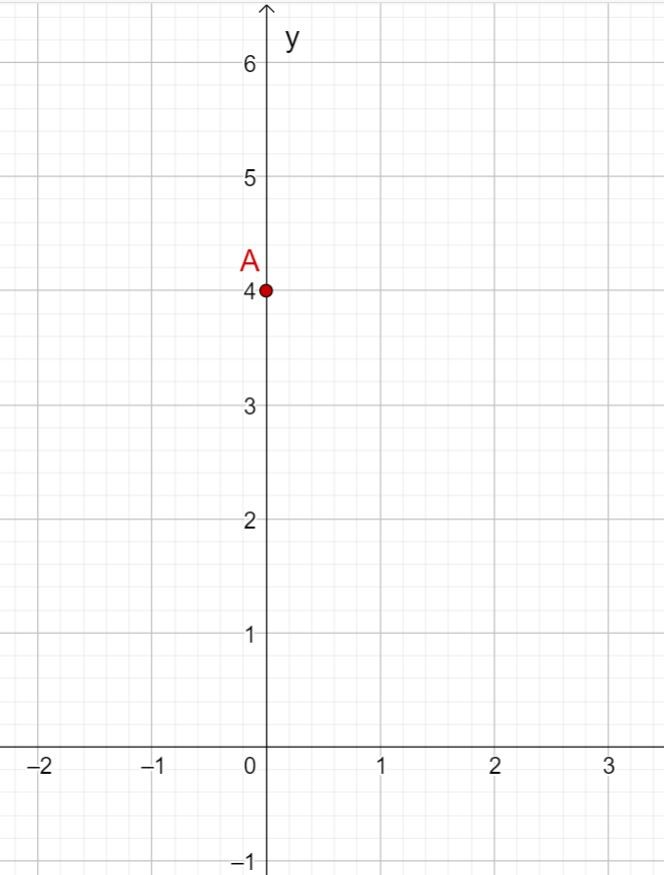
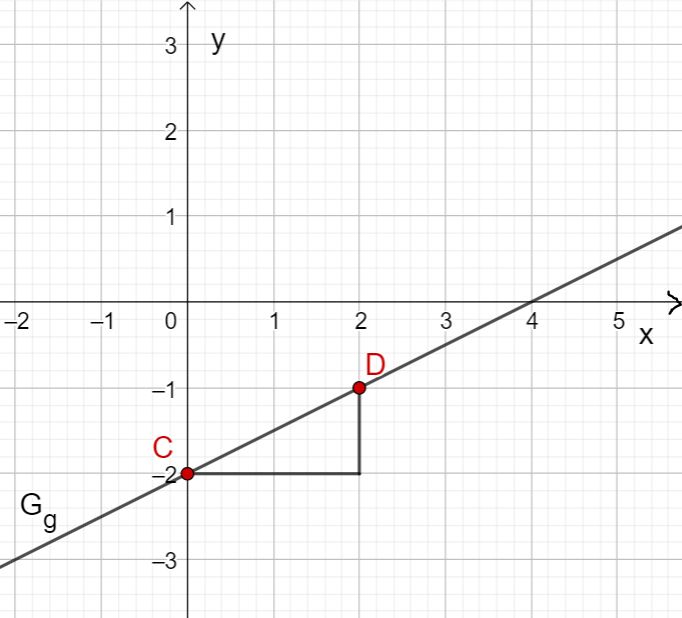
Zeichne zuerst den Schnittpunkt mit der $y$ -Achse ein, der sich durch den $y$ -Achsenabschnitt ergibt. Dieser lautet also $A (0 / 4)$ .
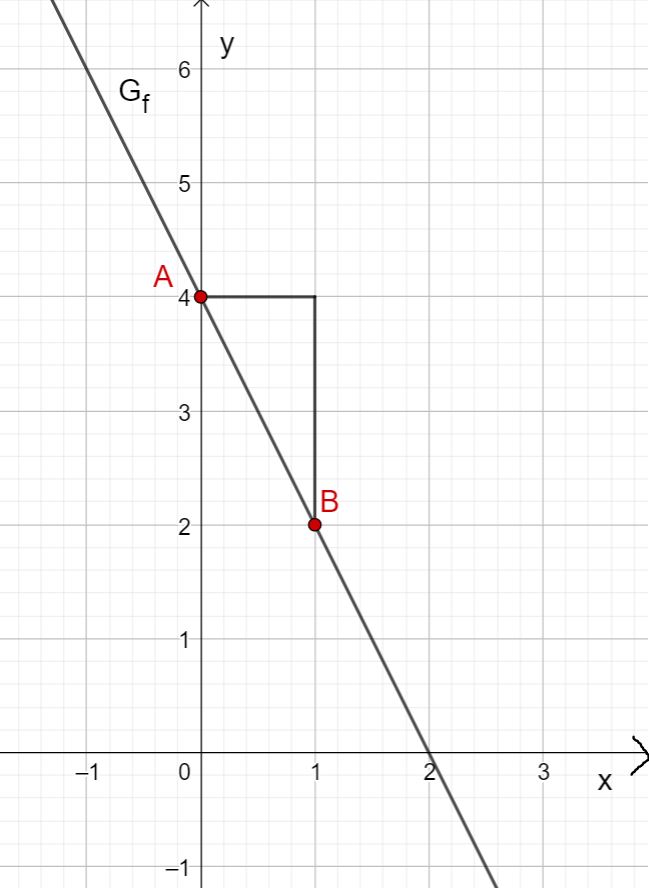
Zeichne anschließend mithilfe der Steigung ein Steigungsdreieck. Gehe dafür eine Längeneinheit nach rechts und zwei Längeneinheiten nach unten. Dadurch erhältst du den Punkt $B = (1 / 2)$ . Ziehe nun die Gerade durch die Punkte $A$ und $B$ .
Du erhältst den Graphen $G_{f}$ von $f (x)$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
$g (x) = \frac{1}{2} x - 2$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Funktionsterm der linearen Funktion
Zeichnen der linearen Funktion
Lese zunächst $y$ -Achsenabschnitt und die Steigung aus dem Funktionsterm der linearen Funktion ab.
In diesem Fall:
$f (x) = \frac{1}{2} x - 2$
Du erhältst für den $y$ -Achsenabschnitt $t = - 2$ und für die Steigung $m = \frac{1}{2}$ .
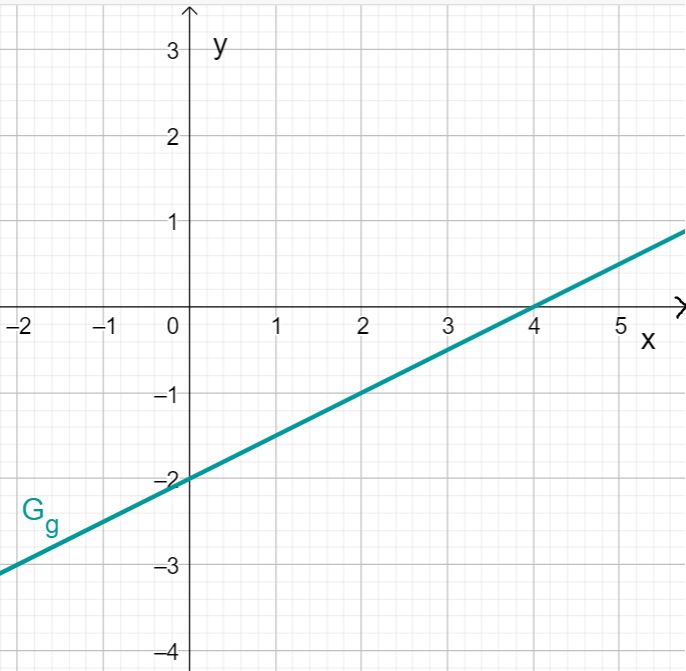
Zeichne zuerst den Schnittpunkt mit der $y$ -Achse ein, der sich durch den $y$ -Achsenabschnitt ergibt. Dieser lautet also $C (0 / - 2)$ .
Zeichne anschließend mithilfe der Steigung ein Steigungsdreieck. Gehe dafür zwei Längeneinheiten nach rechts und eine Längeneinheit nach oben. Du erhältst den Punkt $D = (2 / - 1)$ .
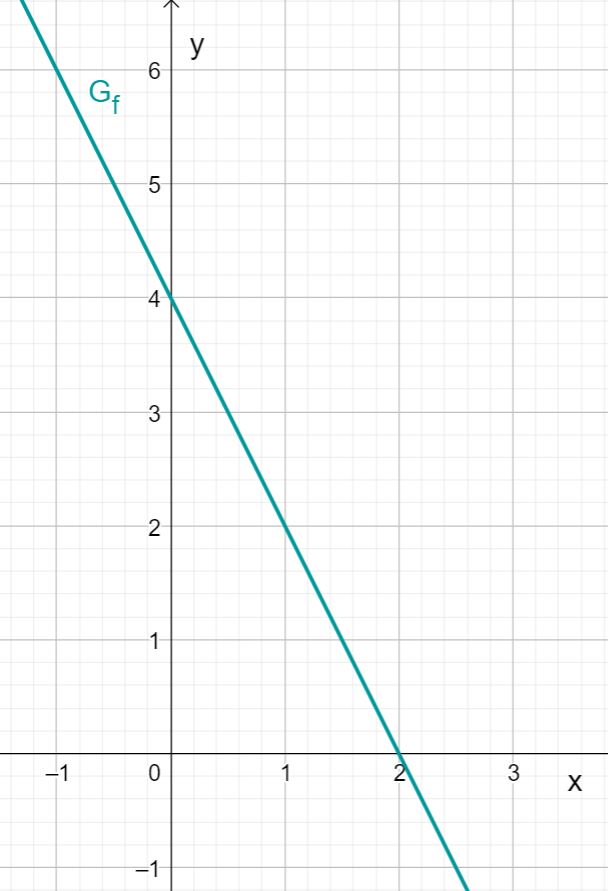
Zeichne die Gerade durch die Punkte $C$ und $D$ .
Du erhältst den Graphen $G_{g}$ von $g (x)$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
$h (x) = 5$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Funktionsterm der linearen Funktion
Zeichnen der linearen Funktion
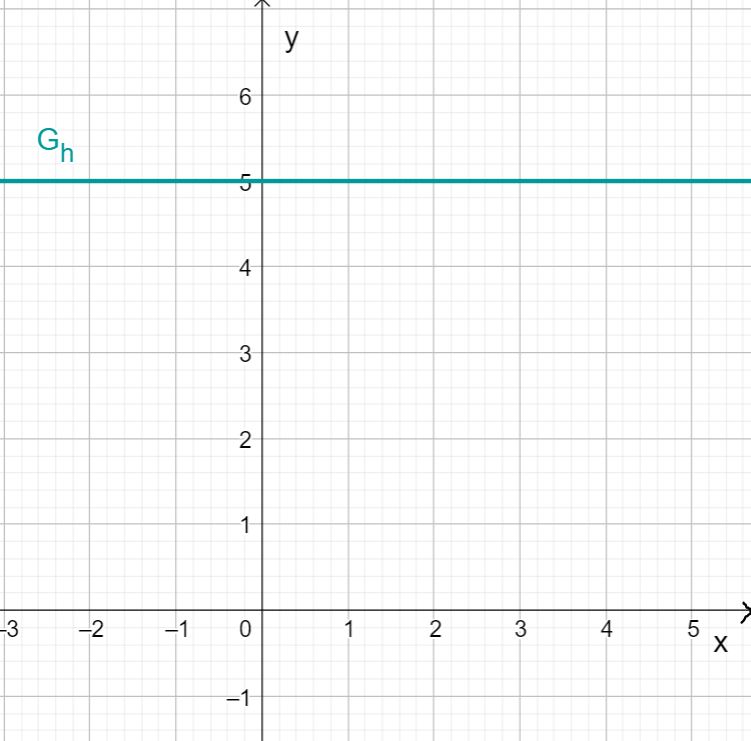
Die Funktion $h (x) = 5$ stellt einen Spezialfall der linearen Funktionen dar. Die Steigung von $h (x)$ ist gleich $0$ .
Das bedeutet, dass sich der Funktionswert unabhängig der Variable $x$ nicht ändert.
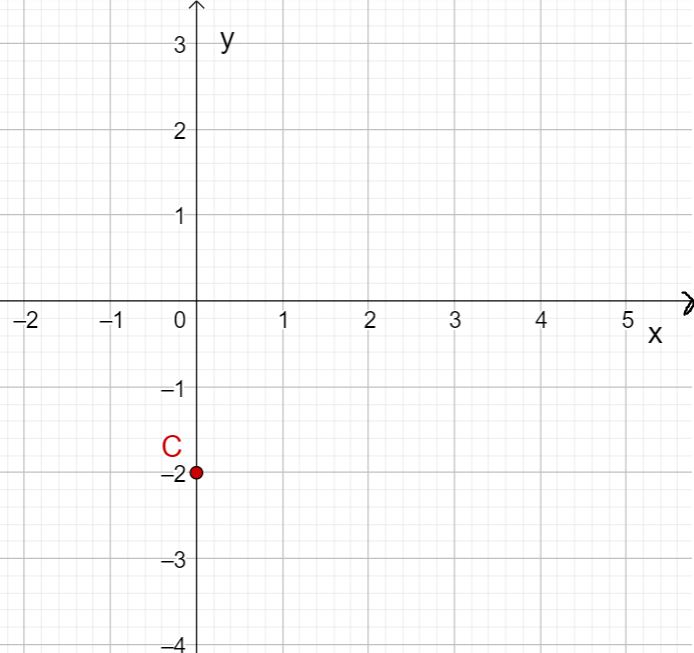
Wenn du also für jeden $x$ Wert den Funktionswert $h (x) = 5$ in ein Koordinatensystem einzeichnest erhältst du eine Gerade, die parallel zur $x$ -Achse auf der Höhe $y = 5$ verläuft.
Hast du eine Frage oder Feedback?
Kommentiere hier 👇