Rechnung mit Vektoren (Vektoren in der Ebene II)

1 Übersicht

Inhalt des Kurses

Du weißt bereits, was Vektoren sind. In diesem Kurs lernst du nun, wie man mit ihnen rechnet. Es werden wichtige Begriffe wie Vektorkette oder Skalarmultiplikation eines Vektors eingeführt. Außerdem lernst du, wie du Vektoren addierst oder subtrahierst.

Vorkenntnisse

Du solltest wissen, was ein Vektor ist. Dies wird im Kurs Vektoren in der Ebene I erklärt.

Kursdauer

weniger als eine Stunde

2 Addition (1/2)

Addition auf der Schatzkarte

Gibt es einen Vektor, der den direkten Weg vom Felsen zum Baum beschreibt? Also eine Möglichkeit, ohne den Umweg über den Wegweiser, der auf der Schatzkarte eingezeichnet wurde, zu dem Baum zu gelangen?

Ja, denn: Du kannst einfach vom Felsen direkt zum Baum gehen. Wenn du beim Felsen beginnst, ist es egal, ob du erst zum Wegweiser und dann zum Baum oder gleich zum Baum gehst. Beide Wege führen zu dem Baum.

Das Ziel, an dem du ankommst, bleibt gleich.

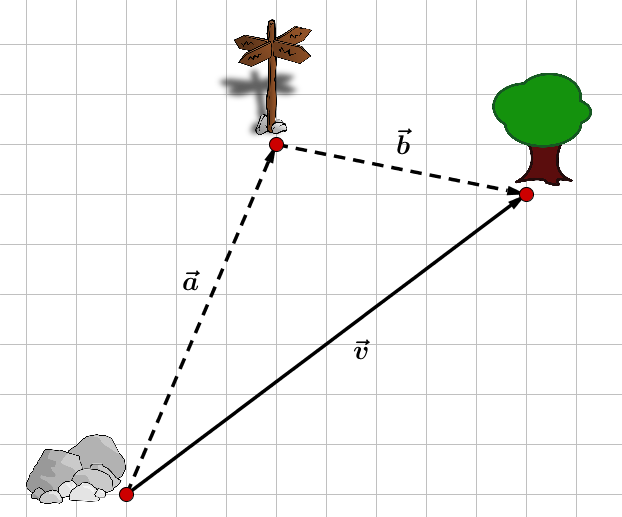
Hängt man also die Vektoren $\vec a$ und $\vec b$ aneinander, führt das zu demselben Punkt wie auch der Vektor $\vec v$ .

Man kann zwei Vektoren aneinanderhängen, indem man sie addiert:

\displaystyle \ \ \ \ \ \vec a + \vec b = \vec v.

3 Addition (2/2)

Die Addition von zwei Vektoren erfolgt komponentenweise, das heißt man zählt $\vec a$ und $\vec b$ zusammen, indem man ihre Koordinaten addiert.

Allgemein

Gegeben: $\ \ \vec a = \begin{pmatrix} a_1 \\ a_2 \end{pmatrix}, \ \ \vec b = \begin{pmatrix} b_1 \\ b_2 \end{pmatrix}.$

Gesucht: $\ \ \vec a + \vec b.$

Lösung: $\ \ \vec a + \vec b = \begin{pmatrix} a_1 \\ a_2 \end{pmatrix} + \begin{pmatrix} b_1 \\ b_2 \end{pmatrix} = \begin{pmatrix} a_1+b_1 \\ a_2+b_2 \end{pmatrix}$

Veranschaulichung:

Beispiel

Gegeben: $\ \ \vec a = \begin{pmatrix} 3 \\ 7 \end{pmatrix}, \ \ \vec b = \begin{pmatrix} 5 \\ -1 \end{pmatrix}.$

Gesucht: $\ \ \vec a + \vec b.$

Lösung: $\ \ \vec a + \vec b = \begin{pmatrix} 3 \\ 7 \end{pmatrix} + \begin{pmatrix} 5 \\ -1 \end{pmatrix} = \begin{pmatrix} 3 + 5 \\ 7 - 1 \end{pmatrix} = \begin{pmatrix} 8 \\ 6 \end{pmatrix}$

Veranschaulichung:

4 Kommutativität der Addition

Bei der Addition von Zahlen darf man laut dem Kommutativgesetz die Summanden vertauschen. Dies wendet man nun auf die Lösung der letzten Kursseite an. In der rechten Spalte werden weiterhin dieselben Rechenschritte am Beispiel durchgeführt.

$\ \ \vec a + \vec b = \begin{pmatrix} x_a + x_b \\ y_a + y_b \end{pmatrix} = \begin{pmatrix} x_b + x_a \\ y_b + y_a \end{pmatrix}$

$\ \ \vec a + \vec b = \begin{pmatrix} 3 + 5 \\ 7 + (-1) \end{pmatrix} = \begin{pmatrix} 5 + 3 \\ -1 + 7 \end{pmatrix}$

Löst man dies nun wieder nach $\vec{a}$ und $\vec{b}$ auf, sieht man, dass man auch bei der Vektoraddition die beiden Summanden vertauschen darf.

$\ \ \begin{pmatrix} x_b + x_a \\ y_b + y_a \end{pmatrix} = \begin{pmatrix} x_b\\ y_b \end{pmatrix} + \begin{pmatrix} x_a \\ y_a \end{pmatrix} = \vec b + \vec a$

$\ \ \begin{pmatrix} 5 + 3 \\ -1 + 7 \end{pmatrix} = \begin{pmatrix} 5 \\ -1 \end{pmatrix} + \begin{pmatrix} 3 \\ 7 \end{pmatrix} = \vec b + \vec a$

Es gilt also auch hier das Kommutativgesetz:

\displaystyle \vec a + \vec b = \vec b + \vec a

5 Aufgaben zur Addition

Laden

6 Subtraktion (1/2)

Jetzt hast du schon gelernt, wie man Vektoren miteinander addiert. Die Subtraktion funktioniert im Grunde ähnlich.

Die Subtraktion von zwei Vektoren erfolgt komponentenweise, das heißt man zieht $\vec b$ von $\vec c$ ab, indem man ihre Koordinaten subtrahiert.

Man schreibt:

\displaystyle \vec a = \vec c - \vec b

Komponentenweise, mit $\vec c = \begin{pmatrix}x_c\\y_c\end{pmatrix}$ und $\vec b = \begin{pmatrix}x_b\\y_b\end{pmatrix}$ :

\displaystyle \vec c - \vec b = \begin{pmatrix}x_c\\y_c\end{pmatrix} - \begin{pmatrix}x_b\\y_b\end{pmatrix} = \begin{pmatrix}x_c-x_b\\y_c-y_b\end{pmatrix}

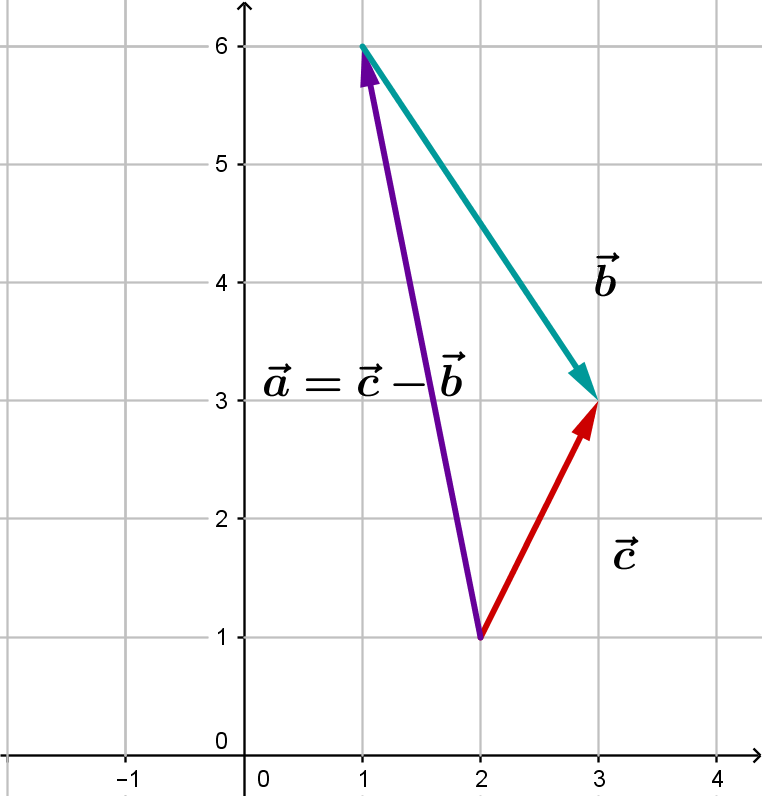
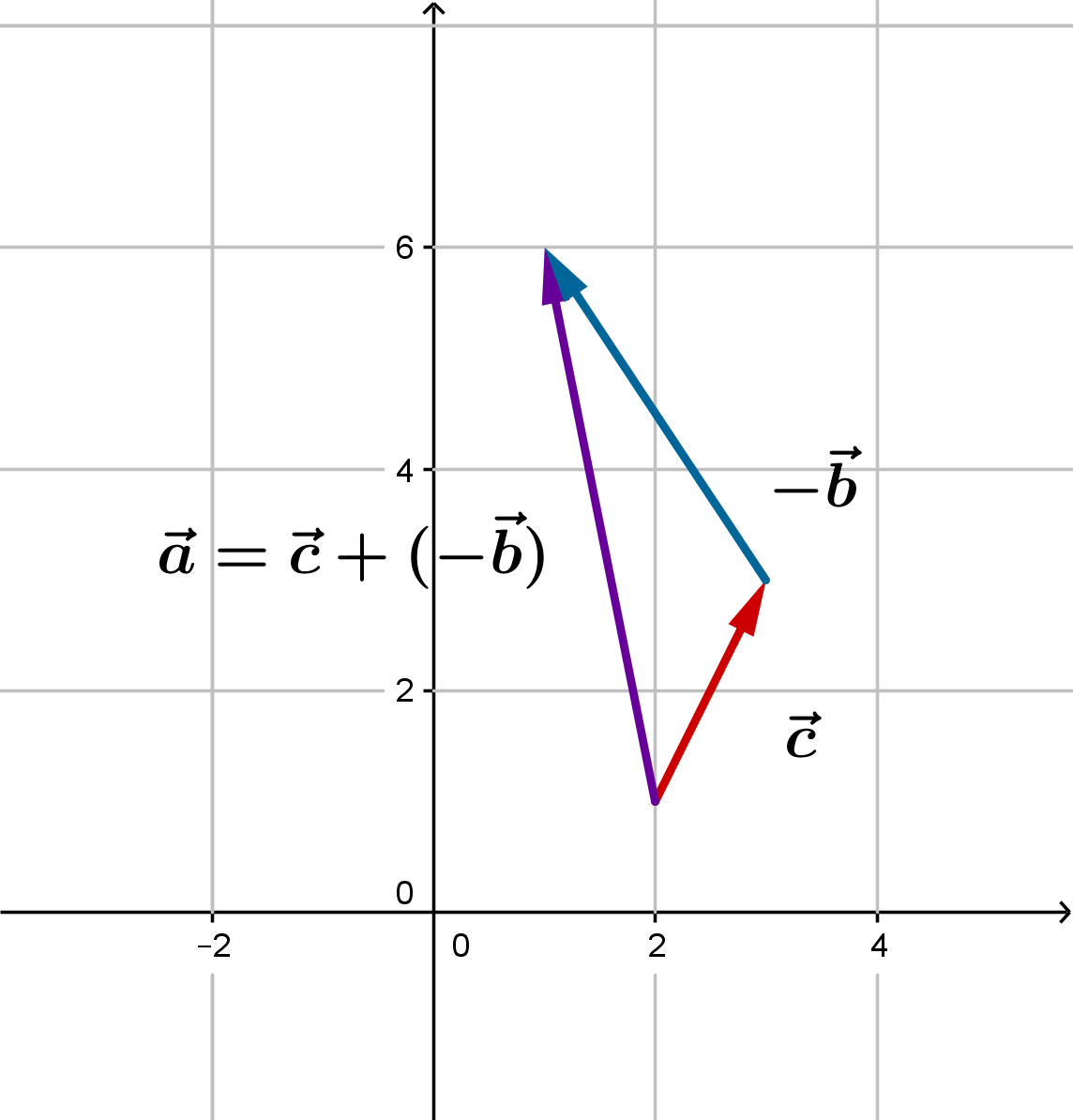
Anschaulich kann man sich diese Subtraktion so vorstellen, dass man den Gegenvektor addiert.

\displaystyle \vec c + (-\vec b) = \begin{pmatrix}x_c\\y_c\end{pmatrix} + \begin{pmatrix}-x_b\\-y_b\end{pmatrix} = \begin{pmatrix}x_c-x_b\\y_c-y_b\end{pmatrix}

7 Subtraktion (2/2)

Beispiel

Man hat die Vektoren

$\vec v = \begin{pmatrix}-3\\7\end{pmatrix}$ und $\,\vec w = \begin{pmatrix}-6\\2\end{pmatrix}\,$ gegeben.

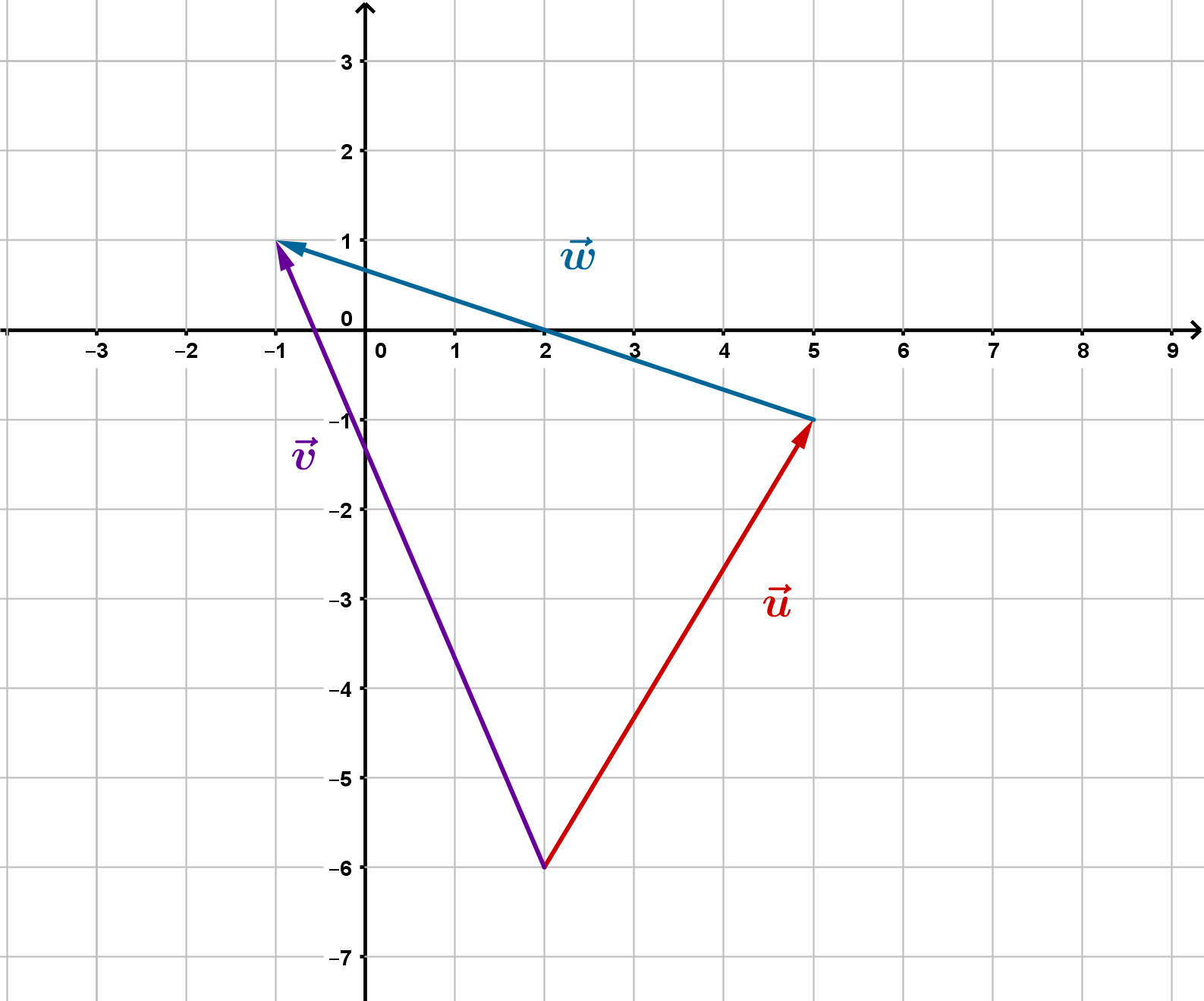
Du sollst nun die Vektorsubtraktion von $\vec v$ und $\vec w$ bestimmen. Bilde also die Differenz:

$\overrightarrow u=\overrightarrow v-\overrightarrow w=\begin{pmatrix}-3\\7\end{pmatrix}-\begin{pmatrix}-6\\2\end{pmatrix}=\begin{pmatrix}-3-(-6)\\7-2\end{pmatrix}=\begin{pmatrix}3\\5\end{pmatrix}$

Wie das geometrisch aussieht, siehst du im Bild rechts.

8 Aufgaben zur Subtraktion

Laden

9 Skalarmultiplikation

Man kann Vektoren nicht nur addieren und subtrahieren, sondern auch strecken oder stauchen, d.h. "länger oder kürzer machen". Dies versteht man unter einer Skalarmultiplikation, also der Multiplikation von einem Vektor und einer beliebigen reellen Zahl.

Mathematisch schreibt man das folgendermaßen:

$\vec w = k \cdot \vec v$ , wobei $\ k \in \mathbb{R}\,$ .

Die Richtung des Vektors verändert sich bis auf das Vorzeichen dabei nicht.

Beispiel

Du hast den Vektor $\vec v = \begin{pmatrix}2\\-3 \end{pmatrix}$ gegeben und möchtest ihn um $7$ strecken, also:

$\vec w = k \cdot \vec v = 7 \cdot \begin{pmatrix}2\\-3 \end{pmatrix} = \begin{pmatrix} 7 \cdot 2\\ 7 \cdot (-3) \end{pmatrix} = \begin{pmatrix} 14 \\ -21 \end{pmatrix}$

Der gestreckte Vektor ist nun also $\vec w = \begin{pmatrix} w_1 \\ w_2 \end{pmatrix} = \begin{pmatrix} 14\\-21\end{pmatrix}$ .

$\,$

Nun kann man andersrum aber auch nachrechnen, ob ein Vektor $\vec w$ aus $\vec v$ hervorgeht. D.h., wenn man den Vektor $\vec v = \begin{pmatrix} v_1 \\ v_2 \end{pmatrix}$ gegeben hat und der Vektor $\vec w = \begin{pmatrix} w_1 \\ w_2 \end{pmatrix}$ aus der Multiplikation von $k$ mit $v$ hervorgeht. Dazu untersucht man, ob der Vektor $\vec w$ aus der Multiplikation von $k$ und $\vec v = \begin{pmatrix} v_1 \\ v_2\end{pmatrix}$ hervorgeht:

$\begin{pmatrix}k \cdot v_1 \\ k \cdot v_2 \end{pmatrix} = \begin{pmatrix} w_1 \\ w_2 \end{pmatrix}$

$\Longleftrightarrow$

$k \cdot v_1 = w_1$

$k \cdot v_2 = w_2$

Dann muss man für sowohl für die $x$ - als auch für die $y$ -Komponente den Wert für $k$ nachrechnen:

\displaystyle k=\frac{w_1}{v_1}

\displaystyle k = \frac{w_2}{v_2}

Wenn man für beide Gleichungen denselben Wert für $k$ bekommt, so geht $\vec w$ aus $\vec v$ hervor.

Falls man jedoch unterschiedliche Werte ausrechnet, so geht keiner der beiden Vektoren aus dem anderen hervor.

Beispiel

Prüfe nach, ob sich der Vektor $\vec w = \begin{pmatrix}-12\\16\end{pmatrix}$ durch Streckung des Vektors $\vec v = \begin{pmatrix} 3\\-4\end{pmatrix}$ darstellen lässt.

Du musst also untersuchen, ob sich $\vec w$ als $k \cdot \vec v\,$ schreiben lässt.

$\vec w = k \cdot \vec v\,\,$ $\Longleftrightarrow$ $\begin{pmatrix}-12\\16\end{pmatrix} = k \cdot \begin{pmatrix}3\\-4\end{pmatrix}$

Du musst nun also den Wert von $k$ sowohl für die $x$ -als auch für die $y$ -Koordinate bestimmen

Für die $x$ -Komponente gilt:

$-12 = 3k\,\,\Longleftrightarrow k = -4$

Für die $y$ -Komponente gilt:

$16 = -4k\,\,\Longleftrightarrow k = -4$

$\,$

Für beide Komponenten bekommst du also das gleiche Ergebnis heraus.

Damit lässt sich der Vektor $\vec w$ durch Streckung von $\vec v$ mit dem Faktor $- 4$ erzeugen!

Unten kannst du in dem Applet sehen, wie sich die Darstellung von Vektoren im Koordinatensystem ändert, wenn man die Vektoren streckt oder staucht.

Bewege den blauen Punkt an der Spitze des Vektors $\vec{v}$ , um verschiedene Vektoren $\vec{v}$ zu betrachten. Verschiebe den roten Punkt k auf dem Schieberegler, um den Vektor $\vec{v}$ um den Faktor k zu strecken oder zu stauchen. Der rote Vektor $\vec{w}$ stellt dann den gestreckten bzw. gestauchten Vektor $\vec{w}=k\cdot\vec{v}$ dar.

Mit einem Klick auf Bild oder Button oben stimmst du zu, dass externe Inhalte von GeoGebra geladen werden. Dabei können persönliche Daten zu diesem Service übertragen werden – entsprechend unserer Datenschutzerklärung.

[https://www.geogebra.org/material/iframe/id/1583451]

10 Aufgaben zur Skalarmultiplikation

Laden

11 Vektorkette

Durch Kombination der Operationen Addition, Subtraktion und Skalarmultiplikation können neue Vektoren gebildet werden. Man spricht dabei von einer sog. Vektorkette bzw. Linearkombination.

Beispiel

Der Vektor $\vec c$ lässt sich als Vektorkette der Vektoren $\vec a$ und $\vec b$ darstellen:

\displaystyle \vec c=3\vec a-\vec b

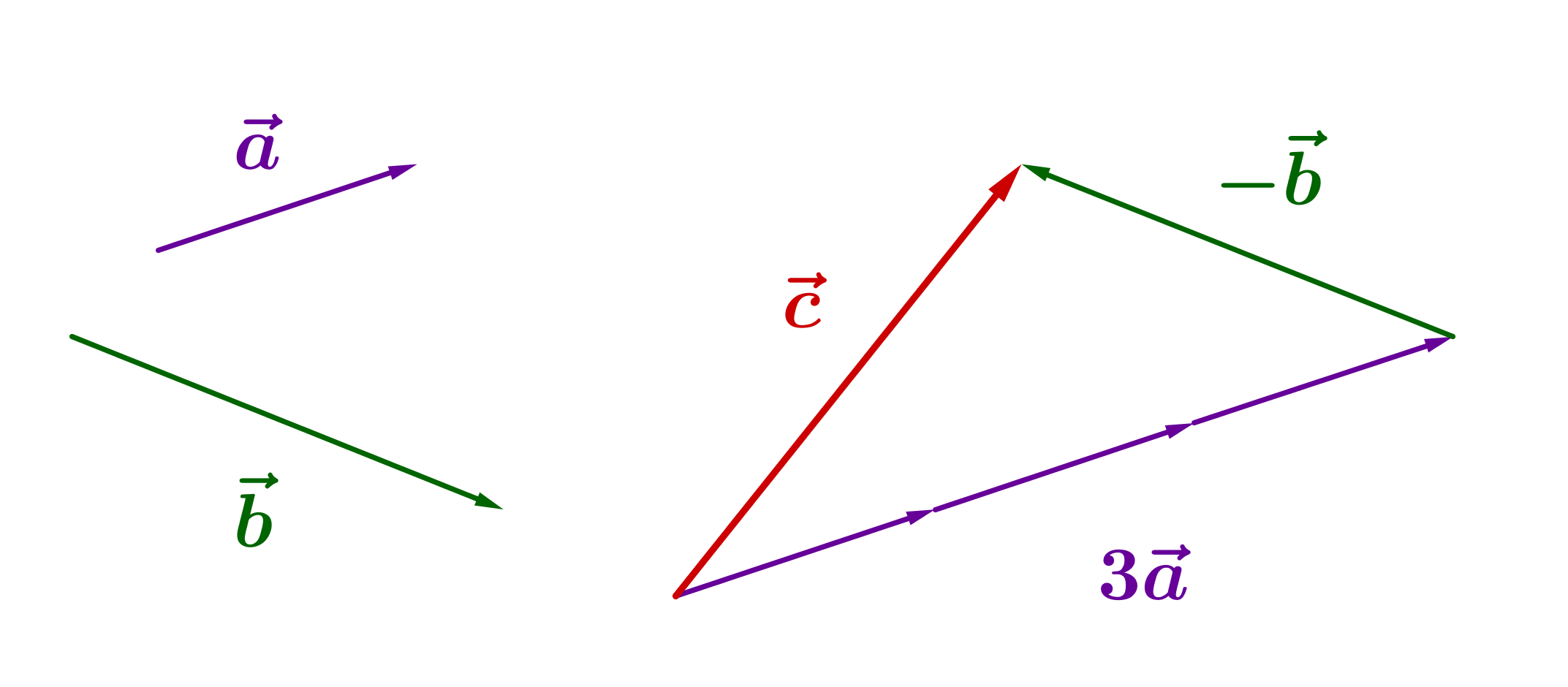
Ein Spezialfall davon ist die geschlossene Vektorkette, bei der die Spitze des letzten Vektors wieder auf den Fuß des ersten trifft; insgesamt ergibt sie somit $-$ egal, welche Vektoren darin vorkommen $-$ den Nullvektor.

Im obigen Beispiel können die drei Vektoren $\vec a$ , $\vec b$ und $\vec c$ folgendermaßen als geschlossene Vektorkette geschreiben werden:

\displaystyle 3\vec a-\vec b-\vec c=\vec 0

12 Aufgaben zur Vektorkette

Laden

13 Zusammenfassung

Mit Vektoren kann man (ähnlich wie mit normalen Zahlen) bestimmte Rechenoperationen durchführen:

Addition

Zwei Vektoren werden addiert, indem man ihre Koordinaten addiert:

\displaystyle \ \ \vec a + \vec b = \begin{pmatrix} x_a \\ y_a \end{pmatrix} + \begin{pmatrix} x_b \\ y_b \end{pmatrix} = \begin{pmatrix} x_a+x_b \\ y_a+y_b \end{pmatrix}

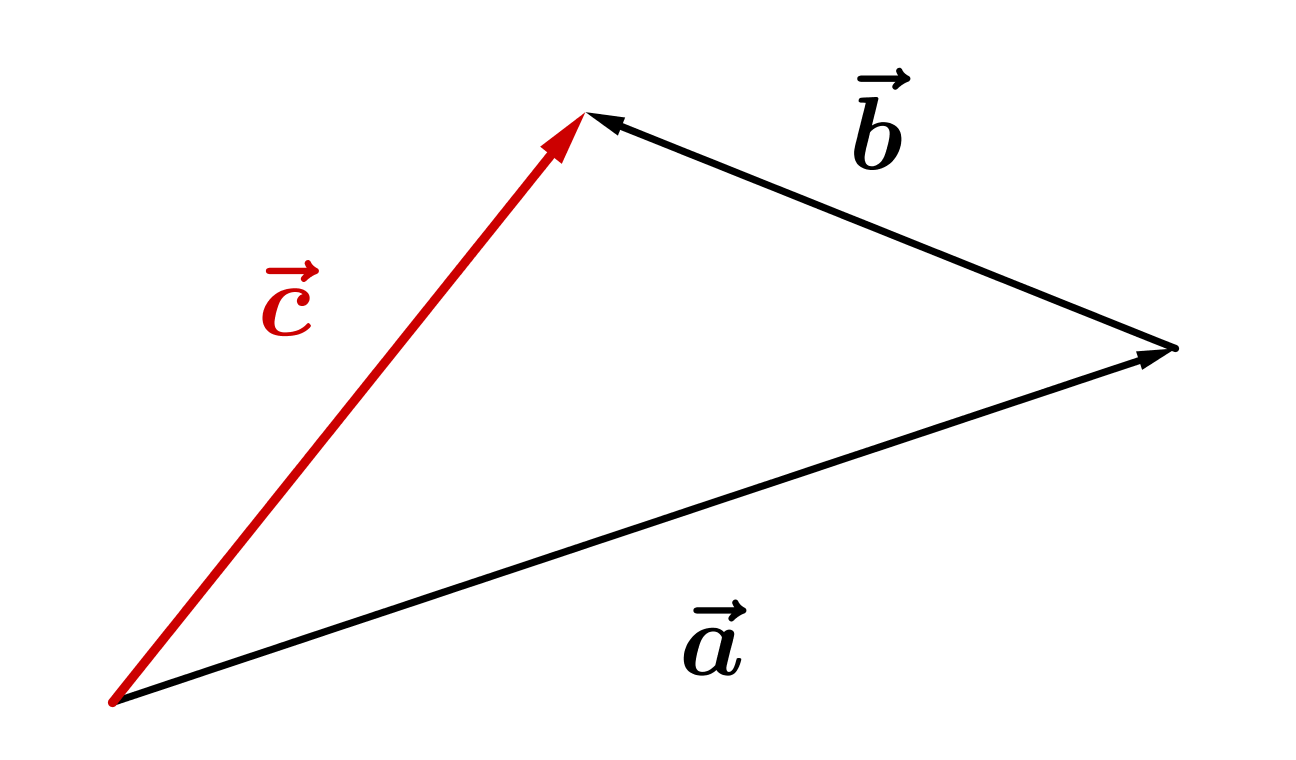
Subtraktion

Zwei Vektoren werden subtrahiert, indem man ihre Koordinaten subtrahiert:

\displaystyle \ \ \vec a - \vec b = \begin{pmatrix} x_a \\ y_a \end{pmatrix} - \begin{pmatrix} x_b \\ y_b \end{pmatrix} = \begin{pmatrix} x_a-x_b \\ y_a-y_b \end{pmatrix}

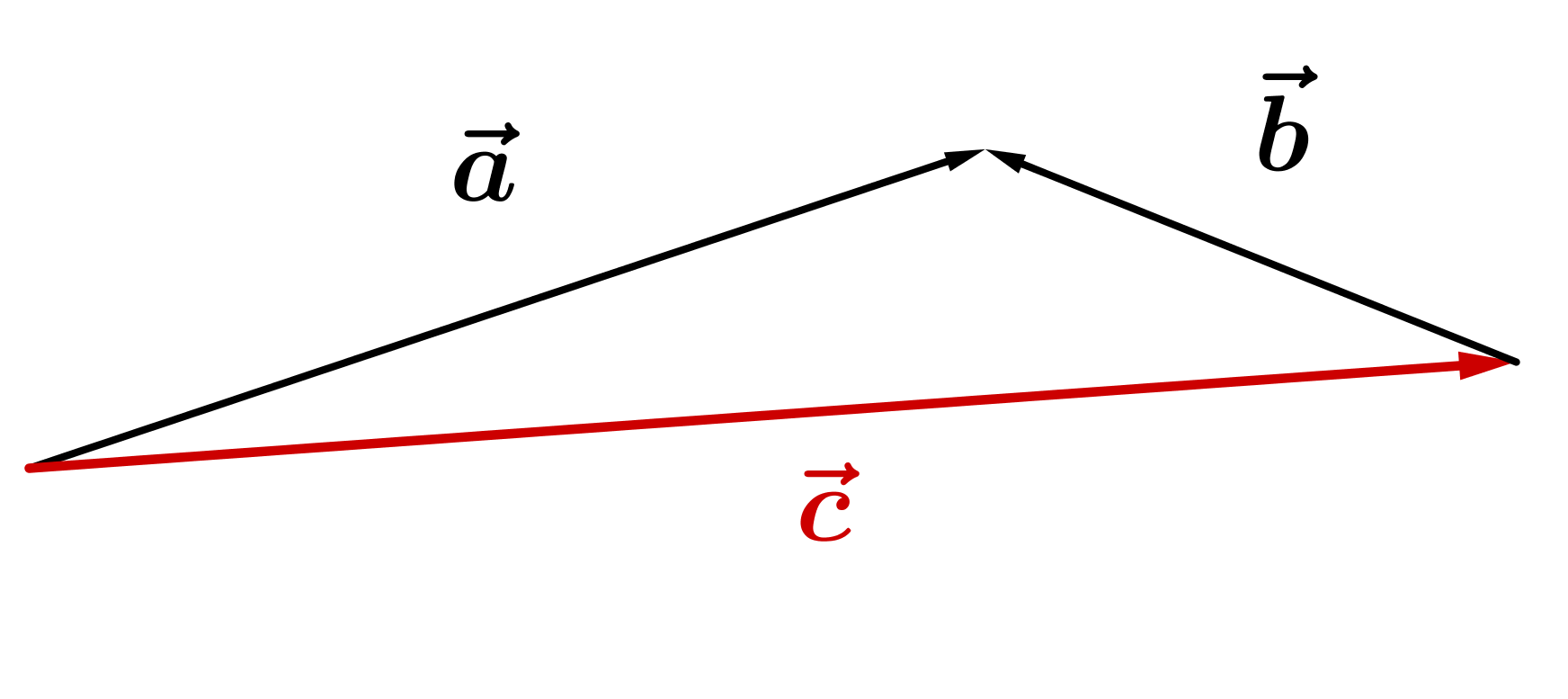
Skalarmultiplikation

Man multipliziert einen Vektor mit einer Zahl (="Skalar"), indem man seine Koordinaten mit der Zahl multipliziert:

\displaystyle \ \ k\cdot\vec a = k\cdot\begin{pmatrix} x_a \\ y_a \end{pmatrix} = \begin{pmatrix} k\cdot x_a \\ k\cdot y_a \end{pmatrix}

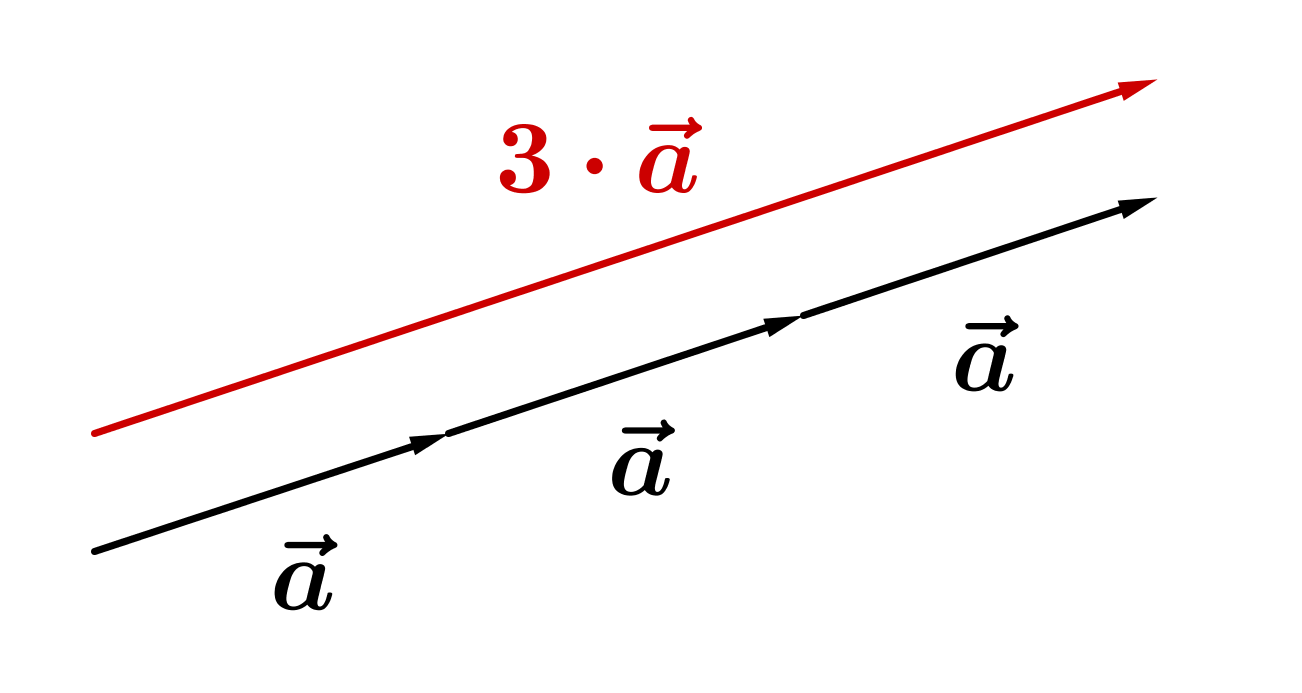
Vektorkette

Durch Kombination der obigen drei Operationen können neue Vektoren gebildet werden.

Bsp.: $\,\vec d = 3\vec a - 5\vec b + \frac{2}{7}\vec c$

14 Zeige, was du kannst!

Laden