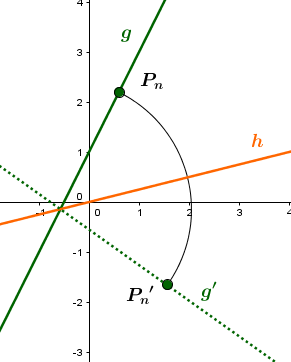
Spiegle die Gerade an der Ursprungsgeraden und gib die Gleichung der Bildgeraden an.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Spiegelung einer Geraden an einer Ursprungsgeraden
Somit ergibt sich folgende Gleichung:
Die gespiegelten Punkte haben also folgende Koordinaten:
Als letztes muss noch der Trägergraph bestimmt werden.
In Koordinatenform dargestellt ergibt sich:
Dazu löst man die Gleichung (1) nach auf.
Setze nun Gleichung in ein:
Die gespiegelte Gerade hat demnach folgende Gleichung:
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Spiegelung einer Geraden an einer Ursprungsgeraden
Somit ergibt sich folgende Gleichung:
Die gespiegelten Punkte haben also folgende Koordinaten:
Als letztes muss noch der Trägergraph bestimmt werden.
In Koordinatenform dargestellt ergibt sich:
Dazu löst man die Gleichung (1) nach auf.
Setze nun die Gleichung in ein:
Die gespiegelte Gerade hat demnach folgende Gleichung:
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Spiegelung einer Gerade an einer Ursprungsgerade
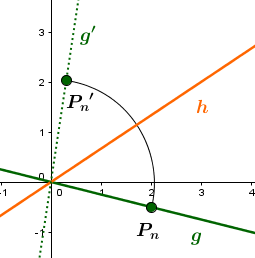
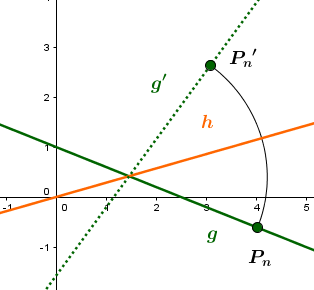
Die Gerade soll an der Geraden gespiegelt werden:
Das heißt, man wählt sich einen beliebigen Punkt auf der Geraden g und spiegelt diesen an der Geraden auf den Bildpunkt .
ist somit ein beliebiger Punkt auf der Bildgeraden .
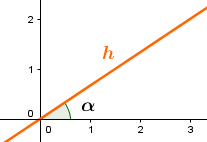
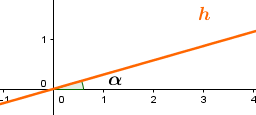
Um den Punkt an der Geraden zu spiegeln, benötigt man als erstes den Winkel , den die Gerade mit der x-Achse einschließt.
Somit ergibt sich folgende Gleichung:
Die gespiegelten Punkte haben also folgende Koordinaten:
Als letztes muss noch der Trägergraph bestimmt werden.
In Koordinatenform dargestellt ergibt sich:
Dazu löst man die Gleichung (1) nach auf.
Setze nun die Gleichung in ein:
Die gespiegelte Gerade hat demnach folgende Gleichung:
Hast du eine Frage oder Feedback?
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?