1 Übersicht
Inhalt des Kurses
In diesem Kurs wird die Abbildungsgleichung einer Spiegelung von Punkten und Geraden an einer Ursprungsgeraden hergeleitet und anhand von Beispielen erklärt.
Vorkenntnisse
Du solltest Vektoren im Zweidimensionalen verstanden haben.
Du solltest außerdem Vektoren zwischen zwei Punkten aufstellen und Vektoren addieren und subtrahieren können. Hier helfen dir auch diese beiden Kurse weiter: Vektoren in der Ebene I und Vektoren in der Ebene II.
Außerdem solltest du eine 2x2-Matrix mit einem Vektor multiplizieren können.
Kursdauer
1,5 Stunden
2 Motivation
Gegeben:
Ein Punkt und eine Gerade .
Aufgabenstellung:
Wie kann man den Bildpunkt einer Spiegelung von an berechnen? Gibt es eine allgemeine Formel für beliebige Punkte ?
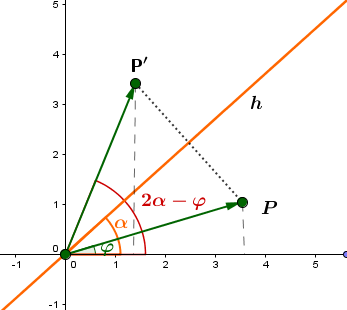
3 Herleitung der Abbildungsgleichung (1/2)
Der Punkt soll an der Ursprungsgeraden gespiegelt werden.
Auf den nächsten Kursseiten wird eine Abbildungsgleichung zum Berechnen des Bildpunktes hergeleitet:
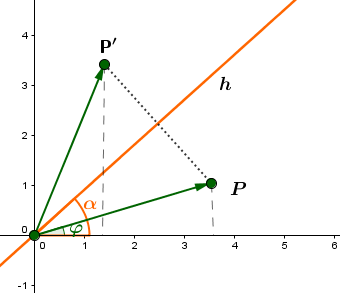
4 Herleitung der Abbildungsgleichung (2/2)
Zur Erinnerung:
Setzt man dies ein, erhält man:
Nun schreibt man das noch in der Matrixschreibweise, um sowohl den ursprünglichen Vektor als auch den Bildvektor hervorzuheben:
Im Spoiler findet man eine alternative Herleitung:
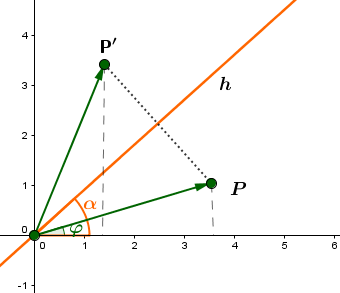
5 Abbildungsgleichung
Zusammenfassung
Hier noch einmal eine Zusammenfassung der hergeleiteten Abbildungsgleichung zum Spiegeln an einer Ursprungsgeraden.
In Koordinatenform:
In Matrixform:
Wobei hier der Schnittwinkel der Spiegelachse und der x-Achse ist. ist die Steigung von .
6 Beispiel: Punkt an Ursprungsgerade spiegeln
Beispiel
Spiegle den Punkt an der Ursprungsgeraden !
1. Berechnung von
Um den Punkt an der Geraden zu spiegeln, benötigt man als erstes den Winkel , den die Gerade mit der x-Achse einschließt.
2. Abbildungsgleichung aufstellen
Somit ergibt sich folgende Gleichung:
Der gespiegelte Punkt hat die Koordinaten .
7 Aufgaben: Spiegelung an einer Ursprungsgeraden
Jetzt bist du dran.
Laden
8 Spiegelung an besonderen Geraden
Da man sehr häufig an der x-Achse, y-Achse und an der Winkelhalbierenden spiegelt, bietet es sich an, dass man sich für diese besonderen Spiegelungen eine Übersicht erstellt:
Achsenspiegelung an der x-Achse
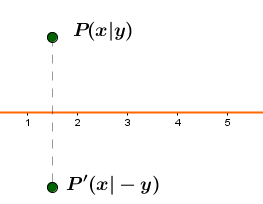
Achsenspiegelung an der y-Achse
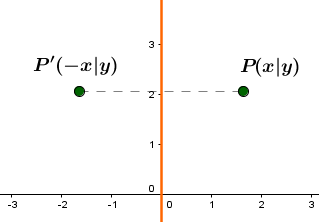
Achsenspiegelung an der Winkelhalbierenden des I. und III. Quadranten
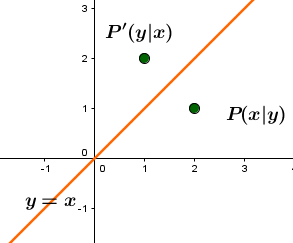
Achsenspiegelung an der Winkelhalbierenden des II. und IV. Quadranten
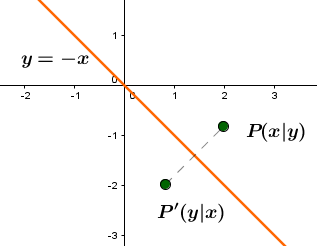
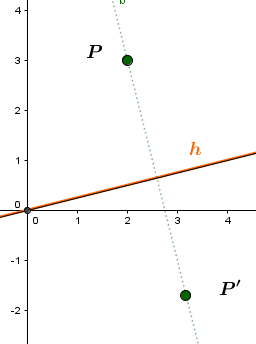
9 Beispiel: Gerade an Ursprungsgeraden spiegeln
Die Gerade soll an der Geraden gespiegelt werden.
Man wählt also einen beliebigen Punkt auf der Geraden und bildet diesen durch Achsenspiegelung an der Geraden auf den Bildpunkt ab.
ist somit ein beliebiger Punkt auf der Bildgeraden .
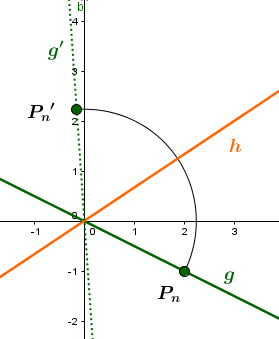
1. Berechnung von
Um den Punkt an der Geraden zu spiegeln, benötigt man als erstes den Winkel , den die Gerade mit der -Achse einschließt.
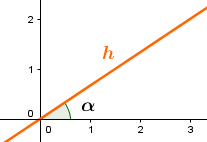
2. Abbildungsgleichung aufstellen
Somit ergibt sich folgende Gleichung:
Die gespiegelten Punkte haben also die Koordinaten .
3. Trägergraph bestimmen
Als letztes muss noch der Trägergraph der Punkte bestimmt werden.
Für die Punkte gilt ja:
Nun löst man die Gleichung nach auf und setzt dann in ein:
Die gespiegelte Gerade besitzt also folgende Gleichung:
10 Aufgaben: Gerade an Ursprungsgeraden spiegeln
Jetzt bist du dran.
Laden
11 Beispiel: Spiegelachse berechnen
Der Bildpunkt entsteht durch Spiegelung des Urpunktes an einer Ursprungsgeraden .
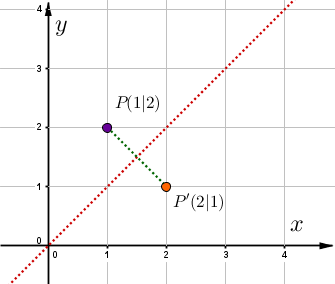
Man benutzt die Abbildungsgleichung und setzt die Punkte und ein, dann löst man nach auf.
Nun setzt man in ein und löst nach auf.
Man hat also den Winkel bestimmt, unter dem sich die Spiegelachse mit der x-Achse schneidet.
Damit kann man auf die Steigung der Geraden schließen und somit die Geradengleichung für aufstellen.
12 Zusammenfassung und Ausblicke
Hier noch einmal eine Zusammenfassung des in diesem Kurs behandelten Stoffes:
Spiegelung an einer Ursprunsgeraden
in Koordinatenform:
in Matrixform:
Zugehörige Themen
Kurs: Drehung
Artikel: Verknüpfung von Abbildungen
weitere Aufgaben und Artikel zum Thema: Abbildungen im Koordinatensystem