Gemischte Aufgaben zu quadratischen Funktionen

…

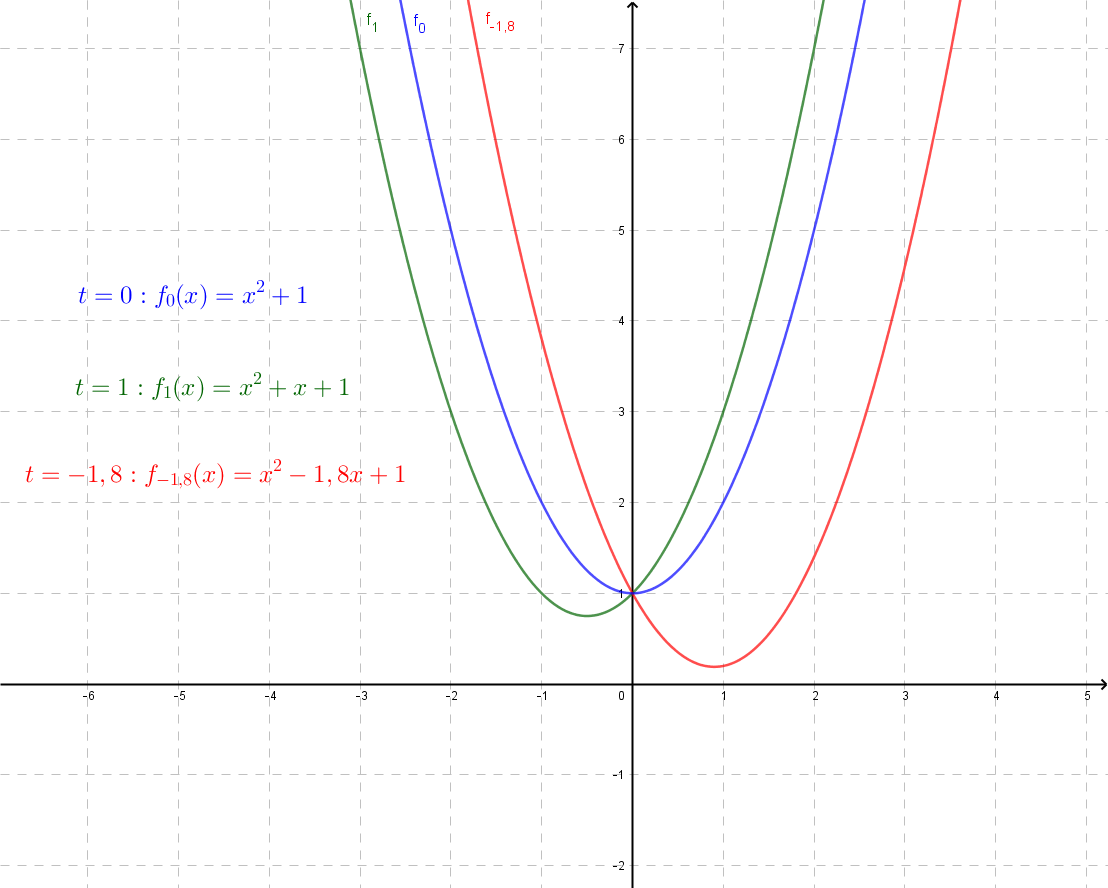
Welche Werte kann der Parameter t annehmen, so dass die folgenden Aussagen richtig sind?

Der Graph der Funktion f mit $f\left(x\right)=x^2+tx+1$ verläuft vollständig oberhalb der x-Achse.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Quadratische Funktionen

Eine quadratische Funktion ist eine ganzrationale Funktion zweiten Grades.

Es werden zwei mögliche Lösungswege vorgestellt.

1.Lösungsweg: Betrachtung der Diskriminanten

\displaystyle x^2+tx+1=0

Diskriminante: $D = t^{2} - 4$ .

Als Bedingung dafür, dass keine Nullstelle existiert, ergibt sich nun $D = t^{2} - 4 < 0$ .

\displaystyle t^2-4<0\;\Leftrightarrow\;t\in\;]{-2};2[

Daher liegt $t$ im Intervall $] - 2; 2 [$ .

2.Lösungsweg: Scheitelpunkt ermitteln

Gegeben ist die Funktion:

$f(x)=x^2+tx+1;\;x\in R$

Der Graph der Funktion $f (x)$ soll oberhalb der $x$ - Achse verlaufen.

Daraus folgt für alle Werte $f (x) > 0$ .

Der Scheitelpunkt der Parabel muss also auch oberhalb der $x$ -Achse liegen.

$\displaystyle f\left(x\right)$	$=$	$\displaystyle x^2+tx+1$
	↓	Quadratische Ergänzung
	$=$	$\displaystyle x^2+tx+(\frac{t}{2})^2-(\frac{t}{2})^2+1$
	↓	Binom bilden
	$=$	$\displaystyle (x+\frac{t}{2})^2+1-(\frac{t}{2})^2$
	↓	Scheitelpunktsform bestimmen
	$=$	$\displaystyle (x+\frac{t}{2})^2+1-\frac{t^2}{4}$

Der Scheitelpunkt ist also $S(\;-\frac t{2\;}|1-\frac{t^2}4)$ .

Die $y$ -Koordinate des Scheitels muss oberhalb der $x$ -Achse liegen also $f (t) > 0$ . Daraus folgt die Ungleichung:

$1 - 4 t^{2} > 0 \Leftrightarrow t^{2} < 4 1−4t^2>0⇔t^2<4$

Lösen der Ungleichung:

Wurzel ziehen und beachten, dass sowohl negative als auch

positive Werte auftreten können.

Ergebnis:

Der Paramter $t$ liegt im Intervall $] - 2; 2 [$ .

Hast du eine Frage oder Feedback?

Kommentiere hier 👇

Der Scheitel des Graphen der Funktion f mit $f\left(x\right)=-x^2-tx-2$ liegt auf der x-Achse.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Quadratische Funktionen

Eine quadratische Funktion ist eine ganzrationale Funktion zweiten Grades.

$f (x) = - x^{2} - t x - 2$

1.Lösungsmöglichkeit: Diskriminante

Da der Scheitel der zugehörigen Parabel auf der x-Achse liegen soll, hat die quadratische Gleichung $- x^{2} - t x - 2 = 0$ genau eine Lösung. Für die Diskriminante muss also $D = 0$ gelten.

$D=t^2-4\cdot(-2)\cdot(-1)=t^2-8=0$

Also ist $t=\sqrt8$ oder $t=-\sqrt8$ .

2.Lösungsmöglichkeit: Scheitelform

Mit der Scheitelform einer quadratischen Funktion kann der Scheitelpunkt abgelesen werden.

$\displaystyle f(x)$	$=$	$\displaystyle -x^2-tx-2$
	$=$	$\displaystyle -[x^2+tx+\frac{t^2}{4}-\frac{t^2}{4}]-2$
	$=$	$\displaystyle -[(x+\frac{t}{2})^2-\frac{t^2}{4}]-2$
	$=$	$\displaystyle (x+\frac{t}{2})^2+\frac{t^2}{4}-2$

Der Scheitel der zugehörigen Parabel liegt also bei $(-\frac t2\vert\frac{t^2}4-2)$ .

Da der Scheitel auf der x-Achse liegen soll und dessen y-Koordinate damit $0$ ist, muss $\frac{t^2}4-2=0$ gelten.

Also: $t^{2} = 8$ und damit $t=\sqrt8$ oder $t=-\sqrt8$ .

Hast du eine Frage oder Feedback?

Kommentiere hier 👇

Der Scheitel des Graphen der Funktion f mit $f\left(x\right)=-x^2-tx-2$ liegt auf der y-Achse.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Quadratische Funktionen

Eine quadratische Funktion ist eine ganzrationale Funktion zweiten Grades.

$f\left(x\right)=-x^2-tx-2$

1.Lösungsweg: Achsensymmetrie

Da der Scheitel der Parabel auf der y-Achse liegen soll, muss $f (x) = f (- x)$ für alle $x\in\mathbb{R}$ gelten.

Damit gilt: $- (x)^{2} - t x - 2 = - (- x)^{2} - t (- x) - 2$

Also: $- t x = t x$ $\Rightarrow2tx=0$ $\Rightarrow t=0$ .

2.Lösungsweg: Scheitelform

Mit der Scheitelform einer quadratischen Funktion kann der Scheitelpunkt abgelesen werden.

$\displaystyle f\left(x\right)$	$=$	$\displaystyle -x^2-tx-2$
	↓	Ergänze quadratisch
	$=$	$\displaystyle -[x^2+tx+\frac{t^2}{4}-\frac{t^2}{4}]-2$
	↓	Binomische Formel
	$=$	$\displaystyle -[(x+\frac{t}{2})^2-\frac{t^2}{4}]-2$
	↓	Klammern auflösen
	$=$	$\displaystyle -(x+\frac{t}{2})^2+\frac{t^2}{4}-2$

Der Scheitel der zugehörigen Parabel liegt also bei $(-\frac t2\vert\frac{t^2}4-2)$ .

Da der Scheitel auf der y-Achse liegen soll und dessen x-Koordinate dafür $0$ sein muss, muss $-\frac t2=0$ gelten, also $t = 0$ .

Hast du eine Frage oder Feedback?

Kommentiere hier 👇

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0

serlo.org CC BY-SA 4.0

→ Was bedeutet das?