Besondere Eigenschaften reellwertiger Funktionen

Hier findest du eine Liste von Eigenschaften, die manche Funktionen erfüllen können. In der Schule interessiert man sich meistens für Funktionen, die eine reelle Zahl auf eine weitere reelle Zahl abbilden, sogenannte reellwertige Funktionen. Im Folgenden wird $f$ immer so eine Funktion sein.

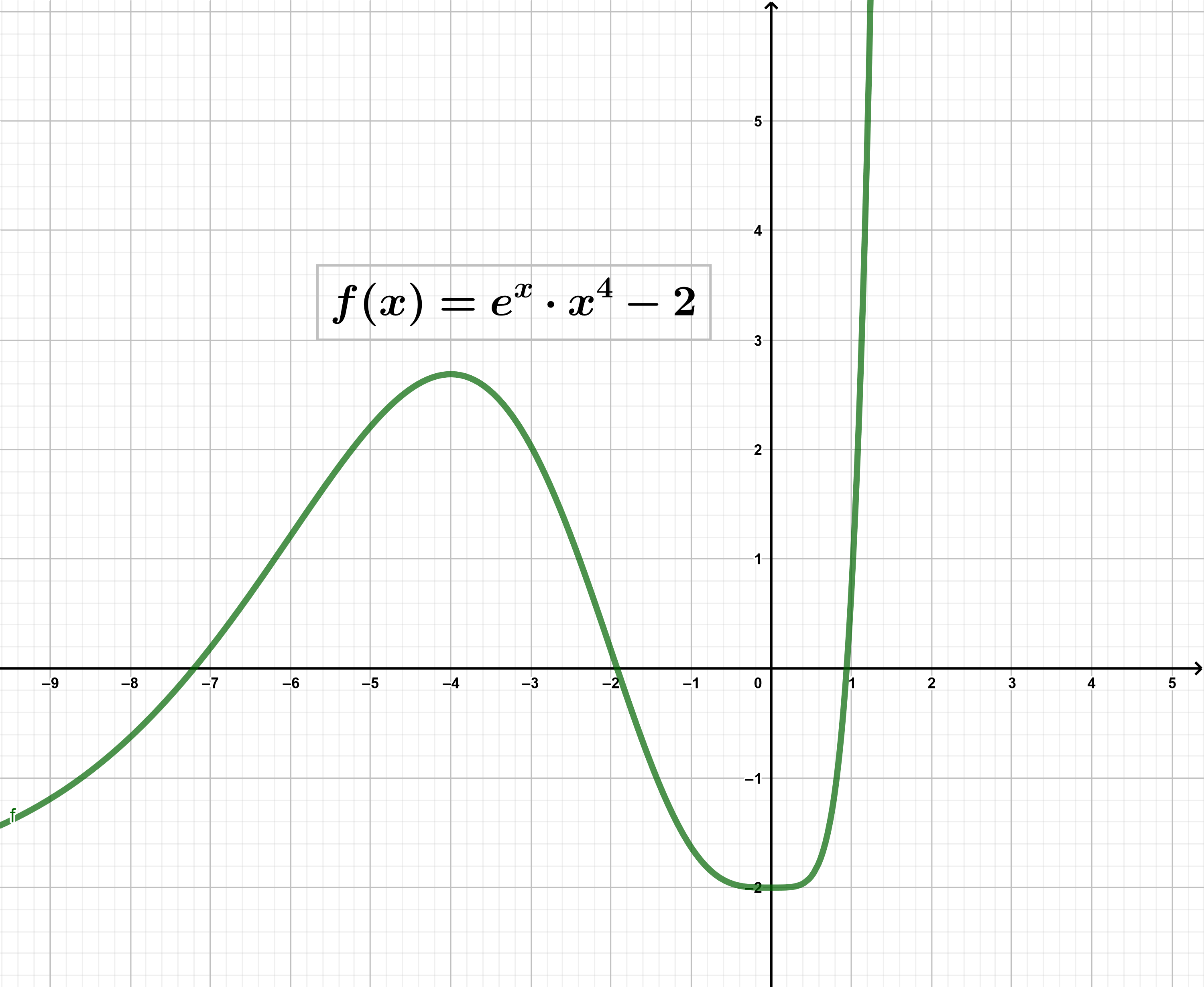
Monotonie

Eine Funktion ist monoton bzw. auf einem Abschnitt monoton, wenn…

Beschreibung in Formeln	Kurze Erklärung am Graphen
für alle Stellen $x < y$ in diesem Abschnitt $f (x) \leq f (y)$ gilt oder für alle $x < y$ , $f (x) \geq f (y)$ gilt	der Graph von $f$ entweder von links unten nach rechts oben, oder von links oben nach rechts unten verläuft. Diese "Laufrichtung" muss der Graph immer erhalten.

Beispiel 1

f (x) = \frac{1}{3} x + 2

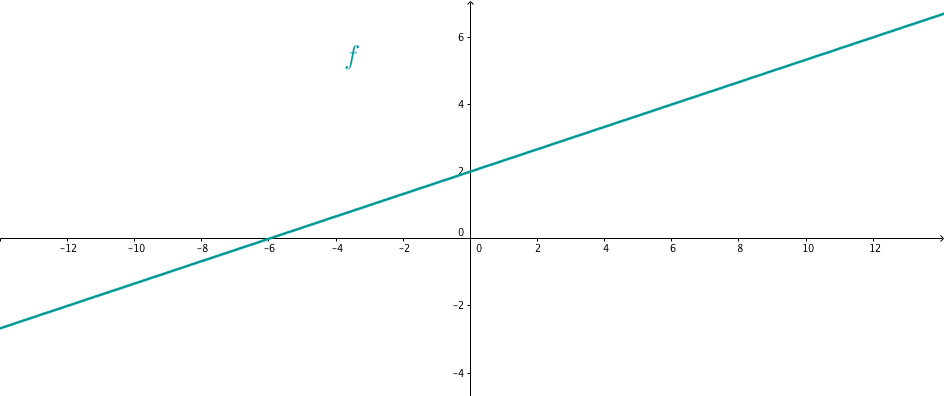
$f$ ist in diesem Fall eine monoton steigende Funktion.

Beispiel 2

Die Funktion $f (x) = \frac{1}{2} [s i n (x) - x]$ , ist monoton fallend. Probiere doch an folgendem Applet aus, um rauszufinden warum das so ist.

Mit einem Klick auf Bild oder Button oben stimmst du zu, dass externe Inhalte von GeoGebra geladen werden. Dabei können persönliche Daten zu diesem Service übertragen werden – entsprechend unserer Datenschutzerklärung.

[https://www.geogebra.org/material/iframe/id/Tptjagc3]

Symmetrie

wenn…

Beschreibung in Formeln	Kurze Erklärung am Graphen
für alle $x$ gilt $f (x) = f (- x)$ oder für alle $x$ gilt $f (x) = - f (- x)$	Der Graph von $f$ ist symmetrisch zur y-Achse oder der Graph von f ist punktsymmetrisch zum Ursprung

Beispiel 3

f (x) = \frac{1}{3} x^{2} - 4

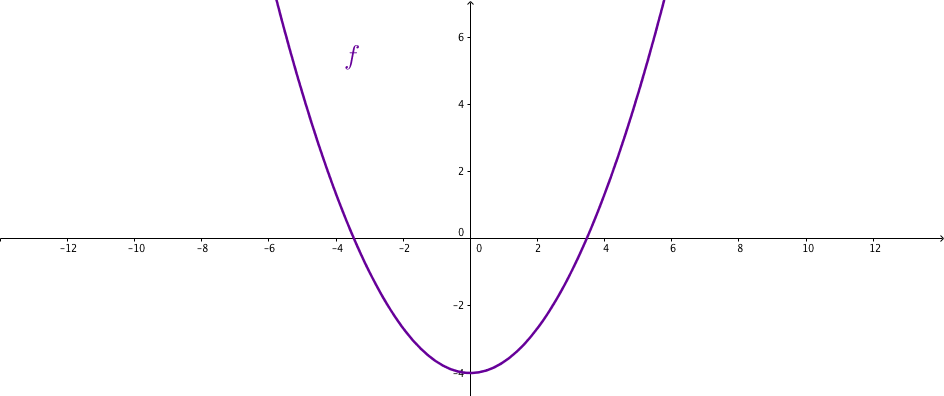
Diese Funktion ist achsensymmetrisch.

Beispiel 4

f (x) = \frac{1}{4} x^{3} - 9 x

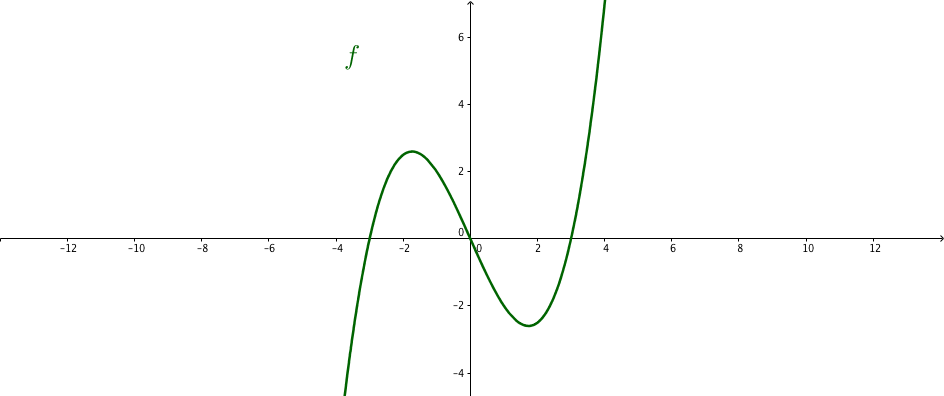
Diese Funktion ist punktsymmetrisch zum Ursprung.

Stetigkeit

Eine Funktion $f$ heißt stetig wenn…

Beschreibung in Formeln	Kurze Erklärung am Graphen
$\lim_{x \to x_{0}^{+}} f (x) = \lim_{x \to x_{0}^{-}} f (x)$ an jeder Stelle $x_{0}$ .	der Graph von $f$ an keiner Stelle Sprünge macht, oder unkontrolliert oszilliert.

Der Graph der Funktion $f (x) = e^{x} \cdot x^{4} - 2$ verläuft wie eine durchgezogene Linie, ohne Unterbrechung. Diesen Graphen würde man als stetig bezeichnen.

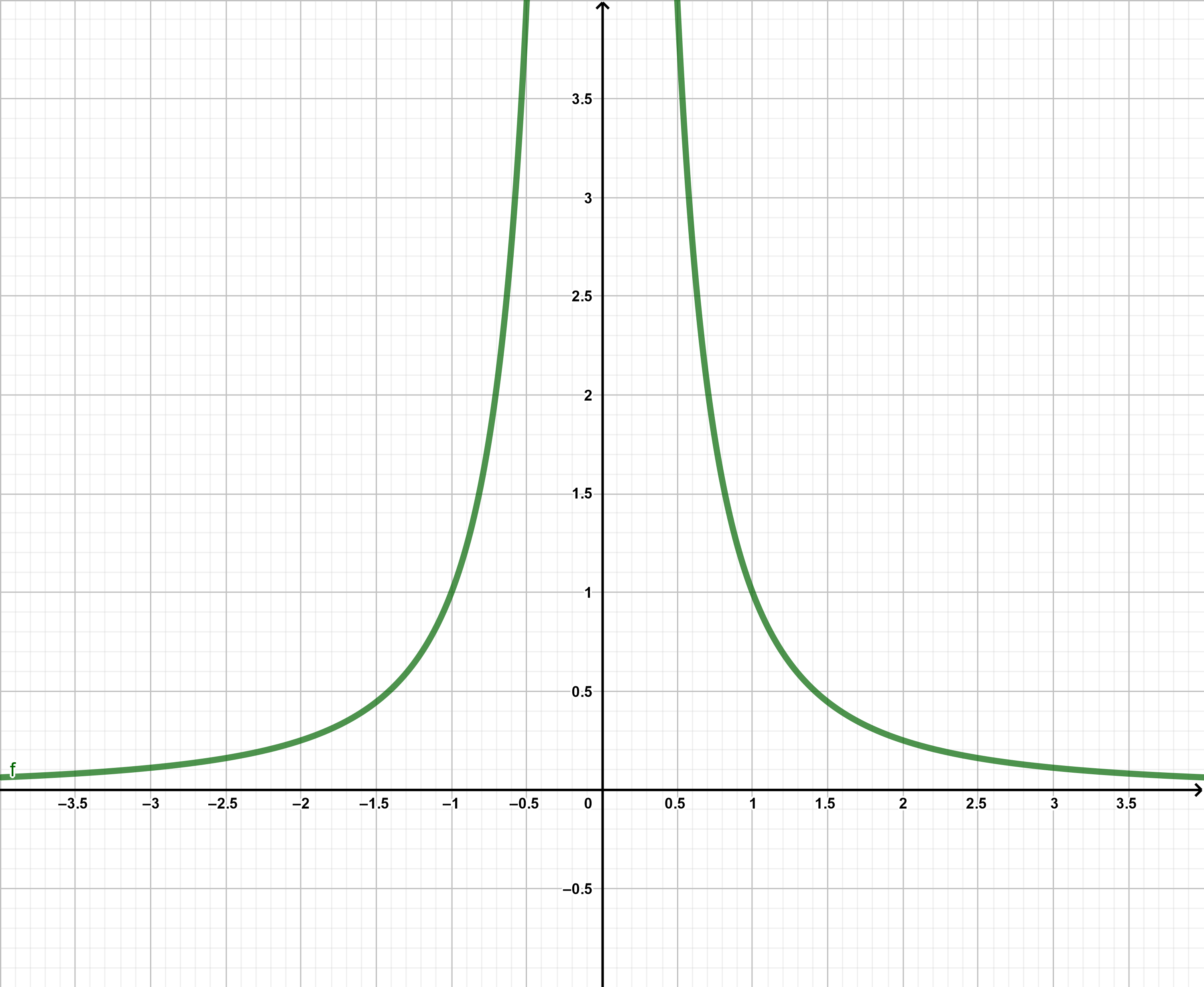
Die Funktion $f (x) = \frac{1}{x^{2}}$ besitzt eine Definitionslücke an der Stelle $x_{0} = 0$ . Infolgedessen macht der Graph der Funktion einen Sprung - er ist unstetig.

Du hast noch nicht genug vom Thema?

Hier findest du noch weitere passende Inhalte zum Thema:

Artikel

Übersicht über wichtige Funktionstypen

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

Besondere Eigenschaften reellwertiger Funktionen

Monotonie

Beschreibung in Formeln

Kurze Erklärung am Graphen

Beispiel 1

Beispiel 2

Symmetrie

Beschreibung in Formeln

Kurze Erklärung am Graphen

Beispiel 3

Beispiel 4

Stetigkeit

Beschreibung in Formeln

Kurze Erklärung am Graphen

Du hast noch nicht genug vom Thema?

Artikel