In diesem Artikel sind wichtige Typen von Funktionen zusammengestellt, die häufig verwendet werden.
Genaueres zu den einzelnen Funktionstypen findet man jeweils in den zugehörigen Serlo-Artikeln.
Polynome und Potenzen mit natürlichen Exponenten
Lineare Funktionen
Der Funktionsterm einer linearen Funktion hat die Form
Der Graph einer linearen Funktion ist stets eine Gerade.
Merkspruch: Den Graphen einer linearen Funktion kann man mit dem Lineal zeichnen.

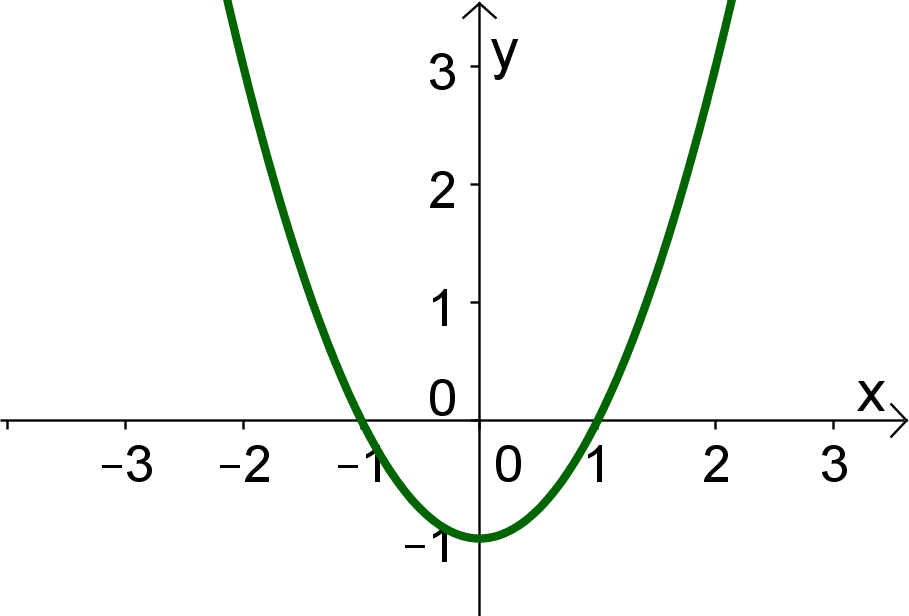
Quadratische Funktionen
Der Funktionsterm einer quadratischen Funktion hat die Form
(oder lässt sich in diese Form bringen).
Der Graph einer quadratischen Funktion ist stets eine Parabel.
Parabeln haben ein typisches bogenförmiges Aussehen und können nach oben oder nach unten geöffnet sein.
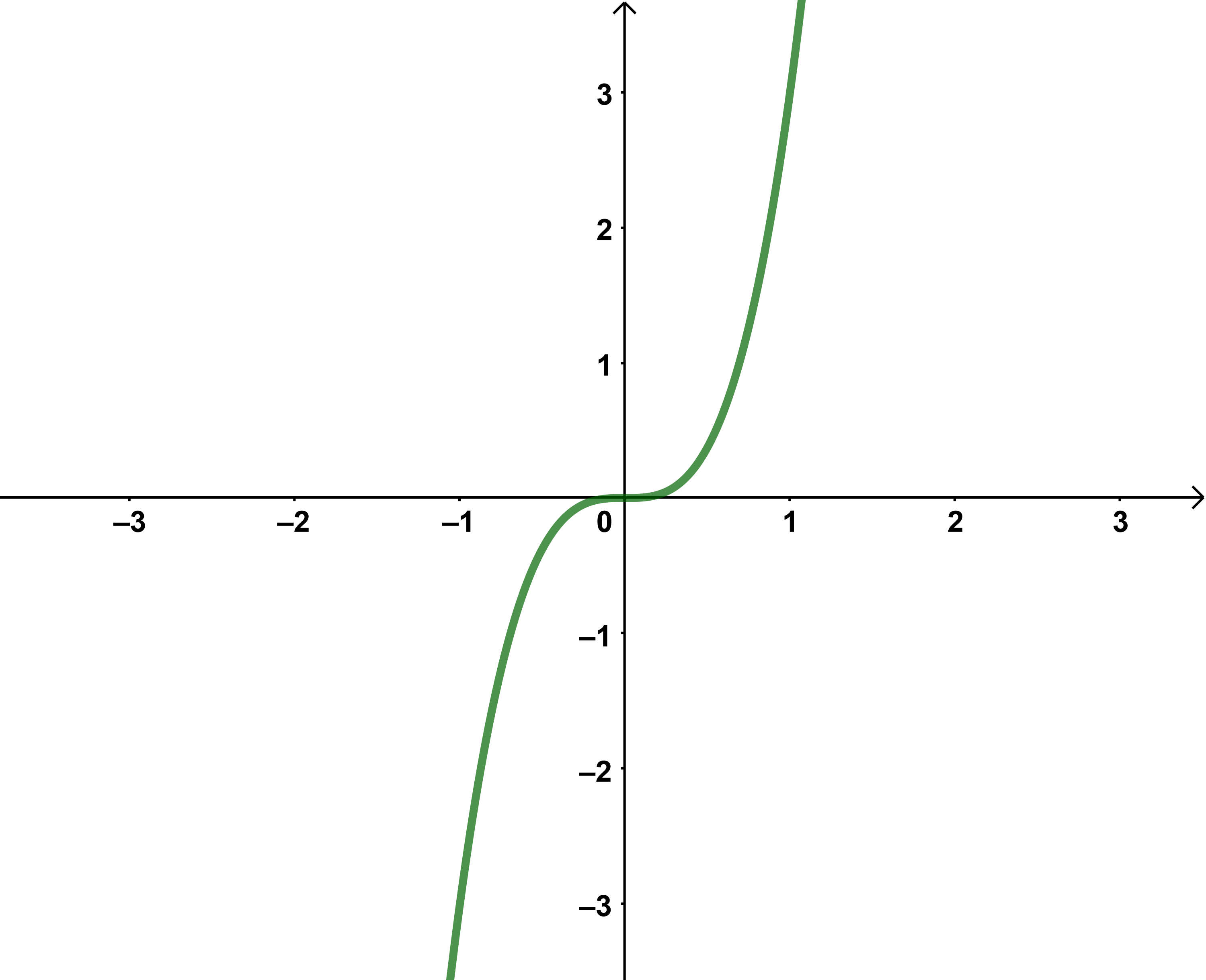
Potenzfunktionen mit natürlichen Exponenten
Der Funktionsterm einer Potenzfunktion lässt sich schreiben in der Form
Der Graph einer Potenzfunktion hat einen charakteristischen Verlauf, der davon abhängig ist,
ob gerade oder ungerade ist,
und welches Vorzeichen hat.
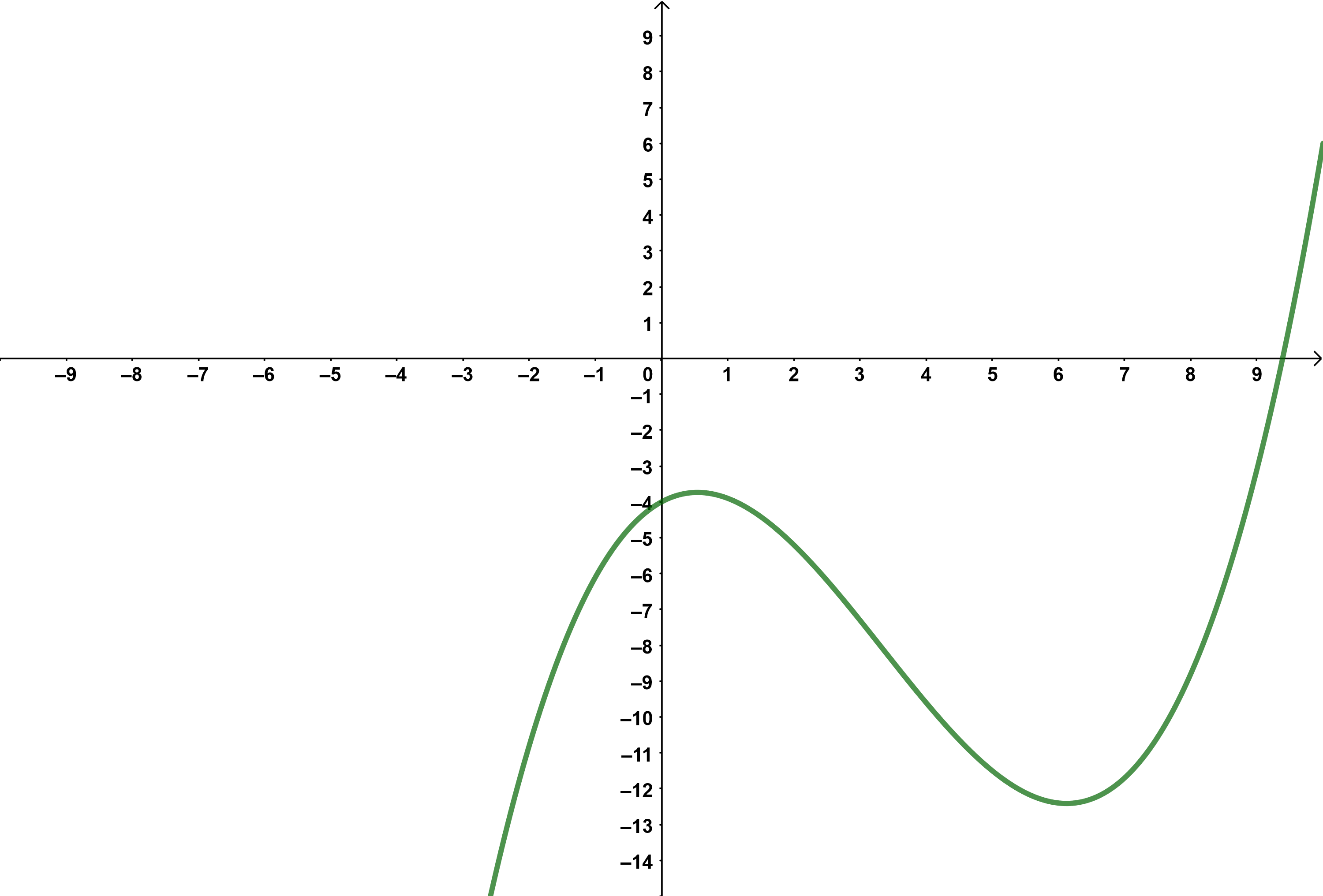
Polynomfunktionen (= ganzrationale Funktionen)
Der Funktionsterm einer Polynomfunktion lässt sich schreiben in der Form
Der Graph einer Polynomfunktion wird im Unendlichen vor allem durch den Term mit der höchsten x-Potenz bestimmt. Der charakteristische Verlauf des Graphen ist abhängig davon, ob gerade oder ungerade ist, und welches Vorzeichen hat.
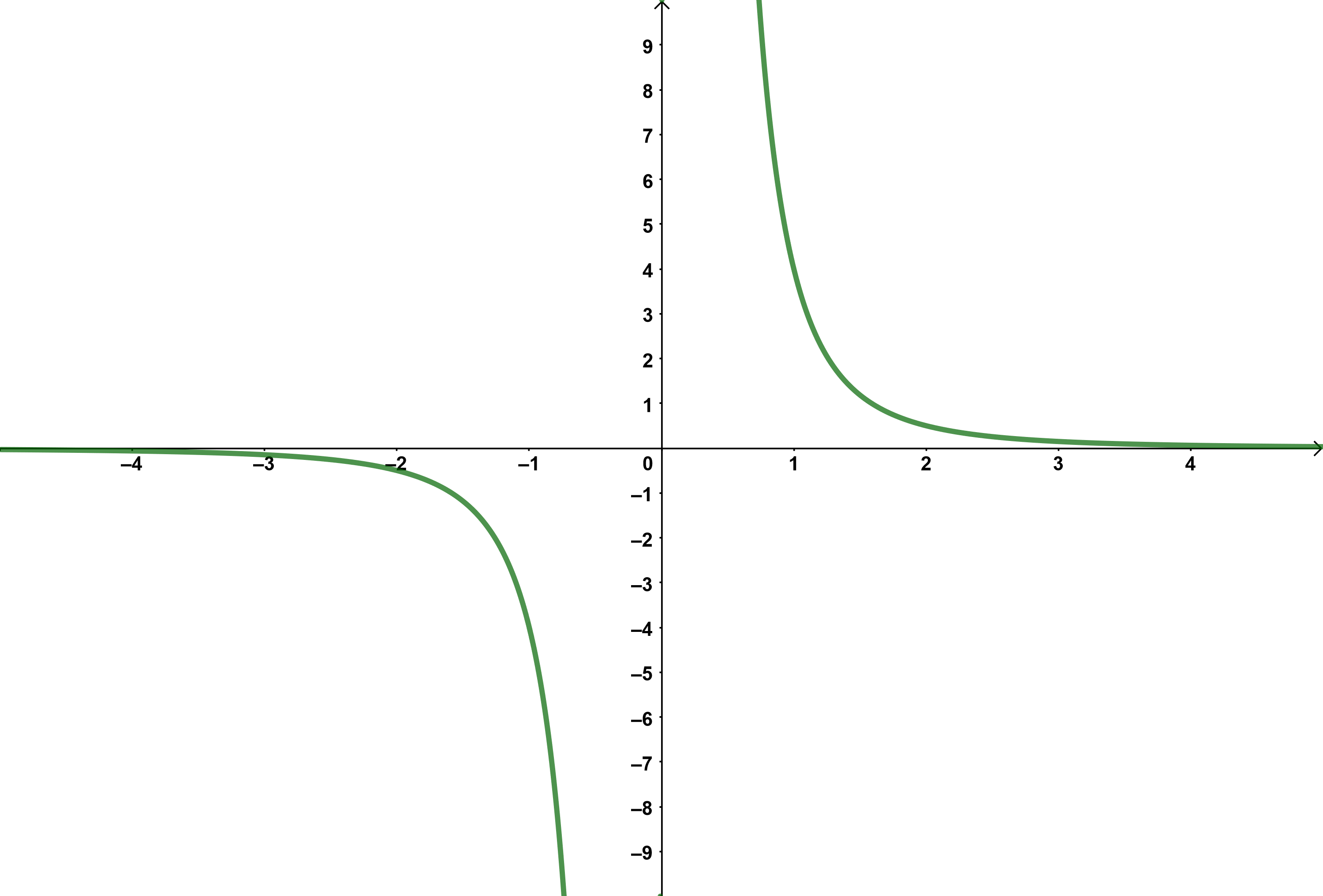
Potenzen mit negativen und gebrochenen Exponenten
Gebrochen-rationale Funktionen
Der Funktionsterm einer gebrochen-rationalen Funktion lässt sich schreiben in der Form
wobei und Polynomfunktionen sind und mindestens Grad 1 hat.
An den Stellen, an denen das Nennerpolynom den Wert annehmen würde, hat eine gebrochen-rationale Funktion Definitionslücken.
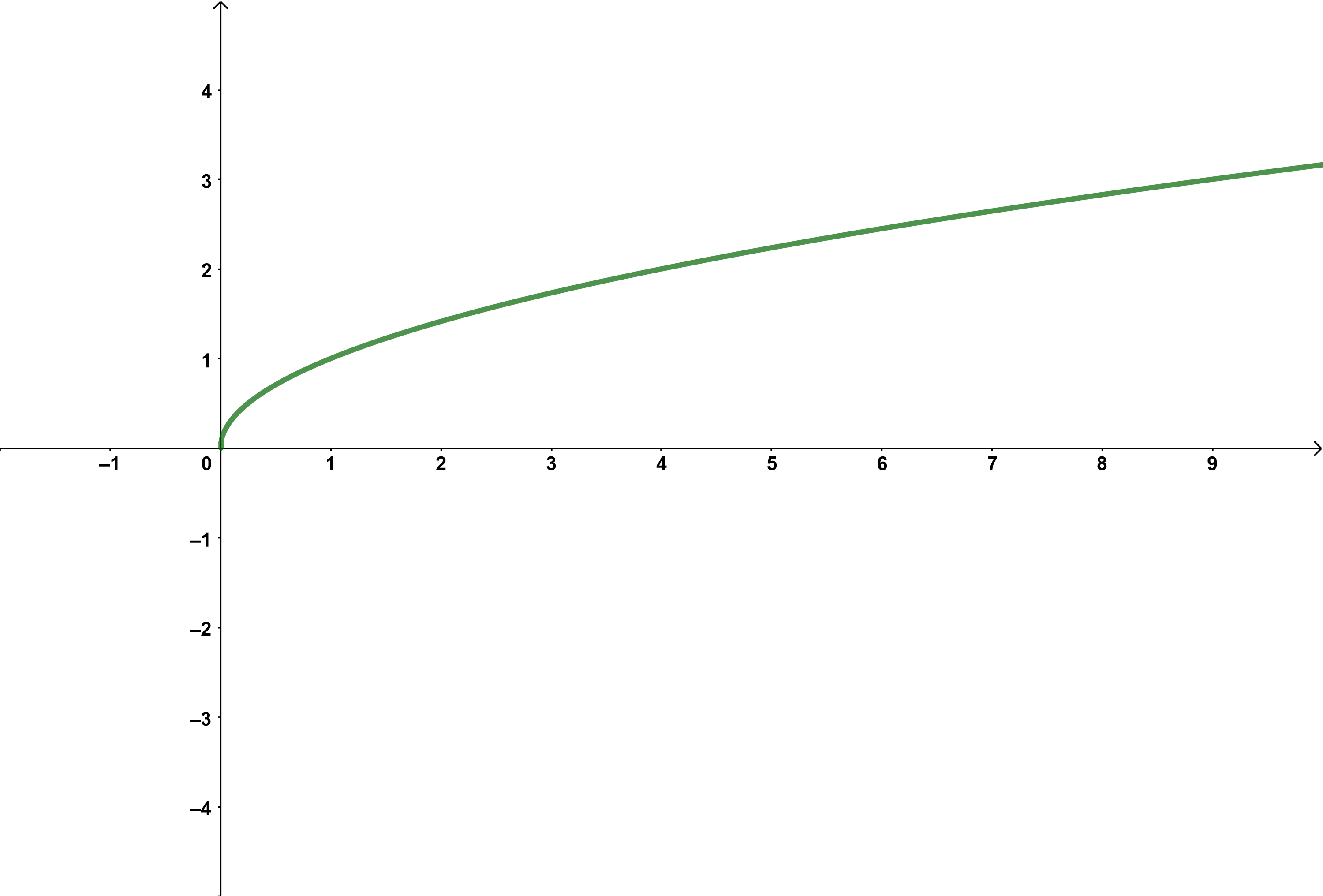
Wurzelfunktionen
Der Term der Wurzelfunktion ist von der Form
Exponential- und Logarithmusfunktionen
Exponentialfunktionen
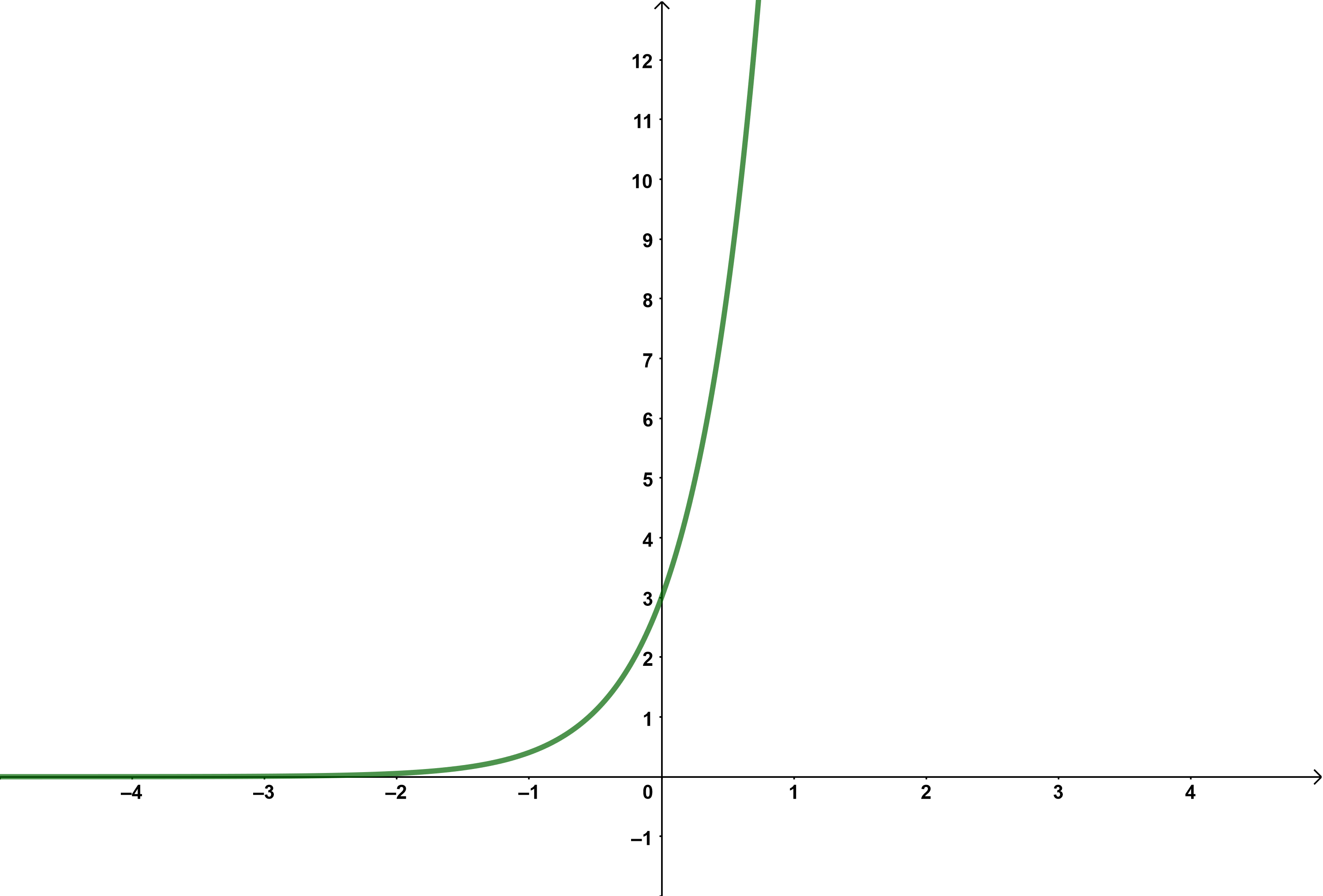
Der Funktionsterm einer Exponentialfunktion lässt sich schreiben in der Form: Dabei muss und sein.
Der Graph einer Exponentialfunktion
verläuft stets oberhalb der -Achse
ist streng monoton
nähert sich an der einen Seite an die x-Achse an, und geht an der anderen Seite gegen .
Logarithmusfunktionen
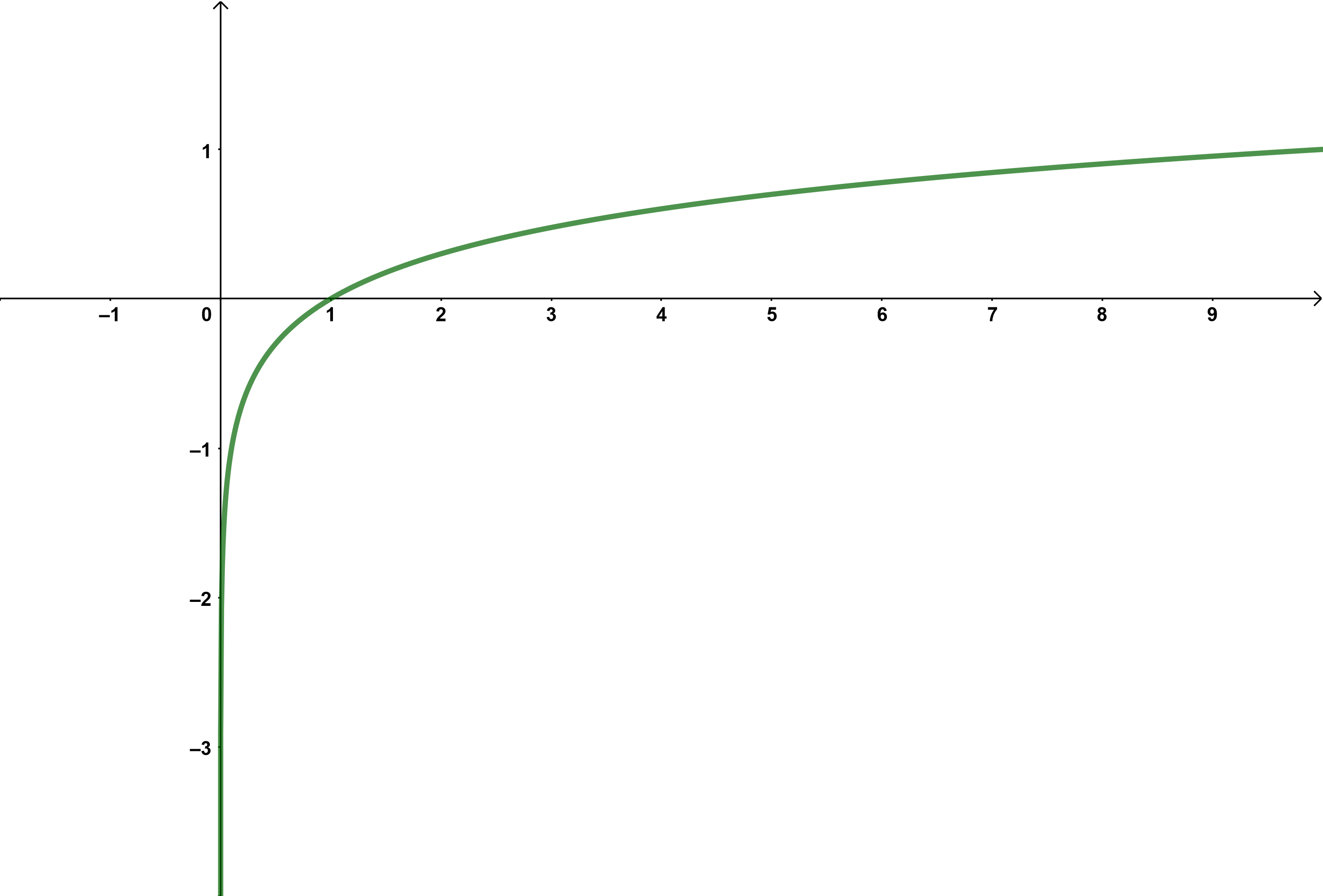
Der Funktionsterm lautet in seiner einfachsten Form
und bezeichnet den "Logarithmus zur Basis ".
Ein besonderer Logarithmus ist der "Logarithmus naturalis"
Trigonometrische Funktionen
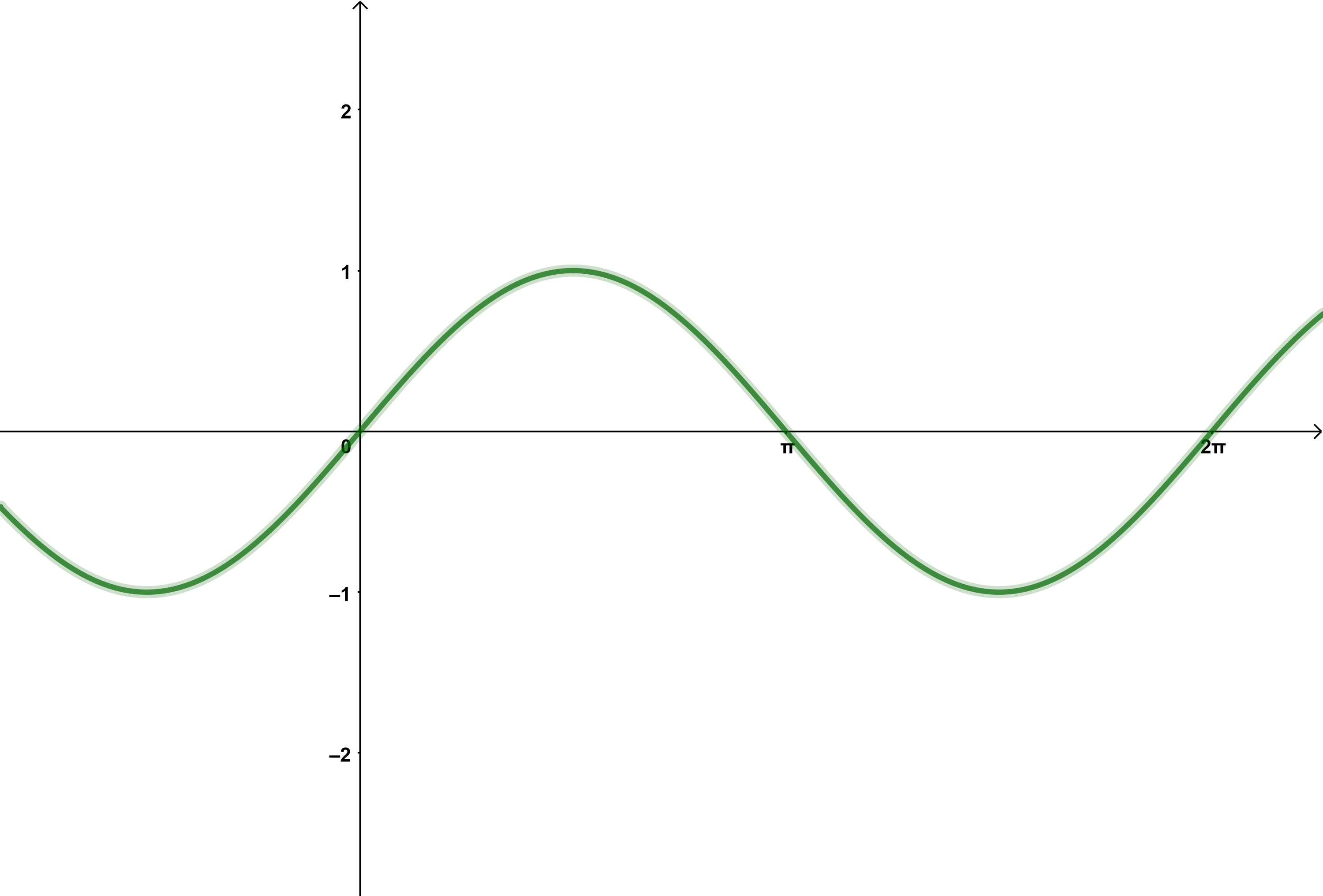
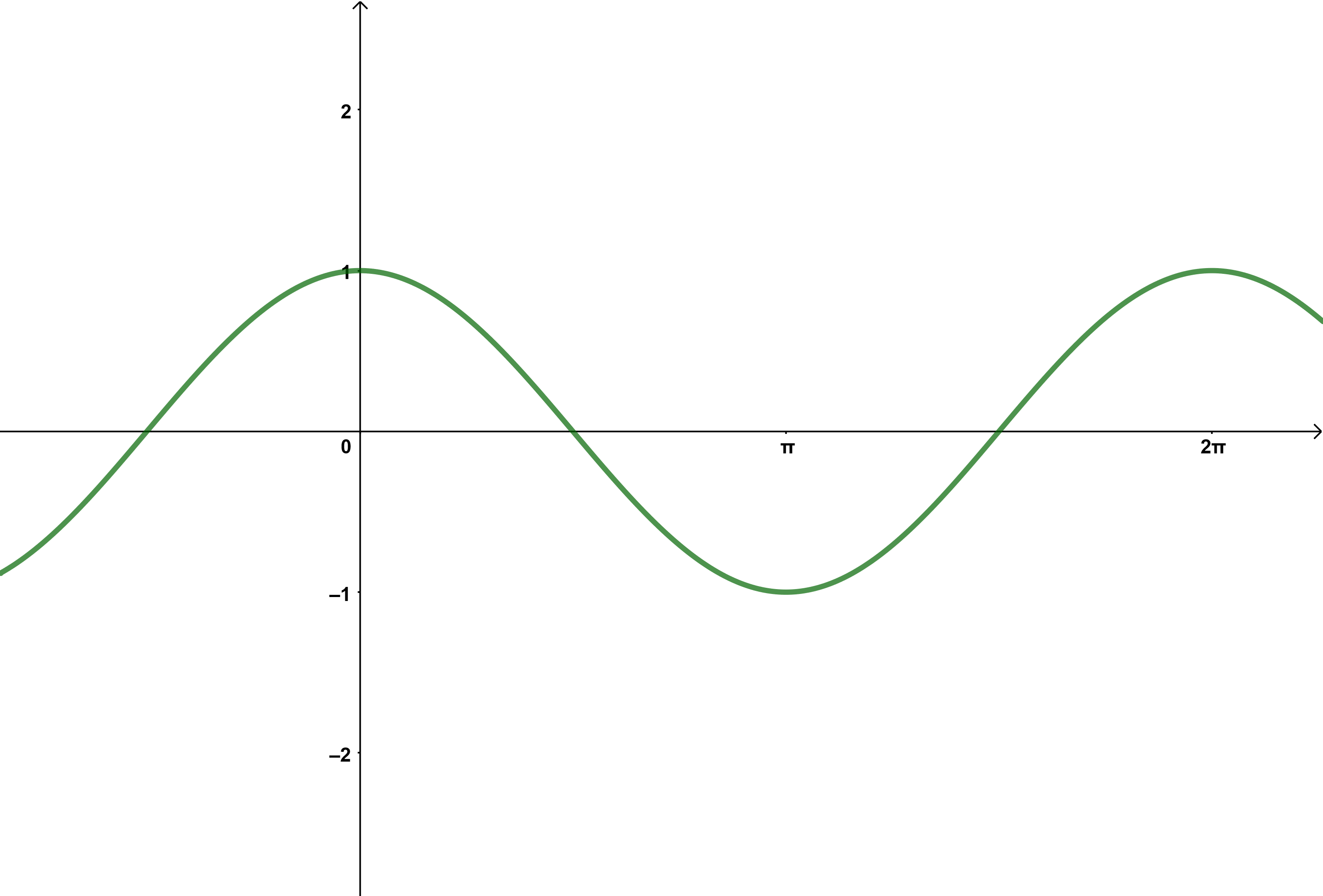
Sinus
Der Funktionsterm lautet
Allgemein lässt sich eine Sinusfunktion mit Streckungen und Verschiebungen durch den Funktionsterm
beschreiben.
Kosinus
Der Funktionsterm lautet
Allgemein lässt sich eine Kosinusfunktion mit Streckungen und Verschiebungen durch den Funktionsterm
beschreiben.
Tangens
Der Funktionsterm lautet
Der Tangens ist definiert durch das Verhältnis der Sinus- und Kosinusfunktion
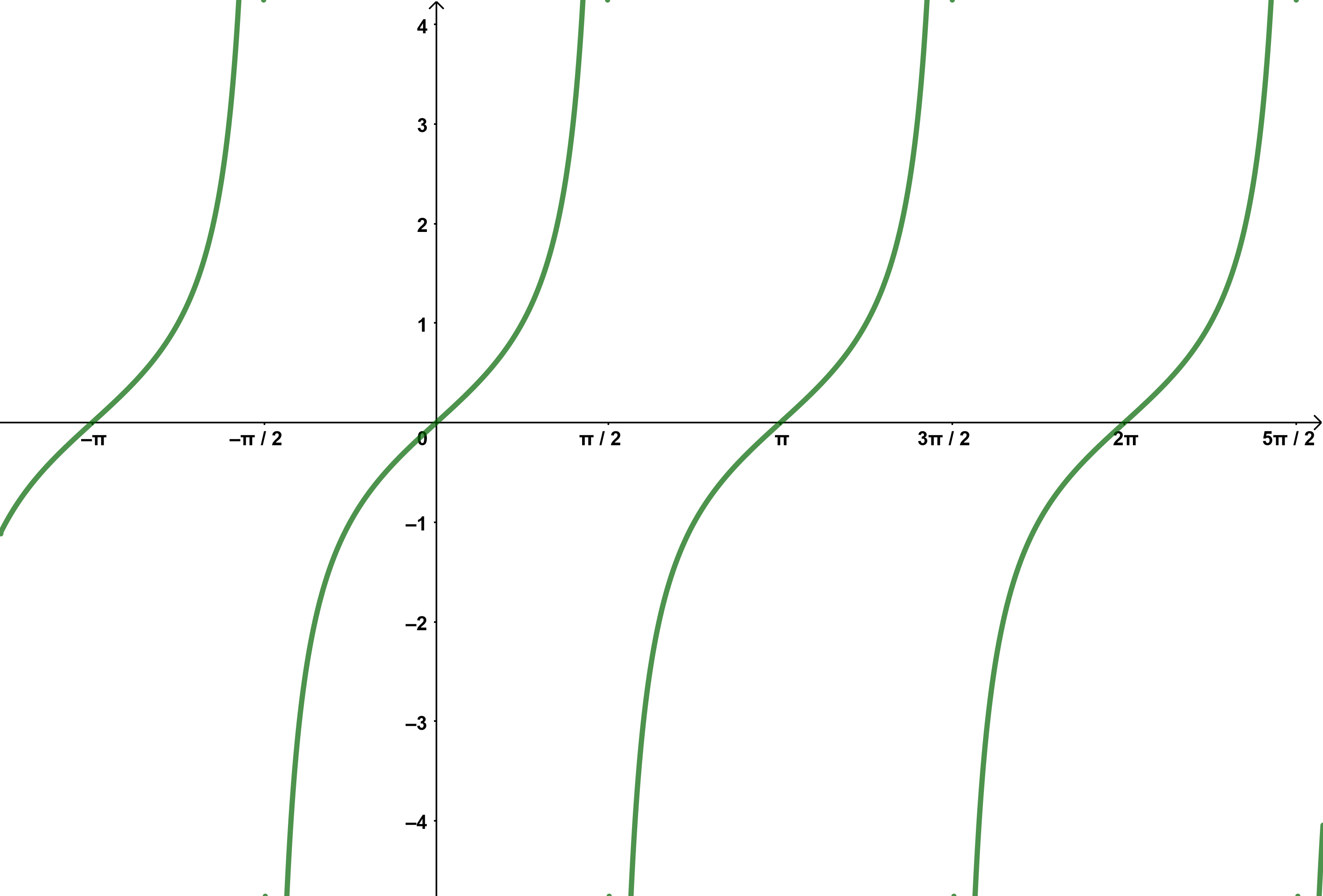
Die Funktion besitzt Definitionslücken im Abstand von aufgrund der Nullstellen des Kosinus.
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
