Logarithmusfunktion

Eine Logarithmusfunktion ist eine Abbildung der Form

f : ℝ^{+} \to ℝ, x \mapsto \log_{b} (x),

wobei $b \in ℝ^{+}$ und $b \neq 1$ gilt.

$b$ heißt Basis des Logarithmus.

Der Logarithmus bezeichnet die Umkehrfunktion der Exponentialfunktion, sodass sich die Funktionen

f (x) = b^{x}, g (x) = \log_{b} (x)

gegenseitig aufheben.

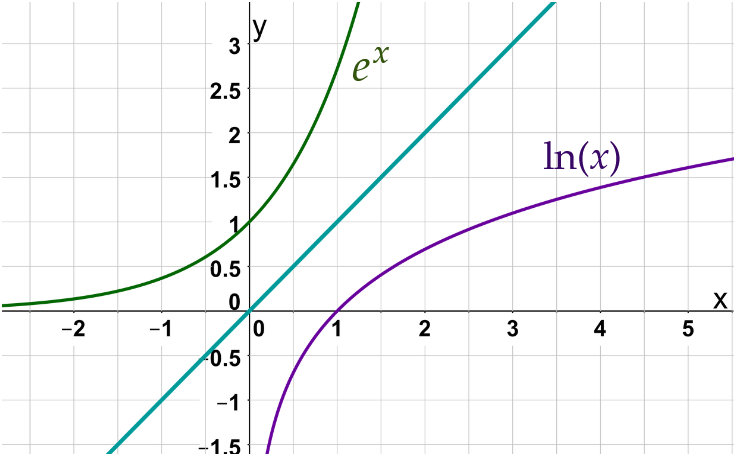
Der Graph der Logarithmusfunktion entsteht durch Spiegelung des Graphen der Exponentialfunktion an der Winkelhalbierenden.

Eigenschaften

Der Definitionsbereich ist $ℝ^{+}$ , d.h. für $x$ dürfen nur positive, reelle Zahlen eingesetzt werden.
Der Wertebereich ist ganz $ℝ$ .
Alle Logarithmusfunktionen haben die Nullstelle $x_{0} = 1$ .
Logarithmusfunktionen haben die $y$ -Achse als senkrechte Asymptote, genauer gilt:
- $b > 1 : \lim_{x \to 0} \log_{b} (x) = - \infty$ und $\lim_{x \to \infty} \log_{b} (x) = \infty$
- $0 < b < 1 : \lim_{x \to 0} \log_{b} (x) = \infty$ und $\lim_{x \to \infty} \log_{b} (x) = - \infty$
Logarithmusfunktionen sind stets monoton, genauer gilt:
- $b > 1 : f$ ist streng monoton steigend.
- $0 < b < 1 : f$ ist streng monoton fallend.

Diese Eigenschaften lassen sich leicht am Graphen der Funktion ablesen:

Mit einem Klick auf Bild oder Button oben stimmst du zu, dass externe Inhalte von GeoGebra geladen werden. Dabei können persönliche Daten zu diesem Service übertragen werden – entsprechend unserer Datenschutzerklärung.

[https://www.geogebra.org/material/iframe/id/2107581]

Benutze den Schieberegler, um die verschiedenen Eigenschaften in Abhängigkeit von der Basis $b$ zu beobachten.

Rechenregeln

Folgende Umformungen sind praktisch, um mit Logarithmen zu rechnen.

$\log_{b} (x \cdot y) = \log_{b} (x) + \log_{b} (y)$
$\log_{b} (\frac{x}{y}) = \log_{b} (x) - \log_{b} (y)$
$\log_{b} (x^{a}) = a \cdot \log_{b} (x)$

Beziehung zu anderen Funktionen

Umkehrfunktion

Die Umkehrfunktion einer Logarithmusfunktion ist eine Exponentialfunktion. Für $f (x) = \log_{b} (x)$ ist die Umkehrfunktion gegeben durch:

f^{- 1} (x) = b^{x}

Durch diese Umkehrfunktion wird auch deutlich, warum sich der Definitionsbereich einer Logarithmusfunktion auf positive Zahlen beschränkt. Schließlich gibt es für ein b>0 kein x, dass

f^{- 1} (x) = b^{x}

negativ werden lässt.

Basiswechsel

Jede Logarithmusfunktion $l o g_{b} (x)$ zu einer beliebigen Basis $b$ (mit $b \in ℝ^{+}$ , $b \neq 1$ ) kann in eine Logarithmusfunktion mit einer anderen Basis $a$ (mit $a \in ℝ^{+}$ , $a \neq 1$ ) umgewandelt werden und andersrum. Die Formel lautet:

\log_{b} (x) = \frac{\log_{a} (x)}{\log_{a} (b)}

Natürliche Logarithmusfunktion

Als Sonderfall eines Basiswechsels kann jede Logarithmusfunktion auf eine natürliche Logarithmusfunktion (auch: $\ln$ -Funktion), d.h. eine Logarithmusfunktion mit Basis $e$ , der Eulerschen Zahl, zurückgeführt werden:

f (x) = \log_{b} (x) = \frac{\ln (x)}{\ln (b)} = \frac{1}{\ln (b)} \cdot \ln (x)

Diese Beziehung ist unter anderem wichtig zur Berechnung der Ableitung und Stammfunktion. Außerdem erkennt man hier, dass jede beliebige Logarithmusfunktion nur ein Vielfaches der $\ln$ -Funktion ist.

Erste Ableitung

Die erste Ableitung von $f (x) = \log_{b} (x)$ ist gegeben durch:

f^{'} (x) = \frac{1}{\ln (b) \cdot x}

Integral

Das erste Integral bzw. eine Stammfunktion $F (x)$ einer Logarithmusfunktion $f (x) = \log_{b} (x)$ ist:

F (x) = \frac{1}{\ln (b)} \cdot (x \ln (x) - x)

Du hast noch nicht genug vom Thema?

Hier findest du noch weitere passende Inhalte zum Thema:

Artikel

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?