Teil A - lernen mit Serlo!

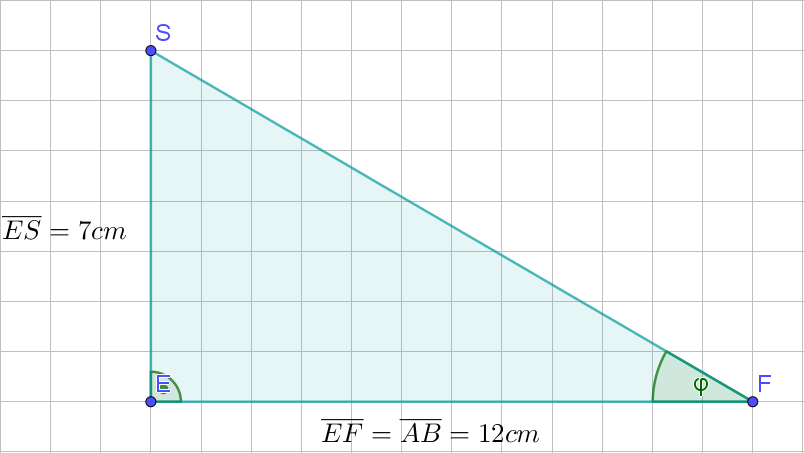
Das Rechteck $A B C D$ mit $A B = 12 cm$ und $B C = 7 cm$ ist die Grundfläche der Pyramide $A B C D S$ (siehe Zeichnung). Die Spitze $S$ liegt senkrecht über dem Mittelpunkt $E$ der Strecke $[A D]$ mit $E S = 7 cm$ . Der Punkt $F$ ist der Mittelpunkt der Strecke $[B C]$ . Runden Sie im Folgenden auf zwei Stellen nach dem Komma.

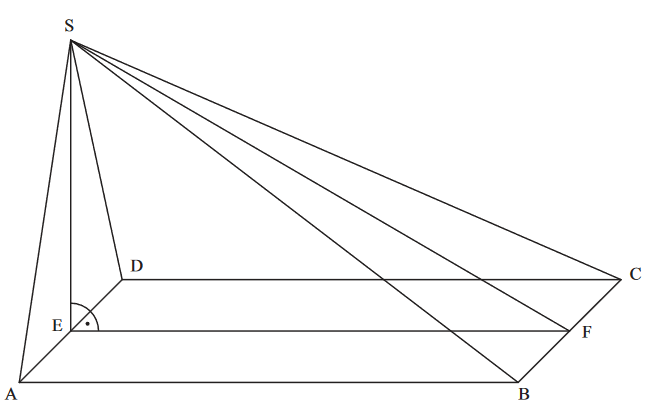
Berechnen Sie das Maß $φ$ des Winkels $S F E$ sowie die Länge der Strecke $[F S]$ .
$[$ Ergebnisse: $φ = {30,26}^{\circ}$ , $F S = 13,89 cm$ $]$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Winkel
Berechnung des Winkels
Zu betrachten ist das Dreieck $S F E$ . Überlege dir welche Seiten gegeben sind und beachte, dass bei $E$ ein rechter Winkel liegt. Daran erkennst du, dass von $φ$ aus betrachtet die Gegenkathete und Ankathete gegeben sind und du den Tangens benötigst, um den Winkel zu berechnen.
$\begin{aligned} \tan φ & = \frac{7}{12} \\ φ & = \tan^{- 1} (\frac{7}{12}) \\ \approx {30,256}^{\circ} \approx {30,26}^{\circ} \end{aligned}$
Berechnung der Streckenlänge
Um die Strecke $[S F]$ zu berechnen benötigst du den Satz des Pythagoras. $[S F]$ liegt dem rechten Winkel gegenüber und ist somit Hypothenuse.
${F S}^{2} = {E S}^{2} + {E F}^{2}$
$\begin{aligned} F S & = \sqrt{{E S}^{2} + {E F}^{2}} \\ = \sqrt{(7 cm)^{2} + (12 cm)^{2}} \\ = \sqrt{193 {cm}^{2}} \approx 13,89 cm \end{aligned}$
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
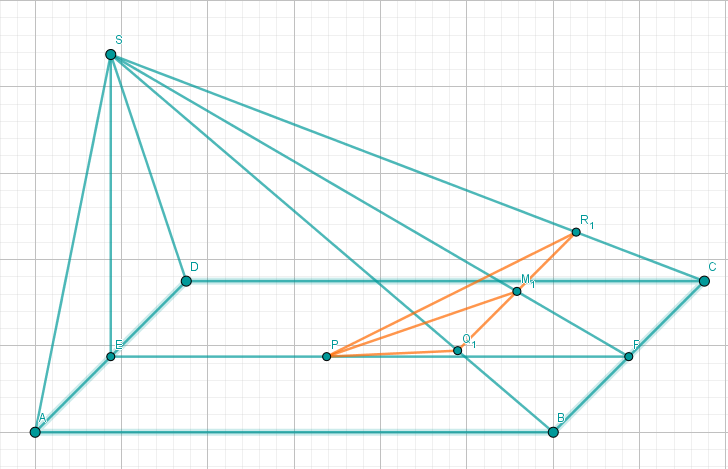
Der Punkt $P$ liegt auf der Strecke $[E F]$ mit $E P = 5 cm$ . Für Punkte $M_{n}$ auf der Strecke $[F S]$ gilt: $F M_{n} (x) = x cm$ mit $x < 13,89$ und $x \in ℝ^{+}$ . Die Punkte $M_{n}$ sind die Mittelpunkte von Strecken $[Q_{n}$ $R_{n}]$ mit $R_{n} \in [C S]$ , $Q_{n} \in [B S]$ und $[Q_{n}$ $R_{n}] | | [B C]$ .
Die Punkte $P$ , $R_{n}$ und $Q_{n}$ sind die Eckpunkte von Dreiecken $P R_{n} Q_{n}$ .
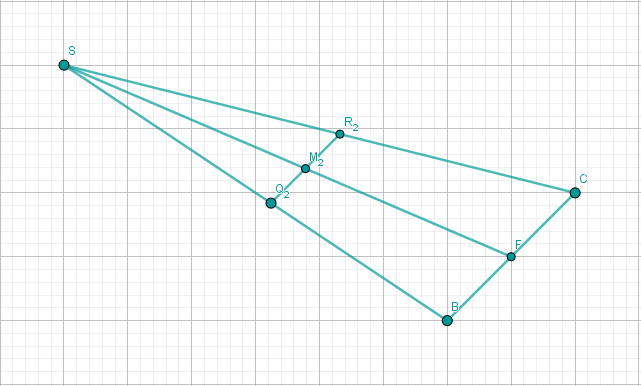
Zeichnen Sie das Dreieck $P R_{1} Q_{1}$ für $x = 3$ in das Schrägbild zu $2 a)$ ein.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Schrägbilder
Zeichnen des Schrägbilds
Zunächst sollte man den Punkt $P$ durch Abmessen einzeichnen. Da sich das Dreieck $S F E$ in der Zeichenebene befindet ( $S$ liegt senkrecht über $E$ ), kann man auch $M_{1}$ durch Abmessen einzeichnen. Laut Angabe ist $F M_{1} = 3 cm$ . Die Strecke $[Q_{1} R_{1}]$ ist parallel zu $[B C]$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
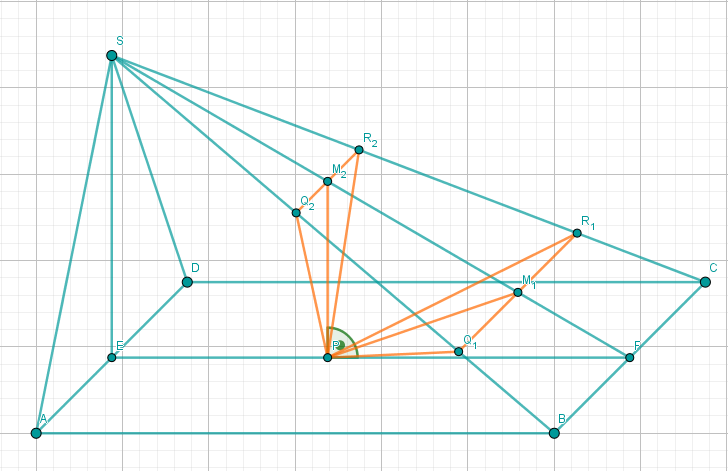
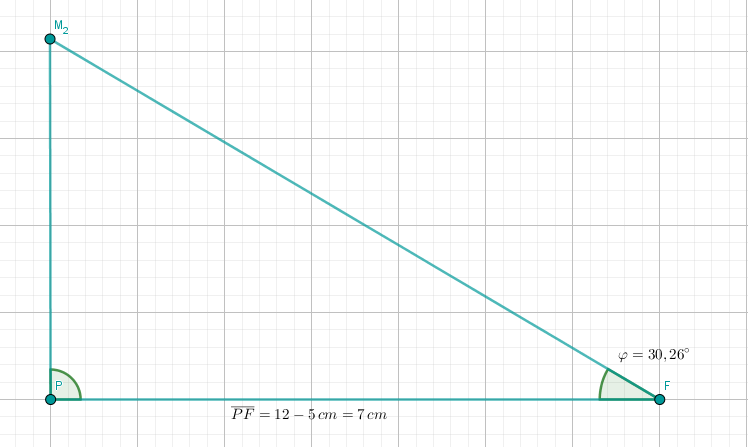
Der Punkt $M_{2}$ auf der Strecke $[F S]$ liegt senkrecht über dem Punkt $P$ . Zeichnen Sie $M_{2}$ und das Dreieck $P R_{2} Q_{2}$ in das Schrägbild zu $2 a)$ ein.
Bestimmen Sie sodann durch Rechnung den zugehörigen Wert für $x$ und die Länge der Strecke $[R_{2} Q_{2}]$ . $[$ Ergebnis: $R_{2} Q_{2} = 2,92 cm$ $]$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Schrägbilder
Dreieck einzeichnen
Wieder gilt, dass das Dreieck $S F E$ in der Zeichenebene liegt. Daher zeichnet man zunächst die senkrechte Strecke $[P M_{2}]$ durch Messung des rechten Winkels ein. $[Q_{2} R_{2}]$ ist wieder parallel zu $[B C]$ .
Gesucht ist die Länge der Strecke $F M_{2} = x$ . Das Dreieck $M_{2} P F$ ist rechtwinklig, außerdem sind die Strecke $P F = 7 cm$ und der Winkel $φ = {30,26}^{\circ}$ gegeben. Die Strecke $[F M_{2}]$ ist dabei die Hypotenuse und somit ergibt sich aus der Formel des Kosinus:
$\cos ({30,26}^{\circ}) = \frac{7 cm}{x}$
$\Rightarrow$ $\begin{array}{l} x = \frac{7 cm}{\cos ({30,26}^{\circ})} \\ \approx 8,10 cm \end{array}$
Streckenlänge berechnen
Um die Länge der Strecke $R_{2} Q_{2}$ zu berechnen, benötigt man den Strahlensatz.
$\frac{R_{2} Q_{2}}{B C} = \frac{S M_{2}}{S F}$
$\frac{R_{2} Q_{2}}{7 cm} = \frac{13,89 cm - 8,10 cm}{13,89 cm}$ | $\cdot 7 cm$
$R_{2} Q_{2} = \frac{5,79 cm \cdot 7 cm}{13,89 cm}$
$R_{2} Q_{2} = 2,92 cm$
Die Länge der Strecke $R_{2} Q_{2}$ ist also $2,92 cm$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Das Dreieck $P R_{2} Q_{2}$ ist die Grundfläche der Pyramide $P R_{2} Q_{2} F$ . Ermitteln Sie rechnerisch den prozentualen Anteil des Volumens der Pyramide $P R_{2} Q_{2} F$ am Volumen der Pyramide $A B C D S$ .

Für diese Aufgabe benötigst Du folgendes Grundwissen: Satz von Pythagoras
Bei dieser Aufgabe sollst du das Volumen der Pyramide $P R_{2} Q_{2} F$ und den prozentualen Anteil des Volumens der Pyramide $P R_{2} Q_{2} F$ zu der Pyramide $A B C D S$ bestimmen.
Das Volumen einer Pyramide bestimmst du durch $V = \frac{1}{3} \cdot G \cdot h$ mit der Grundfläche $G$ und der Höhe $h$ .
Die Grundfläche $G$ ist hier das Dreieck $P R_{2} Q_{2}$ . Die Formel für die Berechnung des Flächeninhalts eines Dreiecks lautet:
$A_{D} = \frac{1}{2} \cdot g \cdot h$
Die Länge der Grundseite $g$ dieses Dreiecks ist gegeben durch $Q_{2} R_{2} = 2,92 cm$ , wie du bereits in Teilaufgabe c) berechnet hast.
Die zweite Größe, die zur Berechnung des Flächeninhalts des Dreiecks nötig ist, ist seine Höhe $\hat{h}$ (Achtung: Hier ist nicht die Höhe $h$ der Pyramide $P R_{2} Q_{2} F$ gemeint, sondern die Höhe $\hat{h}$ des Dreiecks $P R_{2} Q_{2}$ ). Diese Höhe entspricht genau der Länge der Strecke $[M_{2} P]$ . Mithilfe des Satzes von Pythagoras erhältst du:
$M_{2} P = \sqrt{{F M_{2}}^{2} - {P F}^{2}} = \sqrt{(8,1 cm)^{2} - (7 cm)^{2}} \approx 4,08 cm$
Durch Einsetzen der berechneten Größen erhältst du nun für die Grundfläche der Pyramide, die dem Flächeninhalt des Dreiecks entspricht:
$\begin{aligned} G & = \frac{1}{2} \cdot Q_{2} R_{2} \cdot M_{2} P \\ = \frac{1}{2} \cdot 2,92 cm \cdot \sqrt{(8,1 cm)^{2} - (7 cm)^{2}} \\ = \frac{1}{2} \cdot 2,92 cm \cdot 4,08 cm \end{aligned}$
Zur Berechnung des Volumens der Pyramide benötigst du nun noch ihre Höhe $h$ . Diese ist gegeben durch $P F = 7 cm$ .
Für das Volumen der Pyramide $P R_{2} Q_{2} F$ ergibt sich also $\begin{aligned} V & = \frac{1}{3} \cdot G \cdot h \\ = \frac{1}{3} \cdot \frac{1}{2} \cdot 2,92 cm \cdot 4,08 cm \cdot 7 cm \\ = 13,90 {cm}^{3} \end{aligned}$
Für die Pyramide $A B C D S$ ergibt sich $\begin{aligned} V_{A B C D S} & = \frac{1}{3} \cdot G \cdot h \\ = \frac{1}{3} \cdot A B \cdot B C \cdot E S \\ = \frac{1}{3} \cdot 12 cm \cdot 7 cm \cdot 7 cm \\ = 196 {cm}^{3} \end{aligned}$
$\frac{V_{P R_{2} Q_{2} F}}{V_{A B C D S}} = \frac{13,90 {cm}^{3}}{196 {cm}^{3}} = 0,0709$
Der prozentuale Anteil entspricht also $7,09 %$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👇