Teil A

🎓 Prüfungsbereich für Bayern

Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

Die Aufgabenstellung findest du hier zum Ausdrucken als PDF.

1
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
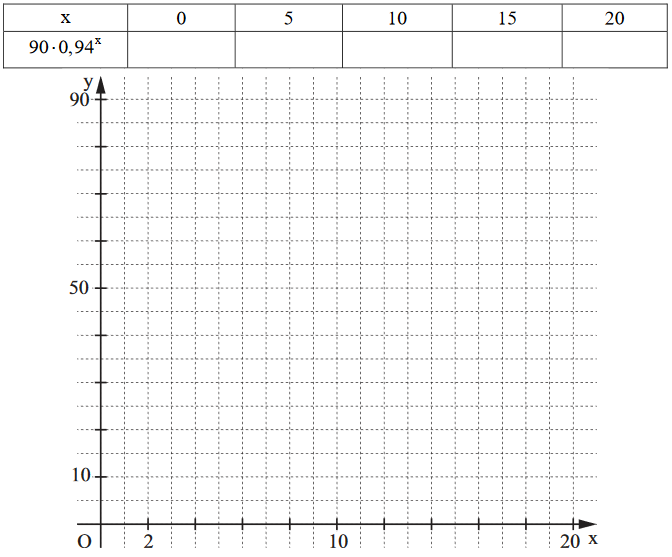
Ein $90^{\circ} C$ heißes Getränk wird zur Abkühlung ins Freie gestellt. Nach $x$ Minuten beträgt die Temperatur des Getränks $y^{\circ} C$ . Die Funktion $f$ mit der Gleichung $y = 90 \cdot {0,94}^{x}$ mit $𝔾 = ℝ_{0}^{+} \times ℝ$ beschreibt näherungsweise den Abkühlvorgang in den ersten $20$ Minuten.
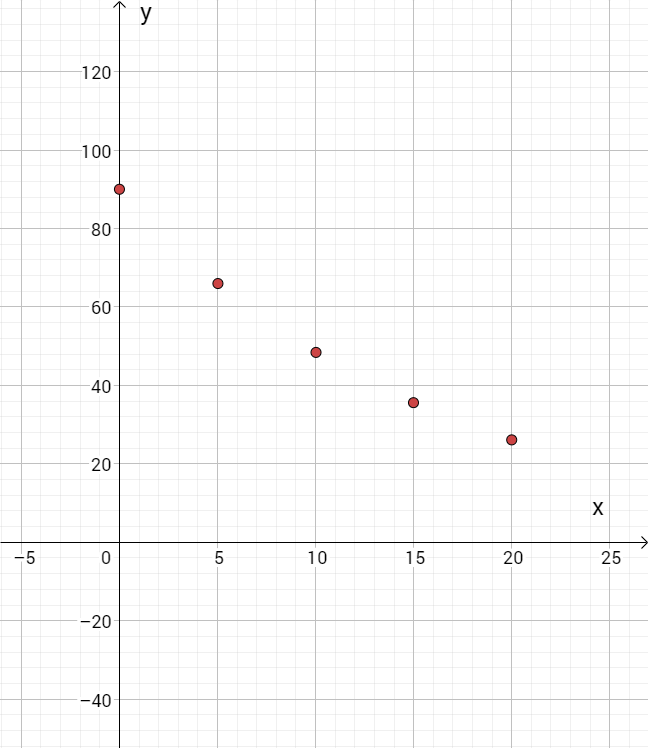
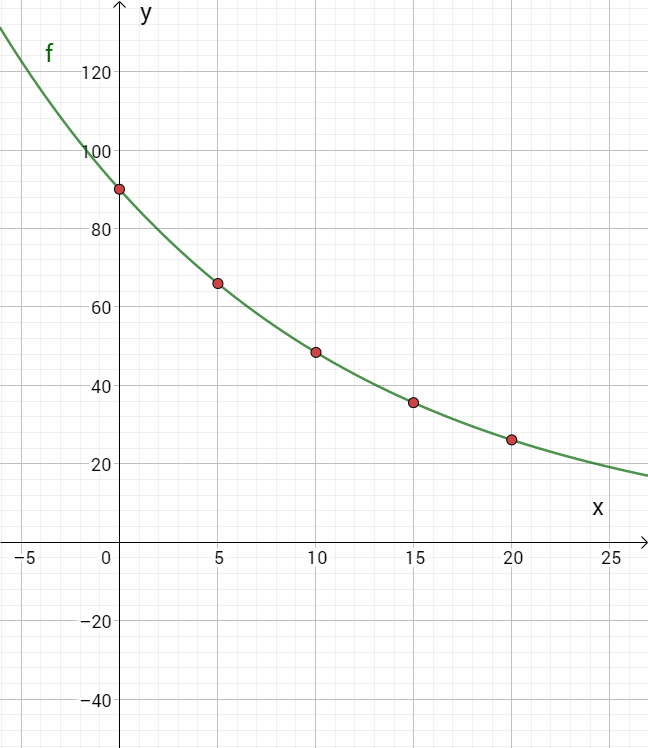
1. Ergänzen Sie die Wertetabelle auf Ganze gerundet und zeichnen Sie sodann den Graphen zu $f$ in das Koordinatensystem ein.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Funktionen zeichnen
  Zeichnen der Funktion
  Die Wertetabelle füllst du aus, indem du die Werte für $x$ in die Funktion $y = 90 \cdot {0,94}^{x}$ einsetzt und den Wert im Taschenrechner berechnest. Anschließend sollst du die Werte noch auf zwei Nachkommastellen runden.
  Du solltest auf die folgenden Ergebnisse kommen:
  Anschließend zeichnest du für jeden Tabelleneintrag einen Punkt in das Koordinatensystem ein. Die $x$ - und $y$ -Werte kannst du direkt ablesen.
  Verbinde diese Punkte anschließend möglichst fließend. Zeichne den Graphen noch ein Stück über den letzten Punkt hinaus!
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Geben Sie an, um wie viel Prozent das Getränk pro Minute kälter wird.
  %
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Exponentialfunktion
  Untersuchung des Wachstumsfaktors
  Aus dem Kapitel zu Exponentialfunktionen weißt du, dass $0,94$ der Wachstumsfaktor der Funktion ist. Da dieser $< 1$ ist, liegt eine Abnahme vor. Das kannst du auch an der Abbildung erkennen. Die Dezimalzahl $0,94$ entspricht $94 %$ . Nach $x$ Minuten beträgt die Temperatur also nur noch $94 %$ der Temperatur, die nach $x - 1$ Minuten gemessen wurde. Sie nimmt also um $6 %$ ab.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
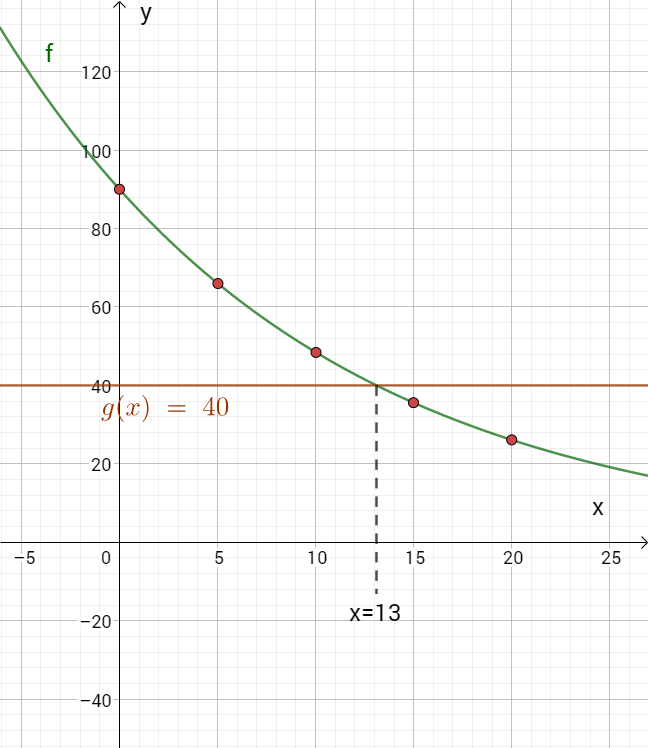
3. Ermitteln Sie mithilfe des Graphen zu $f$ , nach wie vielen Minuten die Temperatur des Getränks noch $40^{\circ} C$ beträgt
  min
  
  Graphische Lösung
  Die Funktion $f (x) = 90 \cdot {0,94}^{x}$ gibt die Temperatur nach $x$ Minuten an. Um die Anzahl an Minuten am Graphen ablesen zu können benötigst du eine Gerade bei $y = 40$ . Dort wo diese deine Funktion $f (x)$ trifft liest du den $x$ -Wert ab. Dieser $x$ -Wert bezeichnet die Anzahl der Minuten.
  Der Schnittpunkt hat den $x$ -Wert $13$ . Somit ist die Temperatur des Getränks nach ca. $13 min$ auf $40^{\circ} C$ abgesunken.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
4. Um wie viel Prozent ist die Temperatur des Getränkes nach sechs Minuten insgesamt gesunken? Kreuzen Sie den zutreffenden Wert an.
  $31 %$
  $36 %$
  $41 %$
  $69 %$
  
  Berechnung des Wachstumsfaktors
  Da die ${0,94}^{x}$ den Wachstumsfaktor nach $x$ Minuten angibt, reicht es, die $6$ für das $x$ einzusetzen. ${0,94}^{6} \approx 0,69$ . Daraus ergibt sich sofort der Wachstumsfaktor $0,69$ , also eine Abnahme um $31 %$ (siehe Teilaufgabe b). Warum ist dies so? Man könnte die Rechnung auch durchführen $f (6) = 90 \cdot {0,94}^{6} \approx 62,09$ . Nach $6$ Minuten beträgt die Temperatur also etwa ${62,09}^{\circ} C$ . Um den prozentualen Anteil auszurechnen, muss man die übrige Temperatur also durch die Anfangstemperatur teilen. $62,09 / 90 \approx 0,69$ . Man multipliziert also anfangs mit der $90$ , später teilt man wieder durch $90$ , um den Wachstumsfaktor auszurechnen, reicht es also ${0,96}^{6}$ zu berechnen.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
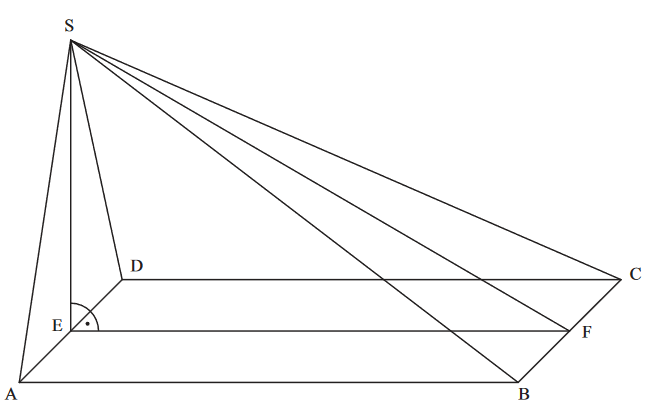
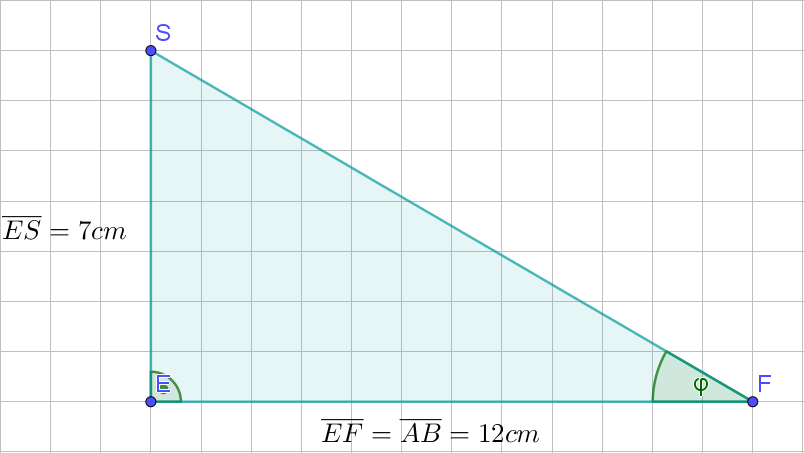
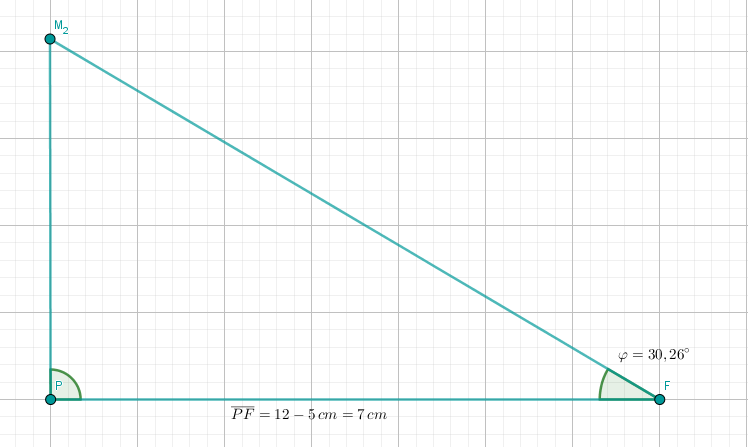
Das Rechteck $A B C D$ mit $A B = 12 cm$ und $B C = 7 cm$ ist die Grundfläche der Pyramide $A B C D S$ (siehe Zeichnung). Die Spitze $S$ liegt senkrecht über dem Mittelpunkt $E$ der Strecke $[A D]$ mit $E S = 7 cm$ . Der Punkt $F$ ist der Mittelpunkt der Strecke $[B C]$ . Runden Sie im Folgenden auf zwei Stellen nach dem Komma.
1. Berechnen Sie das Maß $φ$ des Winkels $S F E$ sowie die Länge der Strecke $[F S]$ .
  $[$ Ergebnisse: $φ = {30,26}^{\circ}$ , $F S = 13,89 cm$ $]$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Winkel
  Berechnung des Winkels
  Zu betrachten ist das Dreieck $S F E$ . Überlege dir welche Seiten gegeben sind und beachte, dass bei $E$ ein rechter Winkel liegt. Daran erkennst du, dass von $φ$ aus betrachtet die Gegenkathete und Ankathete gegeben sind und du den Tangens benötigst, um den Winkel zu berechnen.
  $\begin{aligned} \tan φ & = \frac{7}{12} \\ φ & = \tan^{- 1} (\frac{7}{12}) \\ \approx {30,256}^{\circ} \approx {30,26}^{\circ} \end{aligned}$
  Berechnung der Streckenlänge
  Um die Strecke $[S F]$ zu berechnen benötigst du den Satz des Pythagoras. $[S F]$ liegt dem rechten Winkel gegenüber und ist somit Hypothenuse.
  ${F S}^{2} = {E S}^{2} + {E F}^{2}$
  $\begin{aligned} F S & = \sqrt{{E S}^{2} + {E F}^{2}} \\ = \sqrt{(7 cm)^{2} + (12 cm)^{2}} \\ = \sqrt{193 {cm}^{2}} \approx 13,89 cm \end{aligned}$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
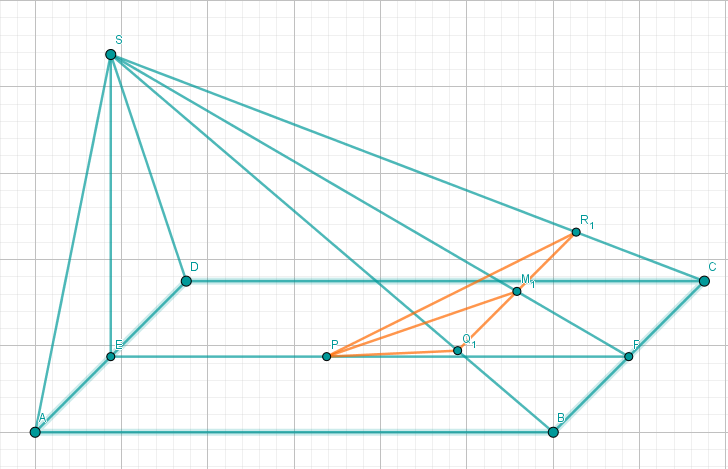
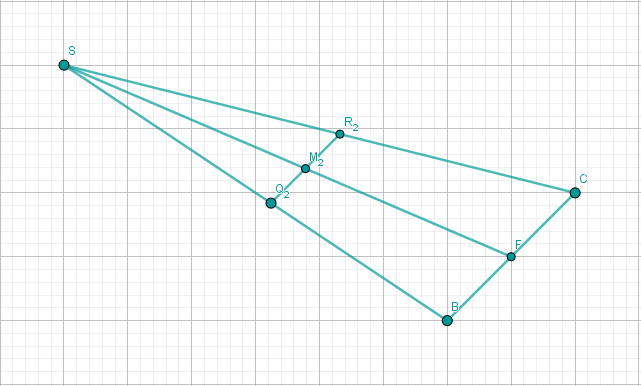
2. Der Punkt $P$ liegt auf der Strecke $[E F]$ mit $E P = 5 cm$ . Für Punkte $M_{n}$ auf der Strecke $[F S]$ gilt: $F M_{n} (x) = x cm$ mit $x < 13,89$ und $x \in ℝ^{+}$ . Die Punkte $M_{n}$ sind die Mittelpunkte von Strecken $[Q_{n}$ $R_{n}]$ mit $R_{n} \in [C S]$ , $Q_{n} \in [B S]$ und $[Q_{n}$ $R_{n}] | | [B C]$ .
  Die Punkte $P$ , $R_{n}$ und $Q_{n}$ sind die Eckpunkte von Dreiecken $P R_{n} Q_{n}$ .
  Zeichnen Sie das Dreieck $P R_{1} Q_{1}$ für $x = 3$ in das Schrägbild zu $2 a)$ ein.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Schrägbilder
  Zeichnen des Schrägbilds
  Zunächst sollte man den Punkt $P$ durch Abmessen einzeichnen. Da sich das Dreieck $S F E$ in der Zeichenebene befindet ( $S$ liegt senkrecht über $E$ ), kann man auch $M_{1}$ durch Abmessen einzeichnen. Laut Angabe ist $F M_{1} = 3 cm$ . Die Strecke $[Q_{1} R_{1}]$ ist parallel zu $[B C]$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
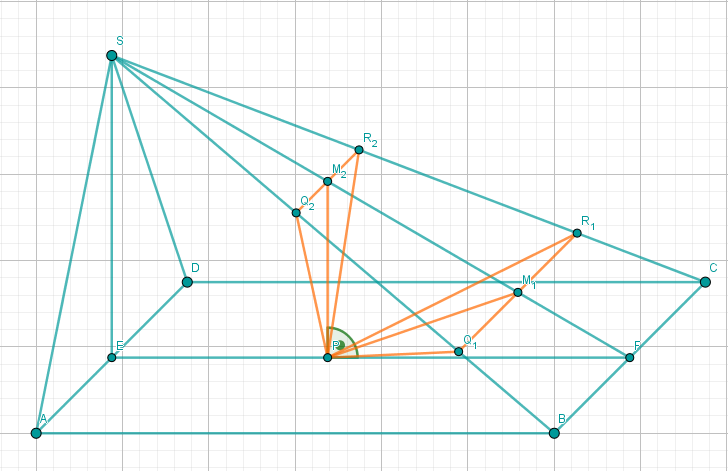
3. Der Punkt $M_{2}$ auf der Strecke $[F S]$ liegt senkrecht über dem Punkt $P$ . Zeichnen Sie $M_{2}$ und das Dreieck $P R_{2} Q_{2}$ in das Schrägbild zu $2 a)$ ein.
  Bestimmen Sie sodann durch Rechnung den zugehörigen Wert für $x$ und die Länge der Strecke $[R_{2} Q_{2}]$ . $[$ Ergebnis: $R_{2} Q_{2} = 2,92 cm$ $]$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Schrägbilder
  Dreieck einzeichnen
  Wieder gilt, dass das Dreieck $S F E$ in der Zeichenebene liegt. Daher zeichnet man zunächst die senkrechte Strecke $[P M_{2}]$ durch Messung des rechten Winkels ein. $[Q_{2} R_{2}]$ ist wieder parallel zu $[B C]$ .
  Gesucht ist die Länge der Strecke $F M_{2} = x$ . Das Dreieck $M_{2} P F$ ist rechtwinklig, außerdem sind die Strecke $P F = 7 cm$ und der Winkel $φ = {30,26}^{\circ}$ gegeben. Die Strecke $[F M_{2}]$ ist dabei die Hypotenuse und somit ergibt sich aus der Formel des Kosinus:
  $\cos ({30,26}^{\circ}) = \frac{7 cm}{x}$
  $\Rightarrow$ $\begin{array}{l} x = \frac{7 cm}{\cos ({30,26}^{\circ})} \\ \approx 8,10 cm \end{array}$
  Streckenlänge berechnen
  Um die Länge der Strecke $R_{2} Q_{2}$ zu berechnen, benötigt man den Strahlensatz.
  $\frac{R_{2} Q_{2}}{B C} = \frac{S M_{2}}{S F}$
  $\frac{R_{2} Q_{2}}{7 cm} = \frac{13,89 cm - 8,10 cm}{13,89 cm}$ | $\cdot 7 cm$
  $R_{2} Q_{2} = \frac{5,79 cm \cdot 7 cm}{13,89 cm}$
  $R_{2} Q_{2} = 2,92 cm$
  Die Länge der Strecke $R_{2} Q_{2}$ ist also $2,92 cm$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
4. Das Dreieck $P R_{2} Q_{2}$ ist die Grundfläche der Pyramide $P R_{2} Q_{2} F$ . Ermitteln Sie rechnerisch den prozentualen Anteil des Volumens der Pyramide $P R_{2} Q_{2} F$ am Volumen der Pyramide $A B C D S$ .
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Satz von Pythagoras
  Bei dieser Aufgabe sollst du das Volumen der Pyramide $P R_{2} Q_{2} F$ und den prozentualen Anteil des Volumens der Pyramide $P R_{2} Q_{2} F$ zu der Pyramide $A B C D S$ bestimmen.
  Das Volumen einer Pyramide bestimmst du durch $V = \frac{1}{3} \cdot G \cdot h$ mit der Grundfläche $G$ und der Höhe $h$ .
  Die Grundfläche $G$ ist hier das Dreieck $P R_{2} Q_{2}$ . Die Formel für die Berechnung des Flächeninhalts eines Dreiecks lautet:
  $A_{D} = \frac{1}{2} \cdot g \cdot h$
  Die Länge der Grundseite $g$ dieses Dreiecks ist gegeben durch $Q_{2} R_{2} = 2,92 cm$ , wie du bereits in Teilaufgabe c) berechnet hast.
  Die zweite Größe, die zur Berechnung des Flächeninhalts des Dreiecks nötig ist, ist seine Höhe $\hat{h}$ (Achtung: Hier ist nicht die Höhe $h$ der Pyramide $P R_{2} Q_{2} F$ gemeint, sondern die Höhe $\hat{h}$ des Dreiecks $P R_{2} Q_{2}$ ). Diese Höhe entspricht genau der Länge der Strecke $[M_{2} P]$ . Mithilfe des Satzes von Pythagoras erhältst du:
  $M_{2} P = \sqrt{{F M_{2}}^{2} - {P F}^{2}} = \sqrt{(8,1 cm)^{2} - (7 cm)^{2}} \approx 4,08 cm$
  Durch Einsetzen der berechneten Größen erhältst du nun für die Grundfläche der Pyramide, die dem Flächeninhalt des Dreiecks entspricht:
  $\begin{aligned} G & = \frac{1}{2} \cdot Q_{2} R_{2} \cdot M_{2} P \\ = \frac{1}{2} \cdot 2,92 cm \cdot \sqrt{(8,1 cm)^{2} - (7 cm)^{2}} \\ = \frac{1}{2} \cdot 2,92 cm \cdot 4,08 cm \end{aligned}$
  Zur Berechnung des Volumens der Pyramide benötigst du nun noch ihre Höhe $h$ . Diese ist gegeben durch $P F = 7 cm$ .
  Für das Volumen der Pyramide $P R_{2} Q_{2} F$ ergibt sich also $\begin{aligned} V & = \frac{1}{3} \cdot G \cdot h \\ = \frac{1}{3} \cdot \frac{1}{2} \cdot 2,92 cm \cdot 4,08 cm \cdot 7 cm \\ = 13,90 {cm}^{3} \end{aligned}$
  Für die Pyramide $A B C D S$ ergibt sich $\begin{aligned} V_{A B C D S} & = \frac{1}{3} \cdot G \cdot h \\ = \frac{1}{3} \cdot A B \cdot B C \cdot E S \\ = \frac{1}{3} \cdot 12 cm \cdot 7 cm \cdot 7 cm \\ = 196 {cm}^{3} \end{aligned}$
  $\frac{V_{P R_{2} Q_{2} F}}{V_{A B C D S}} = \frac{13,90 {cm}^{3}}{196 {cm}^{3}} = 0,0709$
  Der prozentuale Anteil entspricht also $7,09 %$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
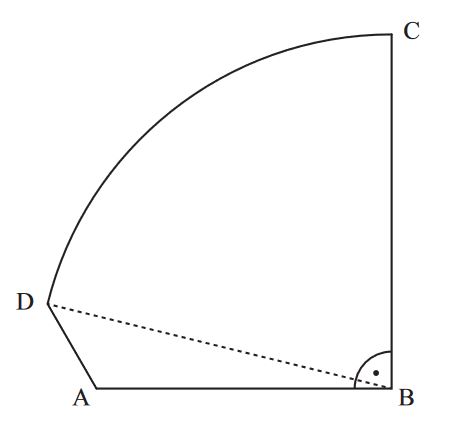
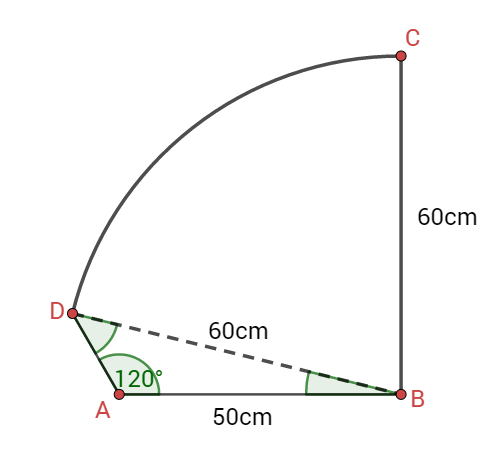
Die Figur $A B C D$ dient als Schnittvorlage für eine Glasscheibe (siehe Skizze).
Der Kreisbogen $C D$ hat den Punkt $B$ als Mittelpunkt und den Radius $r = B C$ . Es gilt:
$A B = 50,0 cm$
$B C = 60,0 cm$
$∢ C B A = 90^{\circ}$
$∢ B A D = 120^{\circ}$
Runden Sie im Folgenden auf eine Stelle nach dem Komma.
1. Berechnen Sie die Länge der Strecke $[D A]$ .
  [Teilergebnis: $∢ D B A = {13,8}^{\circ}$ ; Ergebnis: $[D A] = 16,5 cm$ ]
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Sinussatz
  Berechnung der Strecke $D A$
  Zeichne dir zunächst alle bekannten Größen in die Skizze ein.
  Betrachte anschließend das Dreieck $A B D$ mit den eingezeichneten Winkeln.
  Du kennst bereits die Strecken $A B$ und $B C$ . Außerdem weißt du, dass der Punkt $C$ mit $D$ durch einen Kreisbogen verbunden wird, dessen Mittelpunkt bei $B$ liegt.
  Aus diesem Grund, weißt du, dass der Radius des Kreises $r = B C = 60,0 cm$ gleich lang ist wie $B D$ , da auch das der Radius des Kreises ist.
  Anschließend kannst du über den Sinussatz den Winkel $∢ B D A$ berechnen um dann damit über die Innenwinkelsumme des Dreiecks auf den Winkel $∢ D A B$ zu kommen.
  Stelle den Sinussatz für die Seiten $B D$ und $A B$ und die dazugehörigen Winkel auf.
  $\frac{60,0 cm}{sin (120^{\circ})} = \frac{50,0 cm}{sin (∢ B D A)}$
  Stelle diese Gleichung um, sodass du den Winkel $∢ B D A$ berechnen kannst.
  $\frac{60,0 cm}{sin (120^{\circ})} = \frac{50,0 cm}{sin (∢ B D A)} | \cdot sin (∢ B D A)$
  $\frac{60,0 cm}{sin (120^{\circ})} \cdot sin (∢ B D A) = 50,0 cm | \cdot sin (120^{\circ})$
  $60,0 cm \cdot sin (∢ B D A) = 50,0 cm \cdot sin (120^{\circ}) | : 60,0 cm$
  $sin (∢ B D A) = \frac{50,0 cm}{60,0 cm} \cdot sin (120^{\circ}) | \cdot {sin}^{- 1} (. . .)$
  $∢ B D A = {sin}^{- 1} (\frac{50,0}{60,0} \cdot sin (120^{\circ})) = {46,2}^{\circ}$
  Berechne nun anhand der Innenwinkelsumme von $A B D$ den Winkel $∢ A B D$ .
  $∢ A B D = 180^{\circ} - 120^{\circ} - {46,2}^{\circ} = {13,8}^{\circ}$
  Da du nun alle Winkel und die zwei der drei Strecken kennst, kannst du wiederum über den Sinussatz die Seite $D A$ berechnen.
  $\frac{60,0 cm}{sin (120^{\circ})} = \frac{D A}{sin ({13,8}^{\circ})}$
  Forme diese Gleichung nach der Strecke $D A$ um.
  $\frac{60,0 cm}{sin (120^{\circ})} = \frac{D A}{sin ({13,8}^{\circ})} | \cdot sin ({13,8}^{\circ})$
  $D A = \frac{60,0 cm}{sin (120^{\circ})} \cdot sin ({13,8}^{\circ}) = 16,5 cm$
  Die Strecke $D A$ ist $16,5 cm$ lang.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Die Glasscheibe wird aus einer quadratischen Glasplatte herausgeschnitten. Dazu bewegt sich ein Laserschneider mit einer Geschwindigkeit von $30 cm$ pro Sekunde entlang des Kreisbogens $C D$ und der Strecke $[D A]$ . Berechnen Sie die hierfür benötigte Zeit.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Kreisbogen
  Benötigte Zeit des Laserschneiders
  Der Laserschneider fährt zwei Strecken ab. Einmal die bereits bekannte Strecke $[D A]$ und zum anderen den Kreisbogen von $C$ nach $D$ .
  Aus diesem Grund musst du zuerst diese Strecke herausfinden.
  Dafür benötigst du die Formel für den Kreisbogen.
  $C D = 2 π r \cdot \frac{∢ C B D}{360 °}$
  Den Winkel $∢ D B C$ erhältst du über die Subtraktion des rechten Winkels und des Winkels $∢ D B A$ .
  $C D = 2 π \cdot 60,0 cm \cdot \frac{90^{\circ} - {13,8}^{\circ}}{360 °} = 79,8 cm$
  Addiere die beiden Strecken $C D$ und $D A$ um die gesamte Strecke des Laserschneiders zu bekommen.
  $C D + D A = 79,8 cm + 16,5 cm = 96,3 cm$
  Diese Strecke wird vom Laserschneider in der Geschwindigkeit $v = 30 \frac{cm}{s}$ abgefahren. Stelle die Formel für die Geschwindigkeit ( $v = \frac{s}{t}$ ) nach der Zeit um und setze ein!
  $v = \frac{s}{t} | \cdot t | : v$
  $t = \frac{s}{v}$
  $t = \frac{96,3 cm}{30 \frac{cm}{s}} = 3,2 s$
  Der Laserschneider braucht für diese Strecke $3,2$ Sekunden.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉