Das molare Volumen

Das molare Volumen hängt stark vom Aggregatzustand ab, da Gase im Vergleich zu Feststoffen und Flüssigkeiten ein viel größeres Volumen einnehmen. Das molare Volumen ist vor allem bei Gasen entscheidend, da Gase nicht einfach gewogen werden können. Bei Feststoffen und Flüssigkeiten ist die molare Masse wichtiger. Wenn bei chemischen Reaktionen aus Feststoffen oder Flüssigkeiten Gase entstehen, ist die Volumenzunahme besonders groß. Dies ist zum Beispiel bei Sprengstoffen zu beobachten.

Das molare Volumen ($V_M$) lässt sich berechnen, indem man die molare Masse ($M$) eines Stoffes durch dessen Dichte ($\rho$) teilt. Oder alternativ das Volumen ($V$) eines Stoffes durch die Stoffmenge ($n$).

Das molare Volumen ist von der Temperatur abhängig, da die Teilchenbewegung mit steigender Temperatur zunimmt und diese somit mehr Platz benötigen. Die gleiche Anzahl an Teilchen hat bei einer höheren Temperatur also ein größeres Volumen. Das ist auch der Grund, weshalb sich Stoffe bei Temperaturzunahme ausdehnen (mit wenigen Ausnahmen). Dieses Phänomen wird Wärmeausdehnung genannt.

Molares Volumen von idealen Gasen

Wir beschränken uns hier auf die Betrachtung von idealen Gasen. Bei idealen Gasen gibt es keine Wechselwirkung zwischen den Teilchen, außer wenn diese zusammenstoßen. Die meisten Gase können als ideale Gase betrachtet werden, wenn die Temperatur weit über der Siedetemperatur liegt.

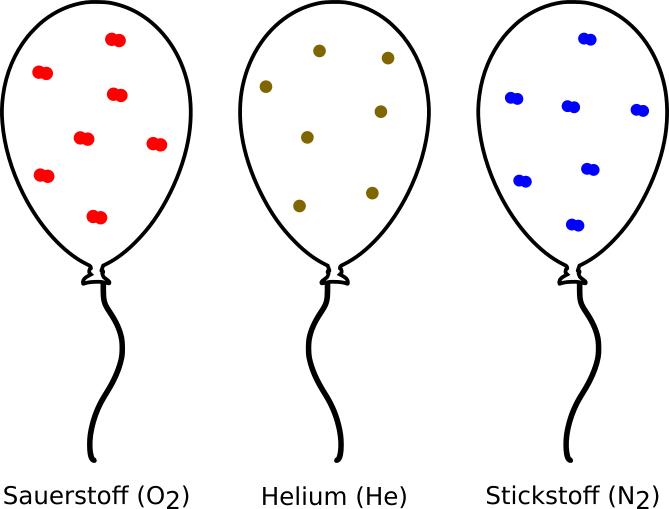
Da es zwischen den Gasteilchen viel leeren Raum gibt, spielt die Größe der Teilchen keine Rolle. Deshalb ist das Volumen, welches von einem Mol eines Gases eingenommen wird, bei allen Gasen gleich. Egal ob Sauerstoff, Stickstoff oder Helium, alle Gase haben bei der gleichen Temperatur das gleiche Volumen.

Das molare Volumen ($V_m)$ von Gasen lässt sich mit der idealen Gasgleichung berechnen:

$V_m = \frac{RT}{p}= \frac{N_Ak_BT}{p}$

Wobei T die Temperatur, p der Druck, R die universelle Gaskonstante, $N_A$ die Avogadrozahl und $k_B$ die Boltzmannkonstante ist.

Unter Standardbedingungen (p = 100'000 kPa, T = 25 °C) beträgt das molare Volumen demnach 24.8 $\frac{l}{mol}$.

Anhand der Gleichung sehen wir auch, dass das molare Volumen von Gasen stark von der Temperatur und dem Druck abhängt.