Definitions- und Wertebereich

1
Aufgaben zum Definitions- und Wertebereich
1. Bestimme den Wertebereich mit dem Definitionsbereich $D_{f} = {ℝ}$ anhand der folgenden Funktionsterme.
  $f (x) = 2 * x^{2}$
  $f (x) = - 5 * x^{2}$
  $f (x) = - 3 * x^{2} + 5$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Definitions- und Wertebereich bestimmen
  An diesem Applet wird der Zusammenhang zwischen Wertebereich und Scheitelpunkt, bzw. dem Parameter a deutlicher, wobei als Definitionsbereich $D_{f} = {ℝ}$ gilt.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Zunächst bestimmst du anhand des Funktionsterms den Scheitelpunkt;
  $f (x) = 2 * x^{2}$ In diesem Funktionsterm ist d = 0, ebenso e = 0. Wir wissen also, dass der Scheitelpunkt den y-Wert 0 hat, der für den Wertebereich relevant ist. Außerdem ist der Parameter a der Funktion positiv, weshalb der Scheitelpunkt ein Tiefpunkt ist. Daher ist der Wertebereich W der Funktion $f (x)$ $W = {y \in ℝ | y \geq 0}$
  $f (x) = - 5 * x^{2}$ Wie im ersten Beispiel ist d = 0, womit der y-Wert des Scheitelpunkts 0 ist . Außerdem ist der Parameter a der Funktion negativ, weshalb der Scheitelpunkt ein Hochpunkt ist. Daher ist der Wertebereich W der Funktion $f (x)$ $W = {y \in ℝ | y \leq 0}$
  $f (x) = - 3 * x^{2} + 5$ In diesem Beispiel ist d=0, aber hier haben wir zusätzlich den Parameter e=5. Wir wissen also, dass der Scheitelpunkt eigentlich den y-Wert 0 hätte. Allerdings besagt der y-Achsenabschnitt, dass zusätzlich 5 addiert werden. Außerdem ist der Parameter a der Funktion negativ, weshalb der Scheitelpunkt ein Hochpunkt ist. Daher ist der Wertebereich W der Funktion $f (x)$ $W = {y \in ℝ | y \leq 5}$
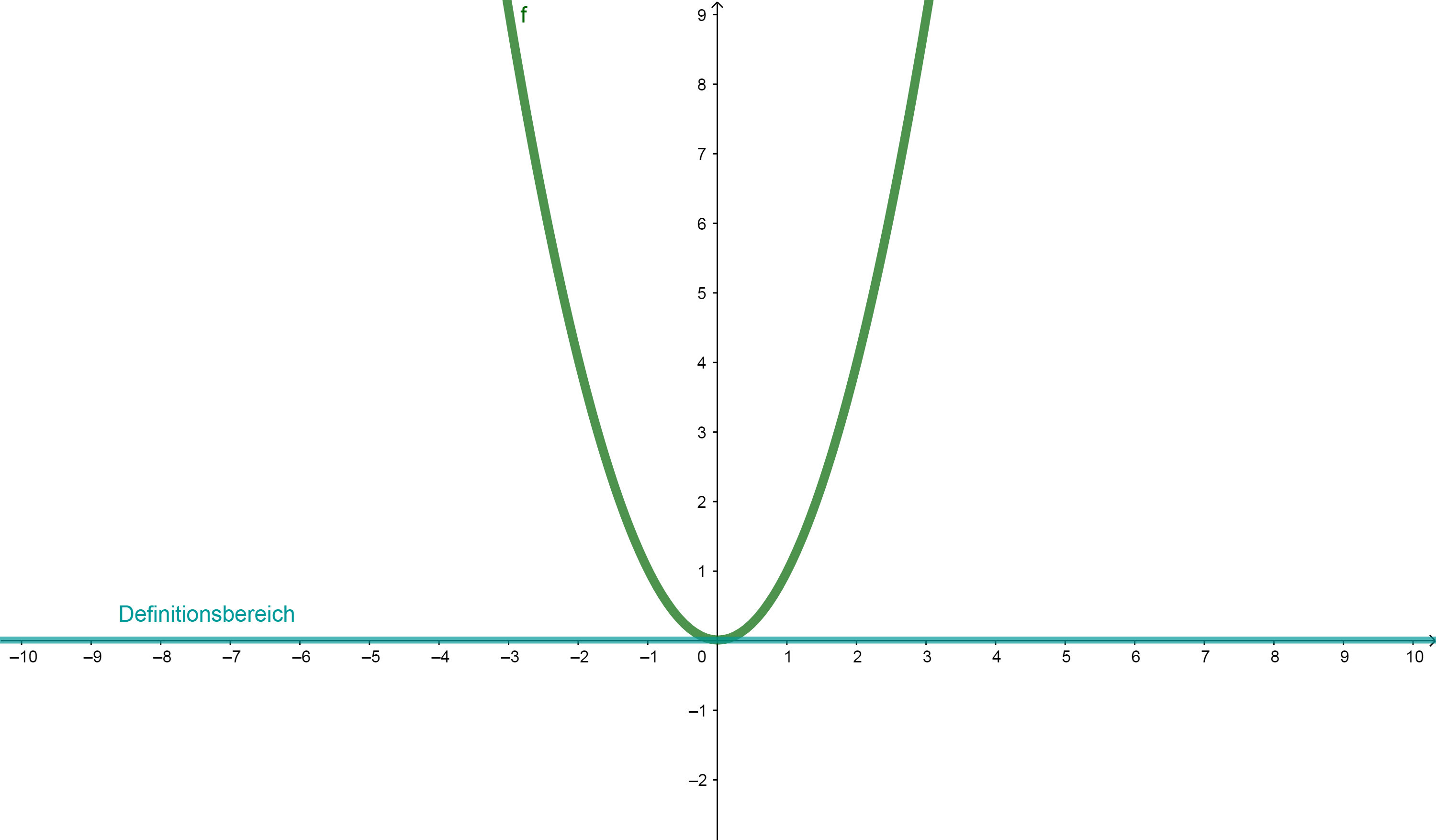
2. Welche Definitionsmenge gilt normalerweise bei quadratischen Funktionen?
  $D_{f} = ℝ$
  $D_{f} = {y \in ℝ | y \geq 0}$
  $D_{f} = {x \in ℝ | x \geq 0}$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Definitionsbereich bestimmen
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Die Definitionsmenge ganz rationaler Funktionen, zu der auch die quadratischen Funktionen gehören, sind immer $ℝ$ , da alle Rechenvorschriften erfüllt werden können und die Zahlenmengen somit nicht eingeschränkt werden müssen.
3. Gib die Wertemenge der quadratischen Funktion bei dem Definitionsbereich $D_{f} = {ℝ}$ an.
  $f (x) = - 2 x^{2} + 8 x - 3$
  $f (x) = 3, 5 x^{2} + 28 x + 57$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Quadratische Gleichungen Umformen
  Nun sieht man sich die quadratische Gleichung erneut an und sucht nach a.
  In dieser Gleichung ist a -2.
  Somit wissen wir, dass der SP ein Hochpunkt ist und deshalb lautet der Wertebereich;
  $W = {y \in ℝ | y \leq 5}$
  2.)
  Zunächst muss der Scheitelpunkt bestimmt werden.
  Dazu muss die Normalform in die Scheitelpunktform überführt werden;
  $f (x) = 3,5 x^{2} + 28 x + 57 |$ Zunächst wird der Koeffizient $3,5$ ausgeklammert
  $f (x) = 3,5 {x^{2} + 8 x} + 57 |$ Nun wird die zweite binomische Formel angewendet
  $f (x) = 3,5 {x^{2} + 2 * 4 * x + 4^{2} - 4^{2}} + 57 |$ Jetzt wird nach der zweiten binomischen Formel zusammengefasst
  $f (x) = 3, 5 {(x + 4) - 4^{2}} + 57 |$ Klammern ausmultiplizieren
  $f (x) = 3, 5 (x + 4) + 1 |$ Scheitelpunkt ablesen
  Scheitelpunkt $f (x) S P (- 4 | 1)$
  Beim erneuten Betrachten der Gleichung zeigt sich, dass der Parameter a positiv ist.
  Somit wissen wir, dass der Scheitelpunkt der Parabel ein Tiefpunkt ist, und deshalb lautet der Wertebereich der Funktion $f (x)$
  $W = {y \in ℝ | y \geq 1}$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  )
  Zunächst muss der Scheitelpunkt bestimmt werden.
  Dazu muss die Normalform in die Scheitelpunktform überführt werden;
  $f (x) = - 2 x^{2} + 8 x - 3 |$ Zuerst wird der Koeffizient -2 ausgeklammert
  $f (x) = - 2 {x^{2} - 4 x} - 3 |$ Nun wird die $2. B i n o m i s c h e F o r m e l$ rückwärts angewendet
  $f (x) = - 2 {x^{2} - 2 * 2 x + 2^{2} - 2^{2}} - 3 |$ Jetzt wird nach der 2. Binomischen Formel zusammengefasst
  $f (x) = - 2 {{(x^{2} - 2)}^{2} - 2^{2}} - 3 |$ Klammern ausmultiplizieren
  $f (x) = - 2 {(x - 2)}^{2} + 5 |$ Jetzt kann man den SP ablesen
  $S c h e i t e l p u n k t f (x) (2 | 5)$
4. Bestimme den Wertebereich der Funktion $f (x) = 5 x^{2} + 30 x + 47$ .
  Beachte hierbei den Definitionsbereich $D_{f} = {- 1, - 2, - 3}$ .
  $W {y \in ℝ | y \leq 2}$
  $W = {2; 5, 20}$
  $W = {2; 22; 7}$
  $W = {2; 7; 22}$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Wertebereich bestimmen
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Zunächst formst du die Normalform in die Scheitelpunktform um.
  Gehe dabei so vor;
  $f (x) = 5 x^{2} + 30 x + 47 |$ $F a k t o r i s i e r e n$
  $f (x) = 5 {x^{2} + 6 x} + 47 |$ $2. B i n o m i s c h e F o r m e l r \ddot{u} c k w \ddot{a} r t s$
  $f (x) = 5 {{(x + 3)}^{2} - 3^{2}} + 47 |$ Klammern ausmultiplizieren
  $f (x) = 5 {(x + 3)}^{2} + 2 |$ Scheitelpunkt ablesen
  $S c h e i t e l p u n k t (- 3 | 2)$
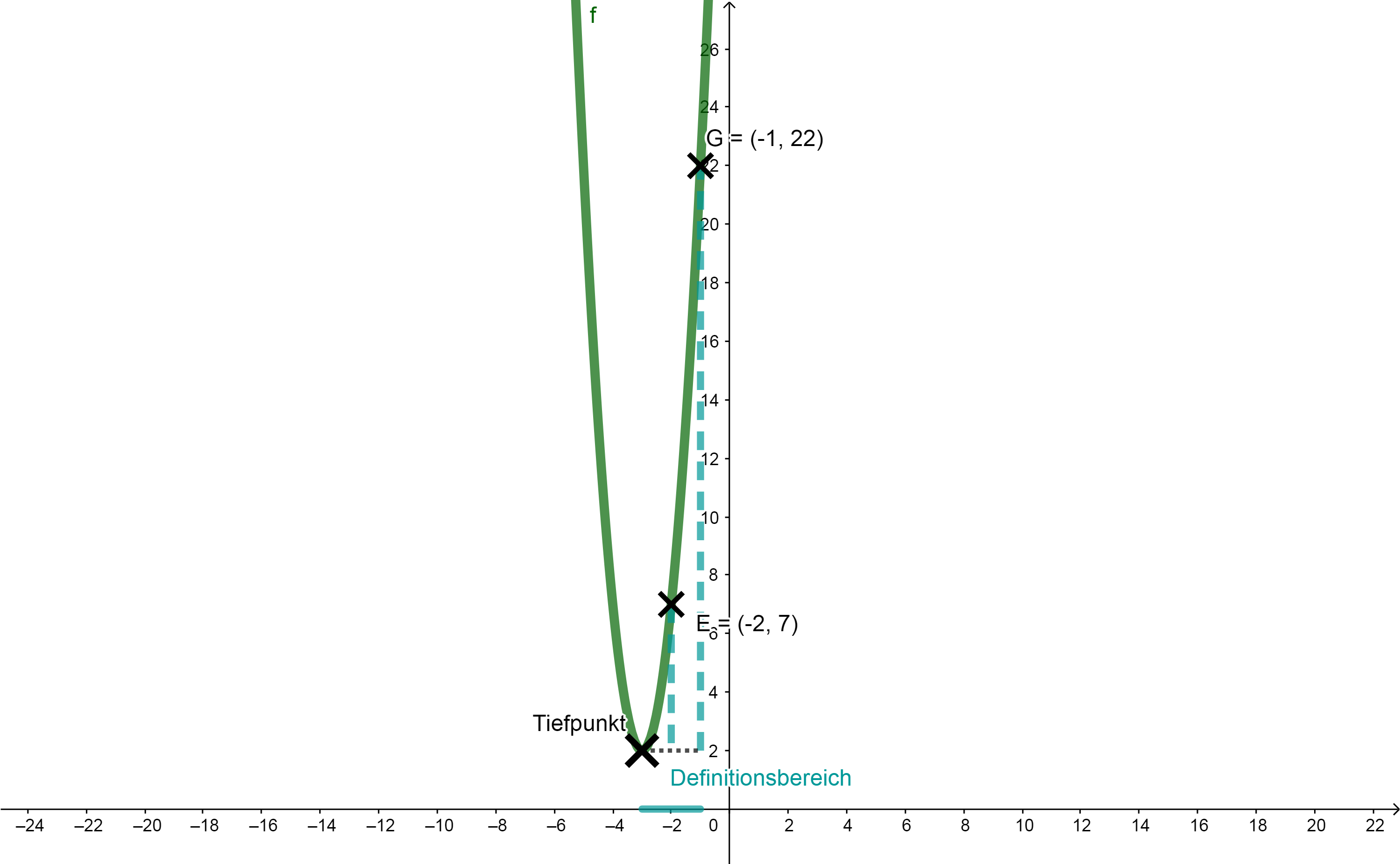
  Nun geht man vom Scheitelpunkt aus eine Einheit nach rechts, wobei man bei -2 landet.
  Nun multipliziert man $- 1^{2}$ mit $5$ . Das Ergebnis ist 5, da die Parabel allerdings um 2 Einheiten nach oben verschoben ist, addiert man 2, sodass man für $f (- 1) = 7$ erhält.
  Nun geht man vom Scheitelpunkt aus zwei Einheiten nach rechts, wobei man bei -1 landet.
  Nun multipliziert man $- 2^{2}$ mit $5$ . Das Ergebnis ist 20, da die Parabel allerdings um 2 Einheiten nach oben verschoben ist, addiert man 2, sodass man für $f (- 2) = 22$
  erhält.
  Somit wurden für die x-Werte -3 (2), -2 (7), und -1(22) eingesetzt und der maximale Definitionsbereich wurde erfüllt.
5. Bestimme den maximalen Definitionsbereich einer Normalparabel anhand folgenden Wertebereichs;
  $W = {4, 16, 25}$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Definitionsbereich bestimmen
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Es stimmt zwar, dass der Wertebereich den Definitionsbereich nicht beeinflusst, man kann jedoch anhand des Wertebereiches den Definitionsbereich ablesen, da spezifische Werte nur bei einem eingeschränkten Definitionsbereich zustande kommen.
  Ist der Definitionsbereich einer Funktion f $D_{f} = {ℝ}$ , so ist der Wertebereich zwar abhängig von dem Scheitelpunkt entweder positiv oder negativ, aber in der Menge umfasst er dementsprechend alle reelen Zahlen.
  Ist der Definitionsbereich eingeschränkt, können auch nur bestimmte x-Werte eingesetzt und "verarbeitet" werden (siehe 1d)).
  Um den maximalen Definitionsbereich von bestimmten y-Werten zu ermitteln, muss man zunächst den Funktionsterm bestimmen, um zu erfahren, in welchem Verhältnis die x- zu den y-Werten stehen.
  In diesem Fall wissen wir, dass es sich um eine Normalparabel mit dem Funktionsterm $f (x) = x^{2}$ handelt.
  Nun rechnet man den jeweils zugehörigen x-Wert aus:
  $D_{f} = {\sqrt{x}, \sqrt{x}; \sqrt{x}}$
  $D_{f} = {\sqrt{4}, \sqrt{16}, \sqrt{25}}$
  $D_{f} = {2, 4, 5}$
  Der Definitionsbereich der Funktion mit dem Wertbereich $W = {4, 16, 25}$ ist also $D_{f} = {2, 4, 5}$ .

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

Definitions- und Wertebereich

Aufgaben zum Definitions- und Wertebereich

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?