Definitions- und Wertebereich

Dieser Artikel befindet sich im Sandkasten und wurde daher nicht auf Korrektheit geprüft! Sieh dir gern den folgenden, geprüften Artikel auf serlo.org an, wenn du mehr zum Thema wissen möchtest: Defintionsbereich und Wertebereich

Der Wertebereich

Der Wertebereich einer quadratischen Funktion gibt alle möglichen y-Werte an, die die Funktion annehmen kann.

Scheitelpunkt bestimmen

Um den Wertebereich einer quadratischen Funktion ermitteln zu können, muss man zunächst feststellen, ob der Scheitelpunkt der Funktion ein Hoch- oder ein Tiefpunkt ist, um zu sehen, ob der Parameter a positiv oder negativ ist.

Parabel der Funktion $f\left(x\right)=a\cdot x^2$

Wertebereich bestimmen

Ist der Scheitelpunkt ein Tiefpunkt, kann die Parabel alle y-Werte annehmen, die größer oder gleich dem y-Wert des Scheitelpunkts sind.

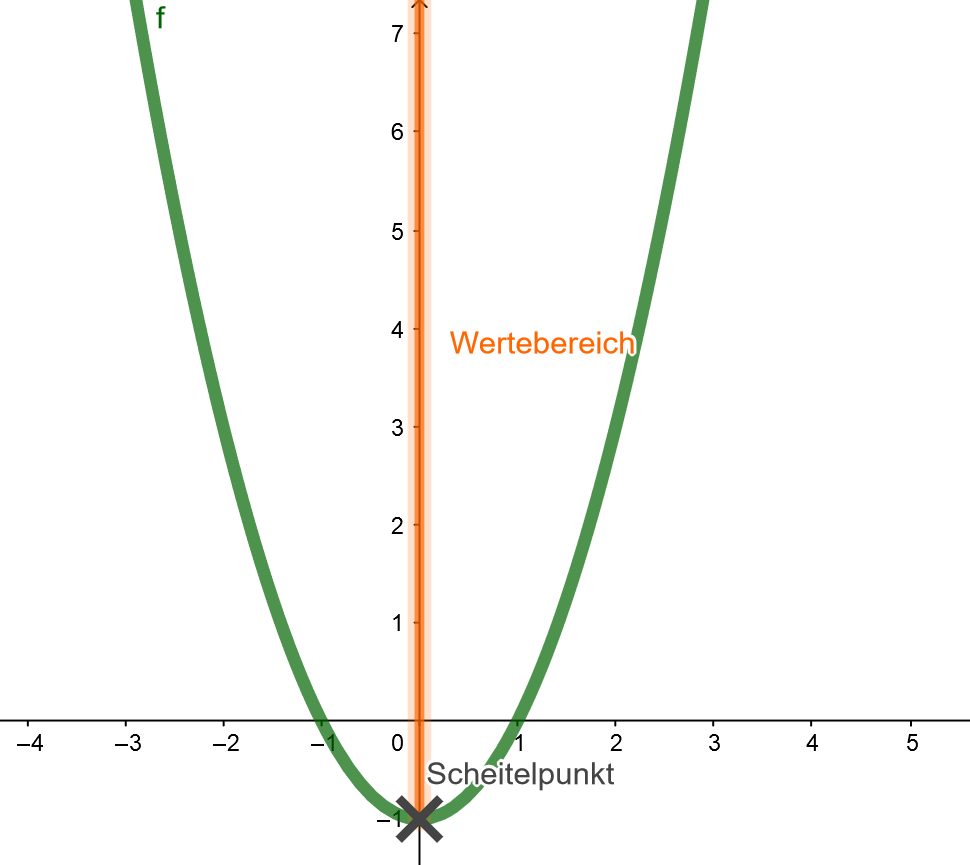
Parabel der Funktion $f\left(x\right)=x^2-1$

Beispiel 1

Der Scheitelpunkt einer Parabel liegt bei (O/-1).

Wir kennen außerdem den Funktionsterm oder können an dem Graphen ablesen, dass der Parameter a größer als 0 ist.

Die Funktion kann demnach nur y-Werte annehmen, die größer oder gleich -1 sind.

Der Wertebereich der Funktion ist

$W=\{y\in ℝ|y\ge -1\}$

Ist der Scheitelpunkt ein Hochpunkt, kann die Parabel alle y-Werte annehmen, die kleiner oder gleich dem y-Wert des Scheitelpunkts sind.

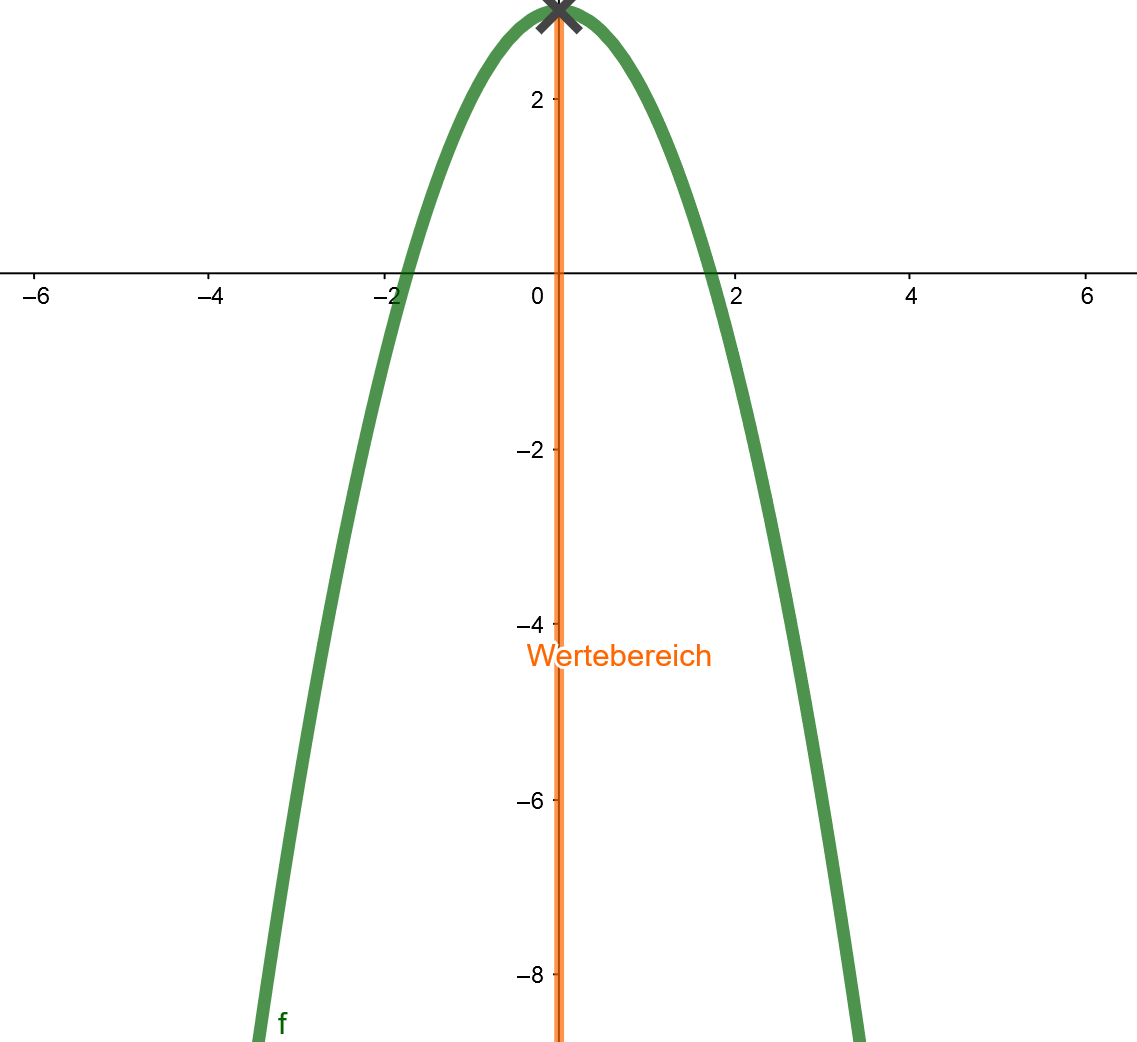
Parabel der Funktion $f\left(x\right)=-x^2+3$

Beispiel 2

Der Scheitelpunkt einer Parabel liegt bei (0/3).

Wir kennen außerdem den Funktionsterm oder können an dem Graphen ablesen, dass der Parameter a kleiner als 0 ist.

Die Funktion kann demnach nur y-Werte annehmen, die kleiner oder gleich 3 sind.

Der Wertebereich der Funktion ist

$W=\{y\in ℝ|y\le 3\}$

Definitionsbereich

Während der Wertebereich einer quadratischen Funktion alle möglichen y-Werte angibt, die die Funktion annehmen kann, gibt der Definitionsbereich alle möglichen x-Werte einer quadratischen Funktion an und wird in einer Funktion f mit $D_f$ bezeichnet.

Bestimmen des Definitionsbereiches

Der Aufgabensteller darf den Definitionsbereich einer quadratischen Funktion beliebig einschränken.

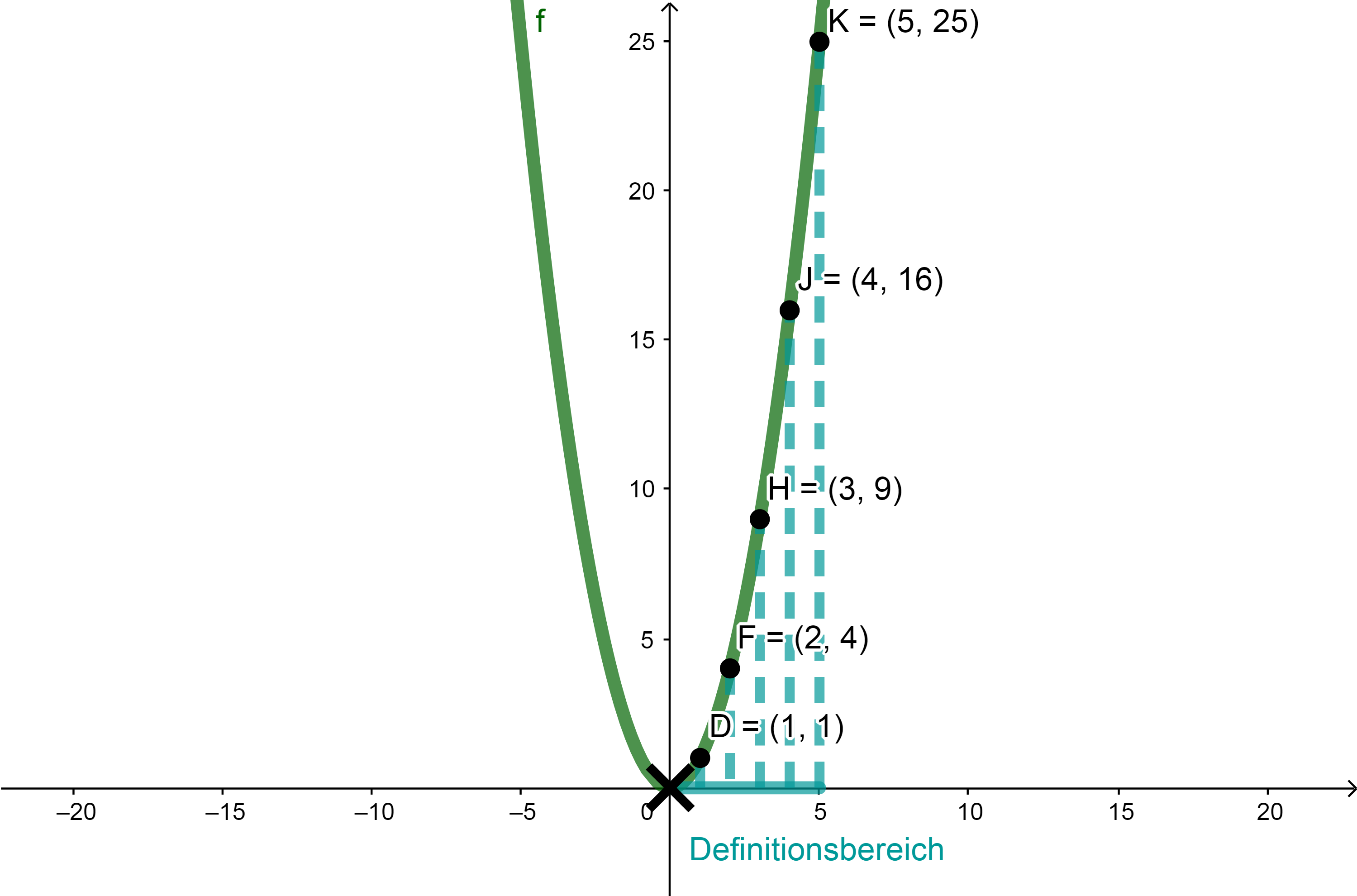
Parabel der Funktion $f\left(x\right)=x^2$ mit dem Definitionsbereich $D_f=\{1,2,3,4,5\}$ und der zugehörigen Wertemenge.

Beispiel 3

$f\left(x\right)=x^2$

$D_f=\left\{\mathrm{1,2,3,4,5}\right\}$

Die Funktion kann also nur die x-Werte 1, 2, 3, 4, 5 annehmen.

Den Maximalen Definitionsbereich bestimmen

Wird in einer Aufgabe gefordert, den Definitionsbereich zu bestimmen, ist damit der maximale Definitionsbereich gemeint, für den die Rechenvorschriften grundsätzlich ausführbar sind.

• Eine Wurzel kann man nur für nicht negative Zahlen ziehen; $f\left(x\right)=\sqrt{x}\to D_f={ℝ}_0^{+}$

Wichtige Zahlenmengen

Anstelle von Reellen Zahlen könne auch andere Zahlenmengen wie Rationale oder Natürliche Zahlen stehen, die ihrerseits eingeschränkt werden können.

• ${ℝ}^{+}=$ alle positiven Zahlen

• ${ℝ}_0^{+}=$ alle nicht negativen Zahlen (alle positiven Zahlen und Null)

Definitionsmenge ganzrationaler Funktionen

Die Definitionsmenge ganzrationaler Funktionen ist immer $ℝ$, da alle Rechenvorschriften erfüllt werden können und die Zahlenmengen nicht eingeschränkt werden müssen.

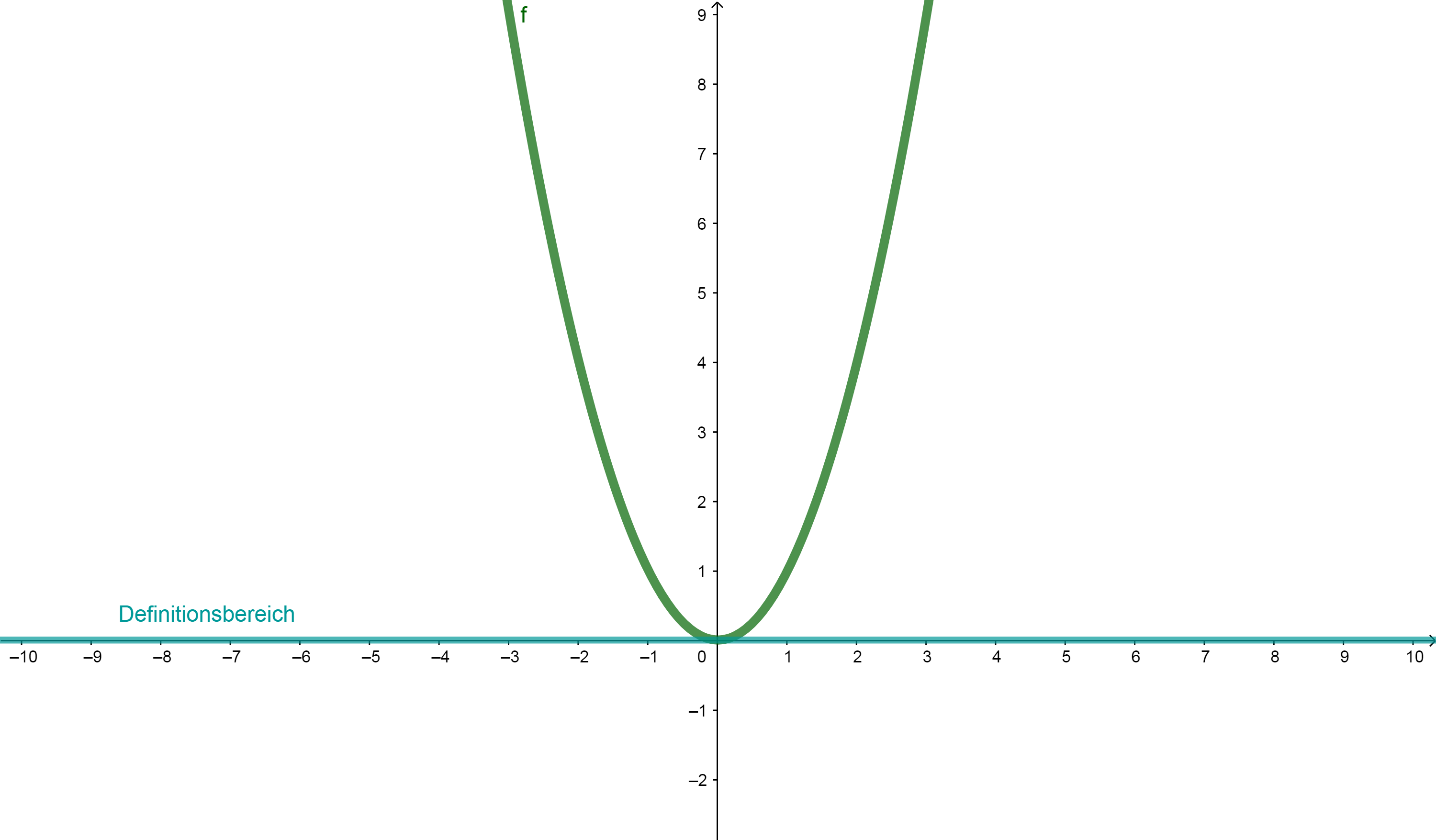
Parabel der Funktion $f\left(x\right)=x^2$

Beispiel 4

$f\left(x\right)=x^2+6x\to D_f=ℝ$

Zusammenhang zwischen Definitions- und Wertebereich

Bestimmt man einen Definitionsbereich, bzw. einen Wertebereich erfolgt dies stets in Abhängigkeit des jeweils anderen.

Beispiel 5

In Beispiel 3 haben wir gelernt, dass der Definitionsbereich vom Aufgabensteller beliebig eingeschränkt werden darf.

Ist der Definitionsbereich einer quadratischen Funktion also $D_f=\{1,2,3,4,5\}$ , kann die Funktion auch nicht eine beliebige Wertemenge haben, auch, wenn es mit einem uneingeschränkten Definitionsbereich so wäre.

Da die Funktion nur die x-Werte 1, 2, 3, 4, 5 annehmen kann, kann man auch nur diese Werte in die Funktion einsetzen.

$f\left(1\right)=1^2\to 1$

$f\left(2\right)=2^2\to 4$

$f\left(3\right)=3^2\to 9$

$f\left(4\right)=4^2\to 16$

$f\left(5\right)=5^2\to 25$

Demnach ist der Wertebereich der Funktion $W=\{1,2,3,4,5\}.$

(Den Graphen mit der Definitions-, bzw. Wertemenge findest du in Beispiel 3.)

Umgekehrt beeinflusst der Wertebereich den Definitionsbereich allerdings nicht, da die y-Werte erst durch die Verarbeitung der x-Werte entstehen.