Dieser Artikel befindet sich im Sandkasten und wurde daher nicht auf Korrektheit geprüft! Sieh dir gern den folgenden, geprüften Artikel auf serlo.org an, wenn du mehr zum Thema wissen möchtest: allgemeine Form und Scheitelform einer quadratischen Funktion
Erklärung:
Die Normalform ist eine quadratische Funktion. Im Gegensatz zur Scheitelform kann man bei ihr den y-Achsenabschnitt direkt ablesen.
Die Formel lautet: 𝑓(𝑥) = 𝑎𝑥² + 𝑏𝑥 + 𝑐
Aufstellung:
Man benötigt den y-Achsenabschnitt (0/c) und zwei weitere gegebene Punkte
Einsetzten des y-Achsenabschnittes in die Normalform
Zwei gegebene Punkte in zwei Gleichungen einsetzen und die Variablen a und b berechnen
Anschließend in die Normalform einfügen
Nullstellenberechnung:
Man kann mit der Normalform die Nullstellen berechnen. Dazu musst du als erstes y gleich null setzen. Anschließend errechnest du die x-Werte für die Nullstellen durch Wurzelziehen. Manchmal ist es nicht direkt möglich die Nullstellen so zu berechnen, dann muss man die pq-Formel anwenden.
Umwandlung in Scheitelform:
|Quadratische Ergänzung |in eine binomische Formel umwandeln
|Scheitelpunkt ablesen
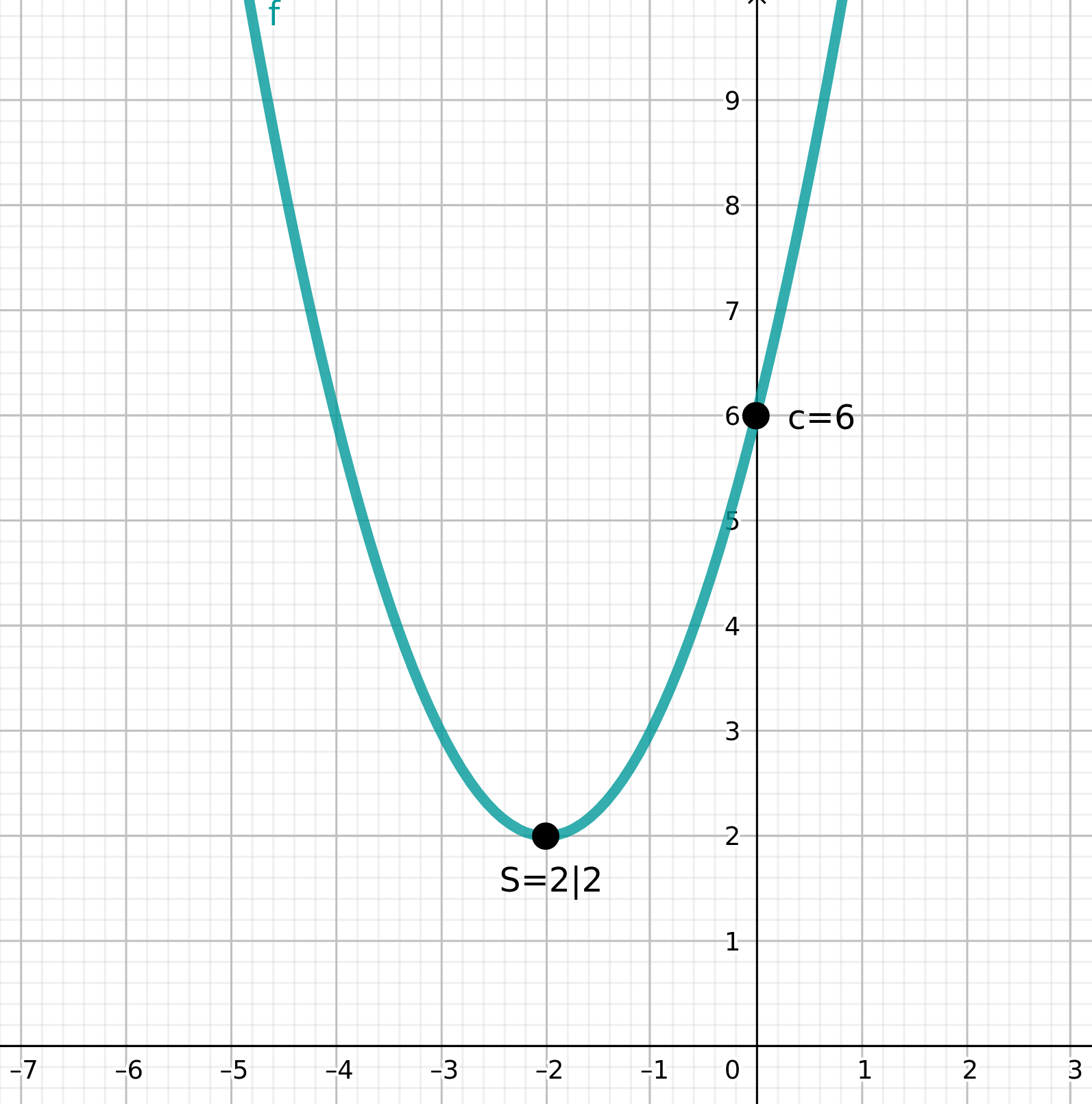
Scheitelpunkt: S=(2|2)

Video zur Umwandlung in die Scheitelform:
Beispielaufgaben:
1) Berechne die Nullstellen indem du die Gleichung 0 setzt:
a)
b)
2) Wandle in die Scheitelpunktform und bestimme den Scheitelpunkt:
a)
b)
