Dieser Artikel befindet sich im Sandkasten und wurde daher nicht auf Korrektheit geprüft! Sieh dir gern den folgenden, geprüften Artikel auf serlo.org an, wenn du mehr zum Thema wissen möchtest: Funktionsterm aufstellen für quadratische Funktionen
Grundwissen:
Um eine quadratische Funktion aufzustellen muss man erst einmal wissen, dass es die Normalform und die Scheitelpunkts-Form gibt und welche Unterschiede diese aufweisen.
Erklärung:
Damit man eine Funktion 2. Grades, also eine Quadratische Funktion, bestimmen/aufstellen kann, benötigt man entweder 3 Punkte (für die Normalform) oder den Scheitelpunkt (S) und einen weiteren Punkt (für die Scheitelpunkts-Form), um die Variablen zu bestimmen.
Beispiel (Normalform):
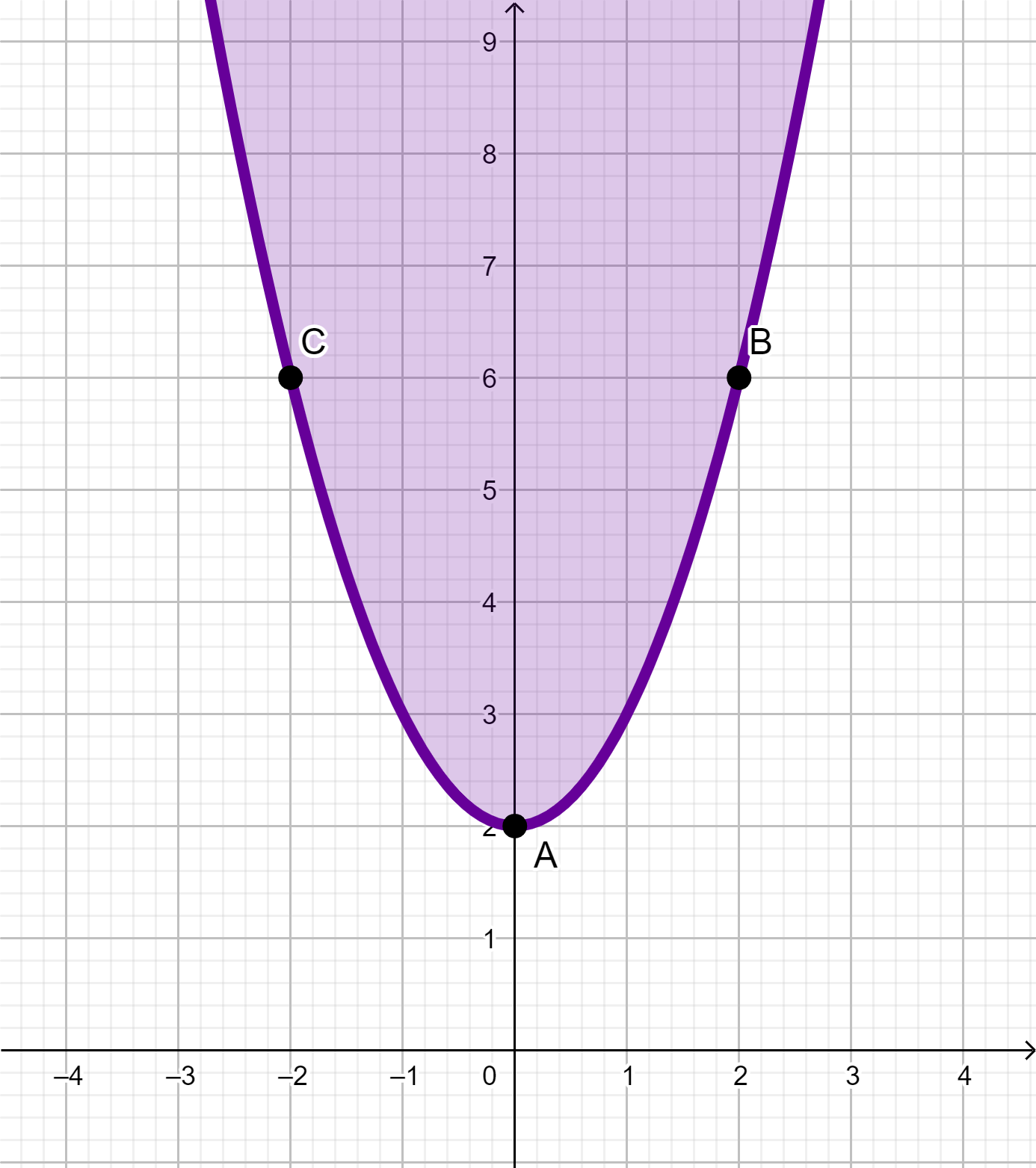
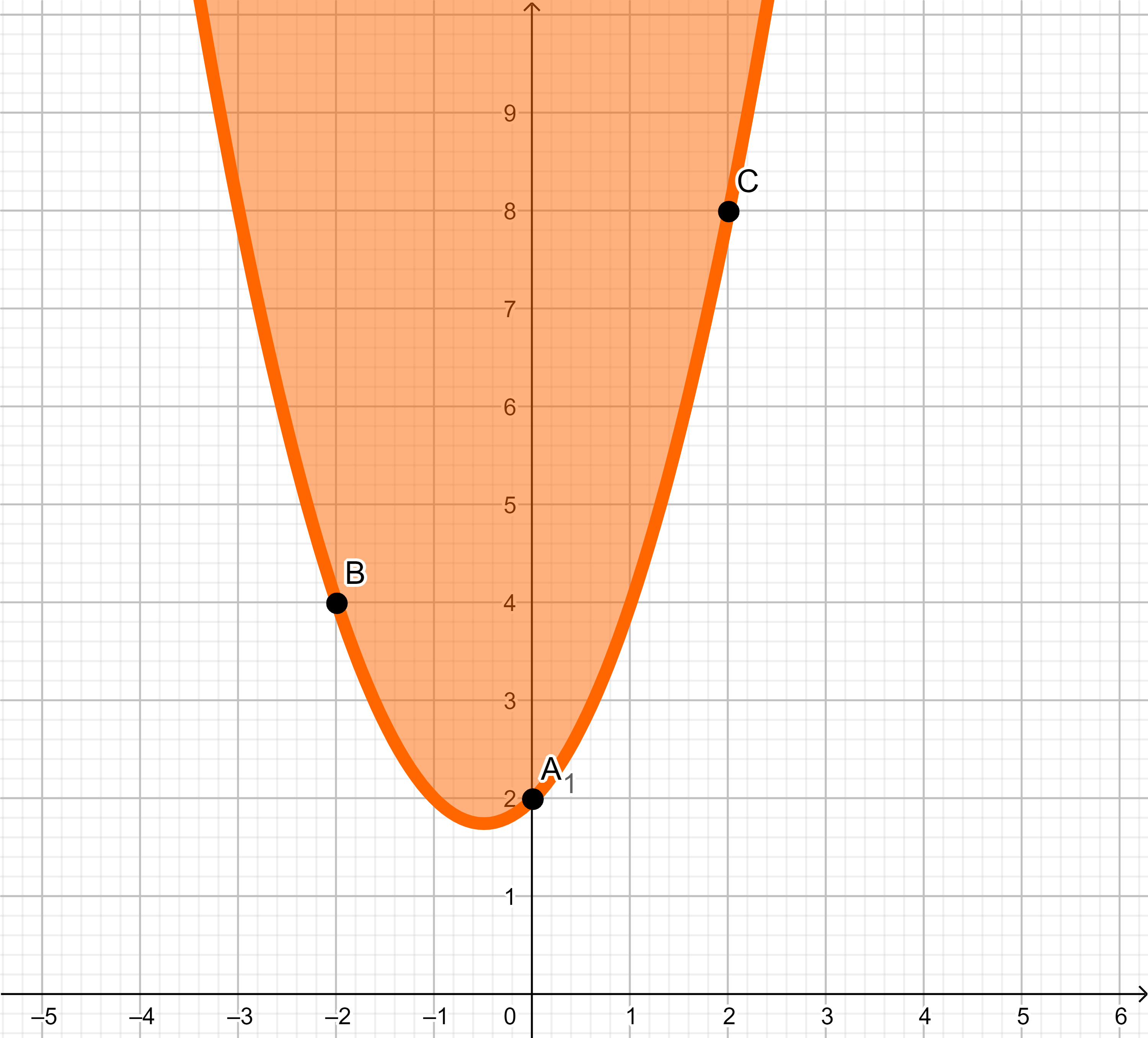
Man kann hier rechts eine „einfache“ Parabel erkennen.
Nun muss man bei dieser Parabel 3 Punkte finden.
Um durch eine Rechnung die Variablen auszurechnen.
Hier sind es die Punkte:
A: (0|2)
B: (2|6)
C: (-2|6)
Damit lassen sich diese Gleichungen aufstellen:
Erster Rechenschritt:
Zuerst rechnen wir die rechte Seite jeder Gleichung aus:
Zweiter Rechenschritt:
Als nächstes rechnen wir den y-Achsenabschnitt aus, also die Variable c:
Zum Glück hat der erste Punkt eine x-Koordinate von 0.
Somit bleibt beim Ausrechnen der ersten Gleichung c=2 übrig.
Damit können wir c=2 in jede Gleichung einsetzen und müssen jetzt einfach die Äquivalenz Umformung anwenden, um die Gleichungen später mit dem Additionsverfahren zu addieren und somit eine weitere Variable weg zu bekommen, aber dazu später mehr…
Dritter Rechenschritt:
Nun formen wir die dritte Formel so um, dass wir danach im Additionsverfahren das a wegbekommen. Wir rechnen die Gleichung also *(-1):
Damit können wir die zweite Formel und diese umgeformte dritte Formel im Additionsverfahren untereinanderschreiben und das b ausrechnen:
b ist gleich 0
Vierter Rechenschritt:
Jetzt müssen wir das b in eine Gleichung einsetzten (hier: die 2.) und das a ausrechnen:
a=1
Letzter Schritt:
Nur noch schnell die Probe machen, indem wir alle Variablen in eine der Gleichungen einsetzten:
und fertig.
Beispiel anhand der Scheitelpunkts-Form:
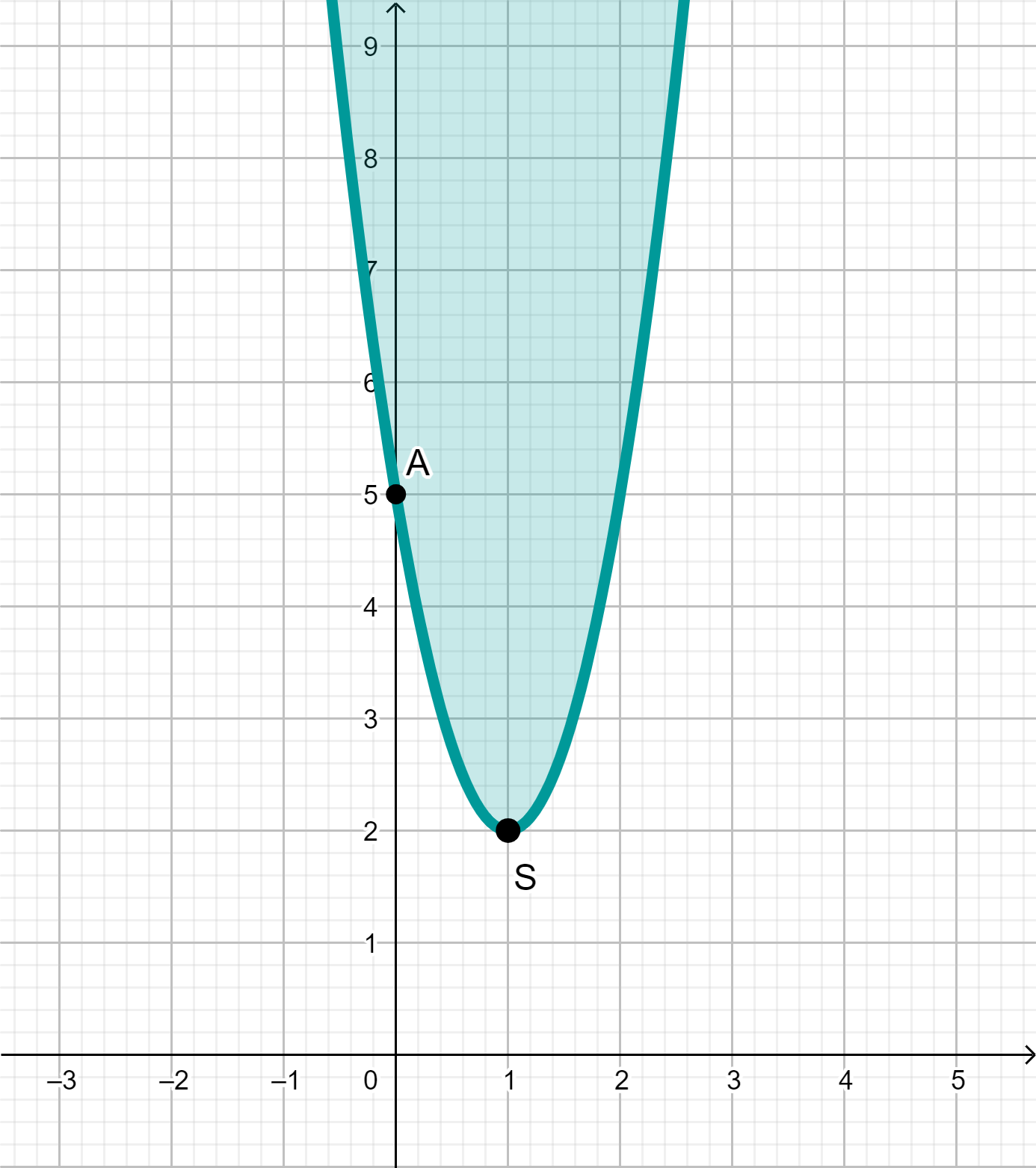
Hierfür brauchen wir den Scheitelpunkt der Parabel auf der rechten Seite:
S=(1|2)
Und einen weiteren Punkt, um die Variable a auszurechnen:
A=(0|5)
Bei dieser Form ist das aufstellen der Funktions-Gleichung einfacher und schneller, als bei der anderen.
Also denk dran: Wenn du den Scheitelpunkt hast brauchst du keine Normalform bestimmen.
Zuerst setzten wir S in die Gleichung der Scheitelpunkts-Form ein:
Erster Schritt:
Nun müssen wir nur noch den Punkt einsetzten:
Zweiter Schritt:
Und jetzt einfach ausrechnen:
So sehen wir, dass „a“ gleich 3 ist.
Letzter Schritt:
Nochmal die Probe machen, also a in die Anfangsgleichung einsetzten:
Und fertig.
Teste dich!
Aufgabe 1)
Stelle die
Funktionsgleichung
in Normalform und
Scheitelpunkts-Form
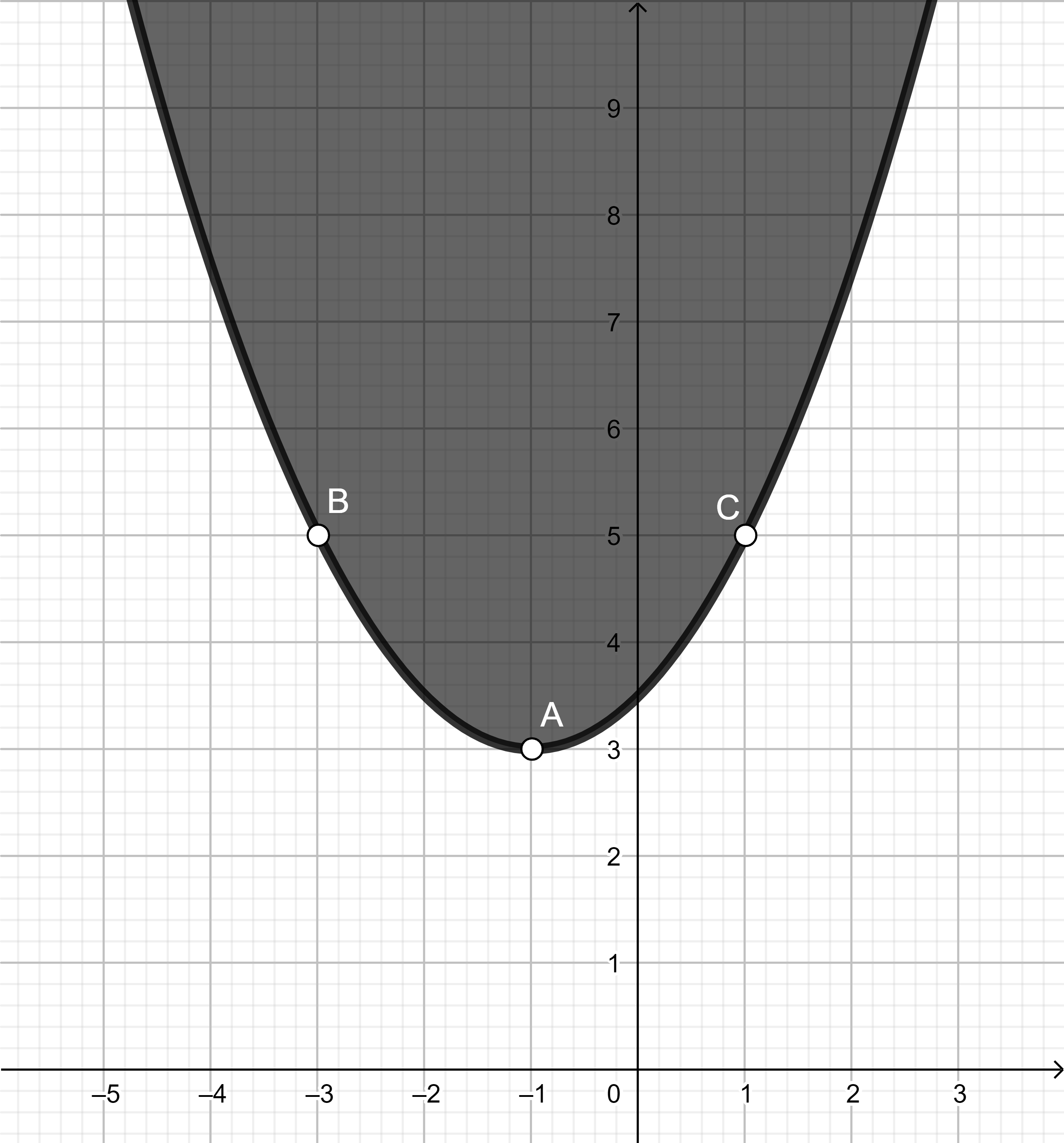
zu dieser Parabel auf.
Bevor ich dir die Lösung verrate kannst du in diesen GeoGebra-Applets die Schieberegler so verschieben, das deine Werte jeweils für „a, b und c“ und für „a, d und e“ dort angegeben sind und sie dir die Parabel anzeigen. Die richtige Parabel ist die Abbildung 3.
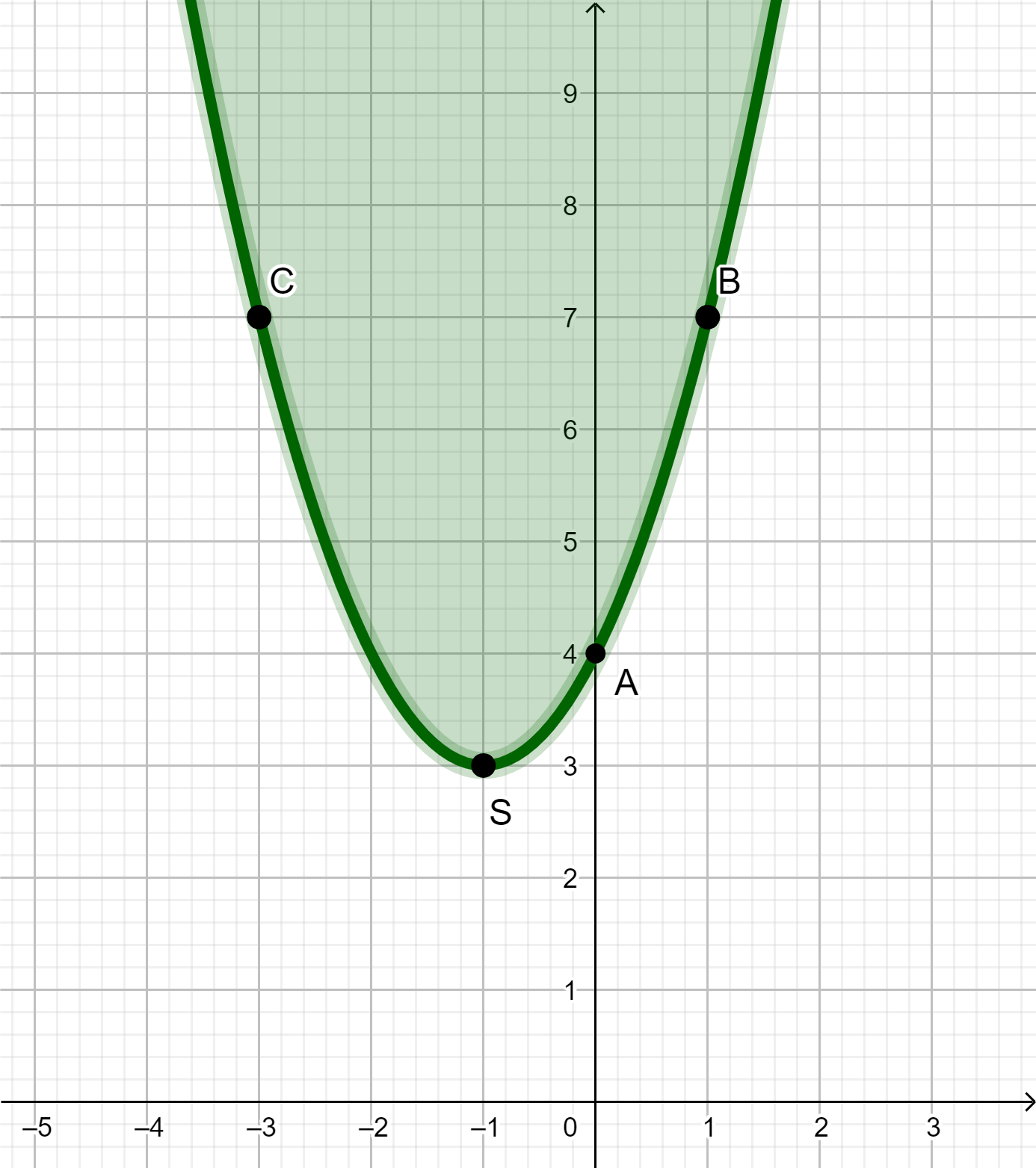
Aufgabe 2)
Suche dir aus, welche Parabel du wie ausrechnest. Achte dabei, wo es besser ist die Scheitelpunkts-Form zu nehmen und benutze insgesamt beide Formen.
Entscheide, welche Form du benutzt.
Lies die Punkte bei beiden Parabeln ab.
Stelle Gleichungen auf.
Rechne die Variablen aus.
Mache eine Probe.