In diesem Kurs lernst du die Schiefe Ebene kennen, welche Kräfte an ihr wirken und durch welche Formeln die Bewegungen auf ihr beschrieben werden können.

Vorwissen

• Kraft (Grundlagen)

• Beschleunigung (Grundlagen)

• Sinus, Kosinus und Tangens

Kursdauer

ca. 60 min, inklusive Experiment

Eine Schiefe Ebene ist nichts anderes als z.B. ein Brett, das schief steht. Eine Kugel auf ihr würde herunterrollen oder ein Spielzeugauto herunterfahren. Wir gehen in diesem Kurs davon aus, dass keine Reibung stattfindet.

Bildquelle: Rhetos, CC0 1.0, Wikimedia

Bildquelle: Klaus-Dieter Keller, CC0 1.0, Wikimedia

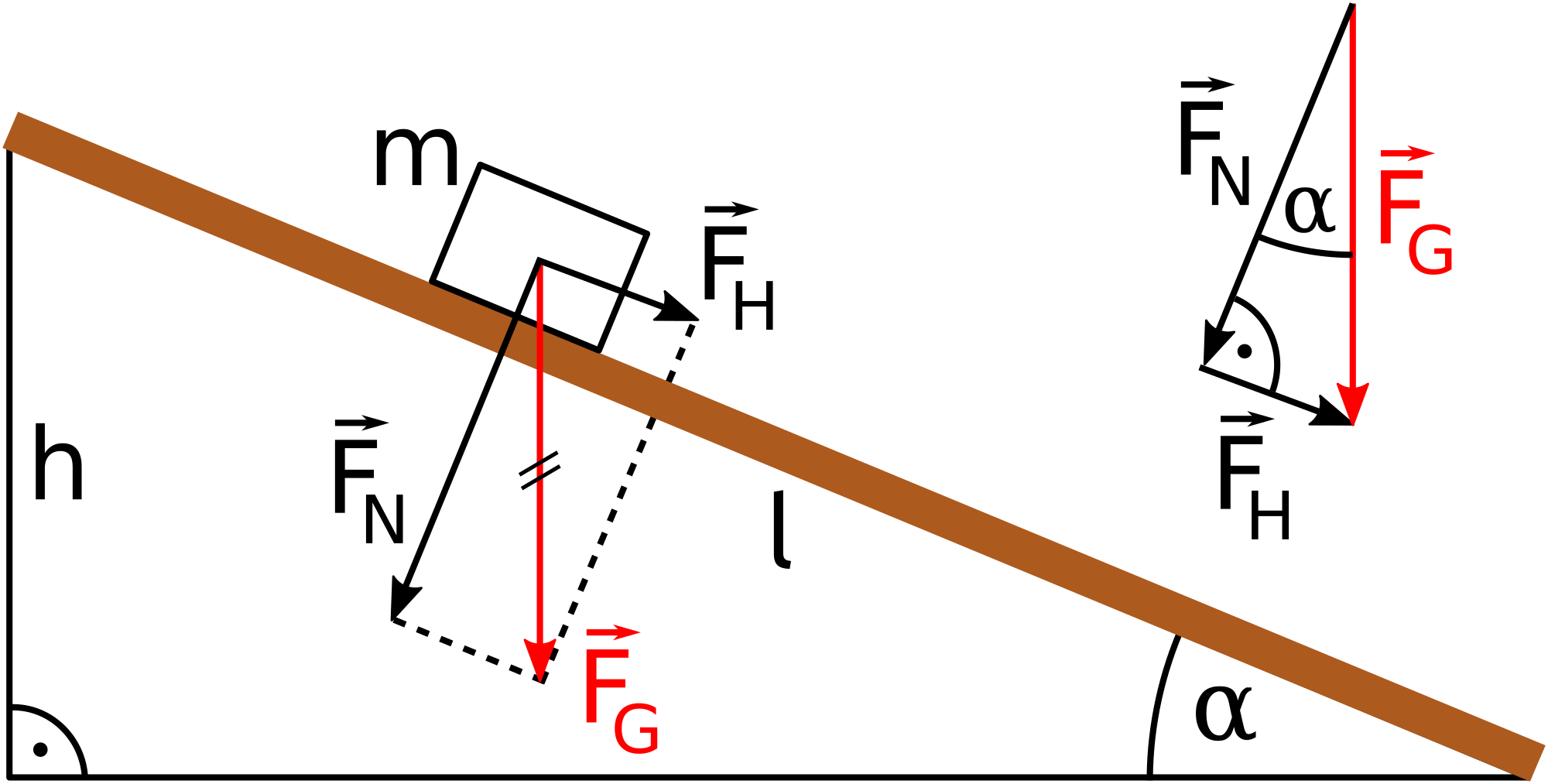
Das Brett hat die Länge $ll$ und wird an einer Seite um die Höhe $hh$ angehoben. Dies ergibt einen Neigungswinkel $\alpha \backslash alpha$ zur Horizontalen. Auf dem Brett liegt ein Körper mit der Masse $mm$.

Im großen rechtwinkligen Dreieck gilt mit den Regeln für Sinus, Kosinus und Tangens

$\sin \alpha =\frac{h}{l}\backslash sin\backslash alpha=\backslash frac\{h\}\{l\}$ Das nennen wir Gleichung $(1)(1)$.

Würde das Brett flach auf dem Boden liegen ($\alpha =0\mathrm{°}\backslash alpha=0°$), wäre die Gewichtskraft ${\vec{F}}_G\backslash vec\{F\}\_\{G\}$ des Körpers senkrecht zum Brett gerichtet. Da das Brett aber jetzt geneigt ist, wirkt auch die Gewichtskraft schräg auf das Brett. Man zerlegt die Gewichtskraft in zwei Komponenten: Eine parallel und eine senkrecht zum Brett.

• Die parallele Komponente heißt Hangabtriebskraft ${\vec{F}}_H\backslash vec\{F\}\_\{H\}$. Sie beschleunigt den Körper. Dies wird später noch wichtig.

• Die senkrechte Komponente heißt Normalkraft ${\vec{F}}_N\backslash vec\{F\}\_N$. Sie führt zur Reibung mit dem Brett, die wir in diesem Kurs ja vernachlässigen wollen.

Man schreibt vektoriell

${\vec{F}}_G={\vec{F}}_N+{\vec{F}}_H\backslash vec\{F\}\_G=\backslash vec\{F\}\_N+\backslash vec\{F\}\_H$

Vergleiche dazu das kleine Dreieck rechts oben: Statt vom Beginn zum Ende des roten Pfeils direkt zu gehen, kommt man am gleichen Ziel heraus, wenn man die zwei schwarzen Pfeile hintereinander läuft.

Die Gewichtskraft ${\vec{F}}_G\backslash vec\{F\}\_\{G\}$ wird durch die zwei Komponenten ${\vec{F}}_H\backslash vec\{F\}\_\{H\}$ und ${\vec{F}}_N\backslash vec\{F\}\_\{N\}$ ersetzt. Damit man nicht denkt, dass an der Masse nun drei Kräfte wirken, streicht man den Vektorpfeil der Gewichtskraft durch.

Wenn du am blauen Punkt die Neigung veränderst, ändern sich auch die zwei Komponenten.

Setze die richtigen Kräfte ein:

Wenn man $\alpha \backslash alpha$ vergrößert, wird die ____________ größer und die __________ kleiner.

Die _________ bleibt konstant.

Die Formel für die Gewichtskraft kennst du schon: $F_G=m\cdot gF\_G=m\backslash cdot\; g$

Wir suchen nun eine Formel für die zwei neuen Kräfte. Dabei hilft uns das kleine rechtwinklige Dreieck rechts in der Abbildung. Wenn uns nur die Seitenlängen des Dreiecks interessieren, lassen wir die Vektorpfeile über den Kräften weg.

$\sin \alpha =\frac{Gegenkathete}{Hypotenuse}=\frac{F_H}{F_G}\backslash sin\backslash alpha=\backslash frac\{Gegenkathete\}\{Hypotenuse\}\; =\; \backslash frac\{F\_H\}\{F\_G\}$

liefert $F_H=F_G\cdot \sin \alpha =m\cdot g\cdot \sin \alpha F\_H=F\_G\; \backslash cdot\; \backslash sin\backslash alpha\; =\; m\; \backslash cdot\; g\; \backslash cdot\; \backslash sin\backslash alpha$

$\cos \alpha =\frac{Ankathete}{Hypotenuse}=\frac{F_N}{F_G}\backslash cos\backslash alpha=\backslash frac\{Ankathete\}\{Hypotenuse\}\; =\; \backslash frac\{F\_N\}\{F\_G\}$

liefert $F_N=F_G\cdot \cos \alpha =m\cdot g\cdot \cos \alpha F\_N=F\_G\; \backslash cdot\; \backslash cos\backslash alpha\; =\; m\; \backslash cdot\; g\; \backslash cdot\; \backslash cos\backslash alpha$

Da sich der Sinus und der Kosinus eines Winkels immer zwischen -1 und 1 bewegt, sind Hangabtriebskraft und Normalkraft immer kleiner als oder gleich groß wie die Gewichtskraft.

Du kennst schon die Formeln für die Geschwindigkeit und den zurückgelegten Weg bei einer Beschleunigung mit konstanter Kraft:

$v=a\cdot tv=a\backslash cdot\; t$

und

$s=\frac{1}{2}a{t}^{2}s=\backslash frac\{1\}\{2\}at^2$ $(2)(2)$

Würde das Brett senkrecht stehen ($\alpha =90\mathrm{°}\backslash alpha=90°$), wäre der Körper im Freien Fall und für die Geschwindigkeit und den zurückgelegten Weg gilt mit $a=ga=g$ (Erdbeschleunigung bzw. Ortsfaktor)

$v=g\cdot tv=g\; \backslash cdot\; t$

und

$s=\frac{1}{2}g{t}^{2}s=\; \backslash frac\{1\}\{2\}\; g\; t^2$

Bei der Schiefen Ebene wird nicht mit der ganzen Gewichtskraft beschleunigt, sondern nur mit einem Anteil, nämlich der Hangabtriebskraft. Also ist auch die Beschleunigung nur ein Anteil der Erdbeschleunigung. Die Kraft ist proportional zur Beschleunigung.

$F_H=m\cdot aF\_H=m\; \backslash cdot\; a$

$F_G\cdot \sin \alpha =m\cdot aF\_G\; \backslash cdot\; \backslash sin\backslash alpha\; =\; m\; \backslash cdot\; a$

$m\cdot g\cdot \sin \alpha =m\cdot am\; \backslash cdot\; g\; \backslash cdot\; \backslash sin\backslash alpha\; =\; m\; \backslash cdot\; a$ |$:m:m$

$g\cdot \sin \alpha =ag\; \backslash cdot\; \backslash sin\backslash alpha\; =\; a$

Nun wird es Zeit, dass wir das experimentell überprüfen. Baue dir dazu eine Schiefe Ebene und besorge dir ein Smartphone oder eine Digitaluhr zum Stoppen der Zeit. Als beschleunigter Körper kann dir eine Kugel, eine zylinderförmige Dose oder ein Spielzeugauto dienen. Mit einem Meterstab kannst du die Längen messen.

Die besten Werte bekommst du für kleine Neigungswinkel (z.B. 10°), dann kannst du nämlich die Zeit genauer messen.

Vorgehen:

1.) Über die „Fallzeit“ bestimmen wir die Beschleunigung.

2.) Aus den Abmessungen $ll$ und $hh$ berechnen wir den Neigungswinkel $\alpha \backslash alpha$ und damit den theoretischen Wert für die Beschleunigung.

3.) Dann vergleichen wir die beiden Werte.

zu 1.) Stoppe und notiere dir 10 Mal die Zeit, die dein Körper benötigt, um die ganze Länge $ll$ des Bretts abzufahren, von ganz oben nach ganz unten. Berechne den Mittelwert. Wir nennen ihn $t_{0}t\_0$.

Aus der Fall „Fallzeit“ $t_{0}t\_0$ ergibt sich für die Beschleunigung nach Gleichung $(2)(2)$

$a=\frac{2s}{t^2}=\frac{2l}{(t_0{)}^2}a=\backslash frac\{2s\}\{t^2\}\; =\; \backslash frac\{2l\}\{(t\_0)^2\}$

Setze deine Werte für $ll$ und $t_{0}t\_0$ ein.

Wir kontrollieren die Einheiten: Ja, links und rechts stehen $\frac{m}{s^2}\backslash frac\{m\}\{s^2\}$

zu 2.) Jetzt misst du $ll$ und $hh$ und rechnest sie in Meter um. Mit Gleichung (1) ergibt sich für den Neigungswinkel aus den Abmessungen

$\sin (\alpha )=\frac{h}{l}\backslash sin(\backslash alpha)=\backslash frac\{h\}\{l\}$

und somit

$\alpha ={\sin }^{-1}(\frac{h}{l})\backslash alpha=\backslash sin^\{-1\}(\backslash frac\{h\}\{l\})$

Kontrolliere, dass dein Taschenrechner auf DEG (Winkel im Gradmaß) steht, nicht auf RAD (Bogenmaß).

Wenn wir diesen Wert für $\alpha \backslash alpha$ in Gleichung $(3)(3)$ einsetzen, ergibt sich

$a=g\cdot \sin \alpha =\mathrm{9,81}\frac{m}{s^2}\cdot \sin \alpha a\; =\backslash \; g\; \backslash cdot\; \backslash sin\backslash alpha\; =\; 9\{,\}81\; \backslash frac\{m\}\{s^2\}\; \backslash cdot\; \backslash sin\backslash alpha$

zu 3.) Notiere dir:

aus den Zeitmessungen: $a=a\; =$ _________ $\frac{m}{s^2}\backslash frac\{m\}\{s^2\}$

aus den Abmessungen: $a=a\; =$ _________ $\frac{m}{s^2}\backslash frac\{m\}\{s^2\}$

Wenn du gut gemessen und richtig gerechnet hast, sollten sich die beiden Werte kaum unterscheiden.

Woran könnte der Unterschied liegen?

• Die Reibung ist in der Realität natürlich doch nicht zu vernachlässigen. Es tritt Reibung zwischen Körper und Brett und die Luftreibung auf.

• An dem Körper dreht sich wahrscheinlich etwas, wenn er nach unten rollt: Räder, die Kugel oder die Dose selbst. In dieser Rotation steckt auch Energie, die zur Beschleunigung fehlt.