Addition von Brüchen

Kurs

1 Das große Schlemmen

Moritz feiert seinen 12. Geburtstag mit seinen Freunden. Wie bei jeder guten Geburtstagsfeier gibt es reichlich Kuchen. Es gibt

einen Marmorkuchen und
einen Zitronenkuchen.

Am Ende der Party gehen Moritz Freunde und zurück bleiben einige Kuchenreste.

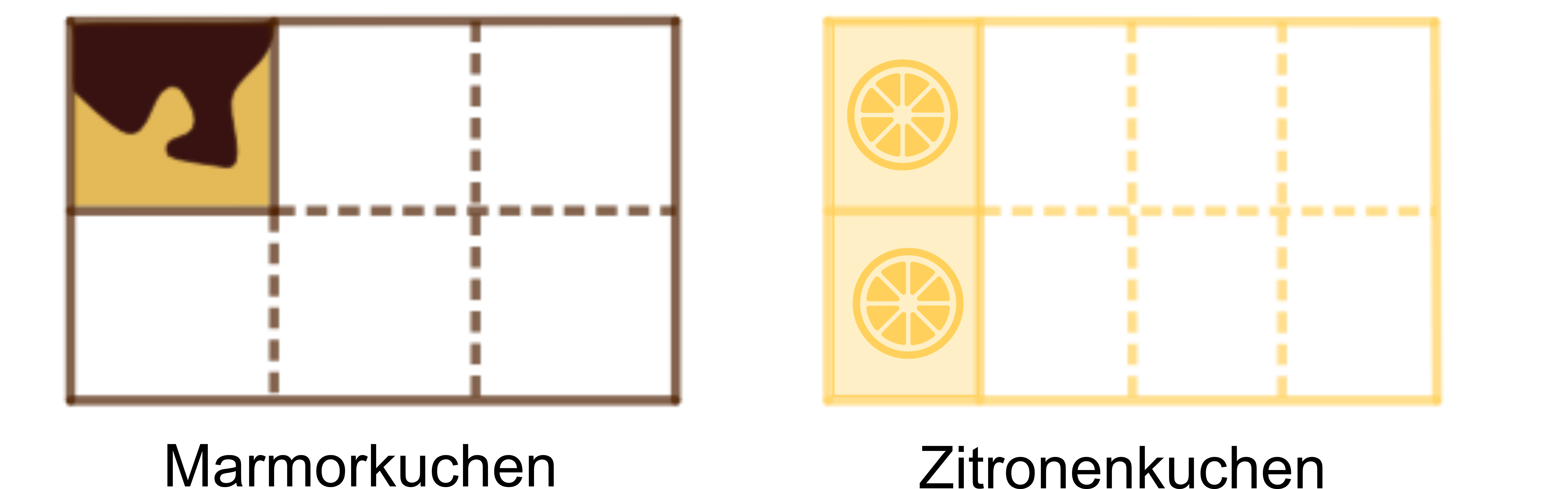
Er schiebt die restlichen Kuchenstücke zusammen. Wie viel Bleche Kuchen blieben am Ende der Party über?

Um die Lösung zu erfahren, klicke dich weiter ;)

2 Addition von gleichnamigen Brüchen

Um herauszufinden, wie viel Bleche Kuchen noch übrig sind, musst du Brüche addieren.

Gleichnamige Brüche

Um Brüche zu addieren, müssen diese den gleichen Nenner haben. Wenn wir uns den Zitronenkuchen beispielsweise ansehen, liegen dort 2 Stücke. Da der Kuchen in 8 gleich große Teile geschnitten wurde, ist jedes Stück $\frac{1}{8}$ Blech groß.

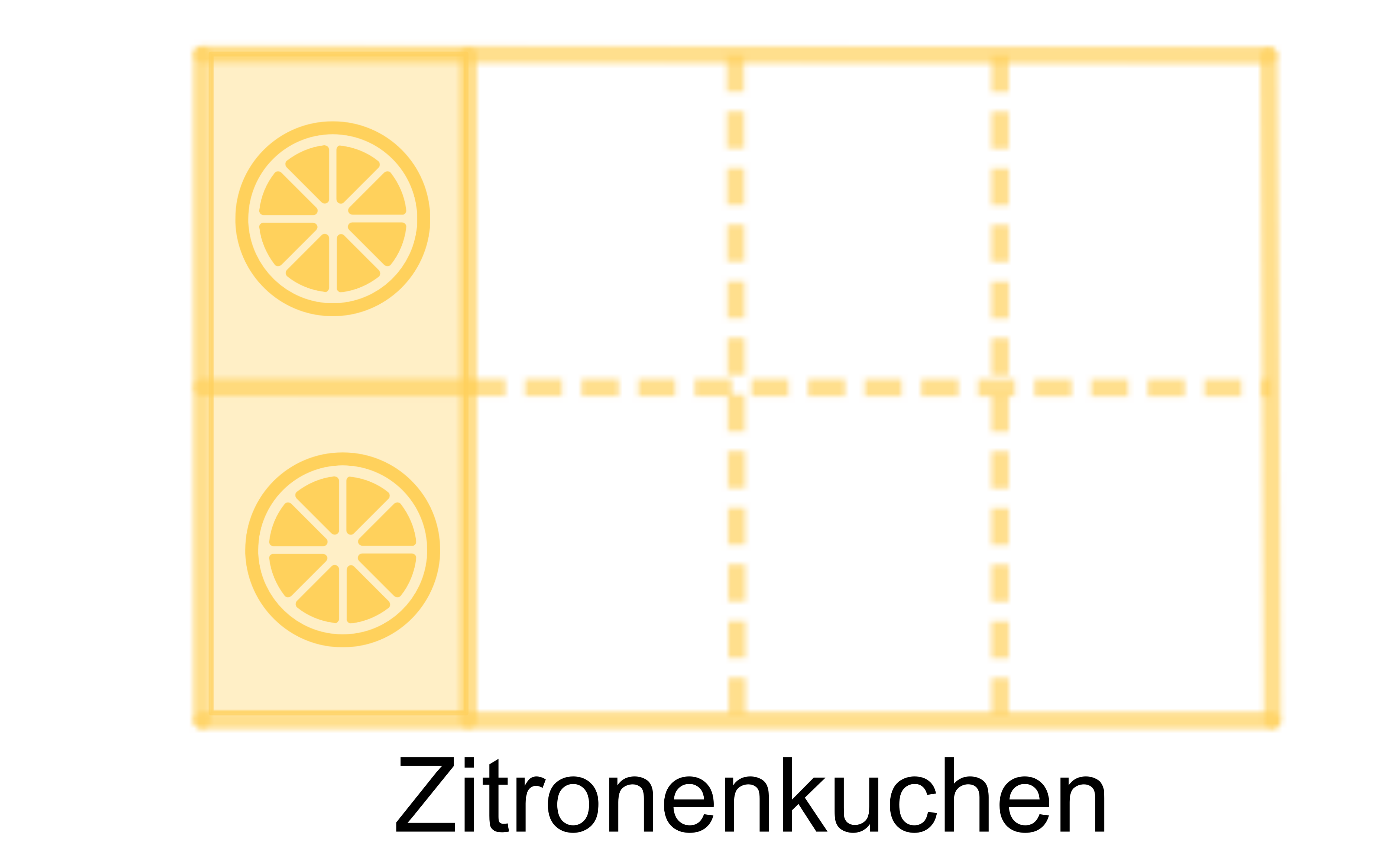
Insgesamt sind also $\frac{1}{8} + \frac{1}{8}$ Bleche Zitronenkuchen noch da. Diese sind zusammen $\frac{2}{8}$ Bleche groß,

\frac{1}{8} + \frac{1}{8} = \frac{1 + 1}{8} = \frac{2}{8}

Um gleichnamige Brüche zu addieren, addiert man die Zähler der Brüche. Der Nenner bleibt gleich.

Beispiel: $\frac{2}{5} + \frac{1}{5} = \frac{2 + 1}{5} = \frac{3}{5}$

3 Addition von ungleichnamigen Brüchen (1/2)

Ungleichnamige Brüche

Brüche mit unterschiedlichen Nennern müssen erst auf einen gemeinsamen Nenner gebracht werden. Dafür muss der Bruch auf ein gemeinsames Vielfaches der Nenner erweitert werden.

In unserem Beispiel:

Es bleiben $\frac{1}{6}$ Bleche Marmorkuchen und $\frac{2}{8}$ Bleche Zitronenkuchen übrig. Insgesamt sind es also $\frac{1}{6} + \frac{2}{8}$ Bleche.

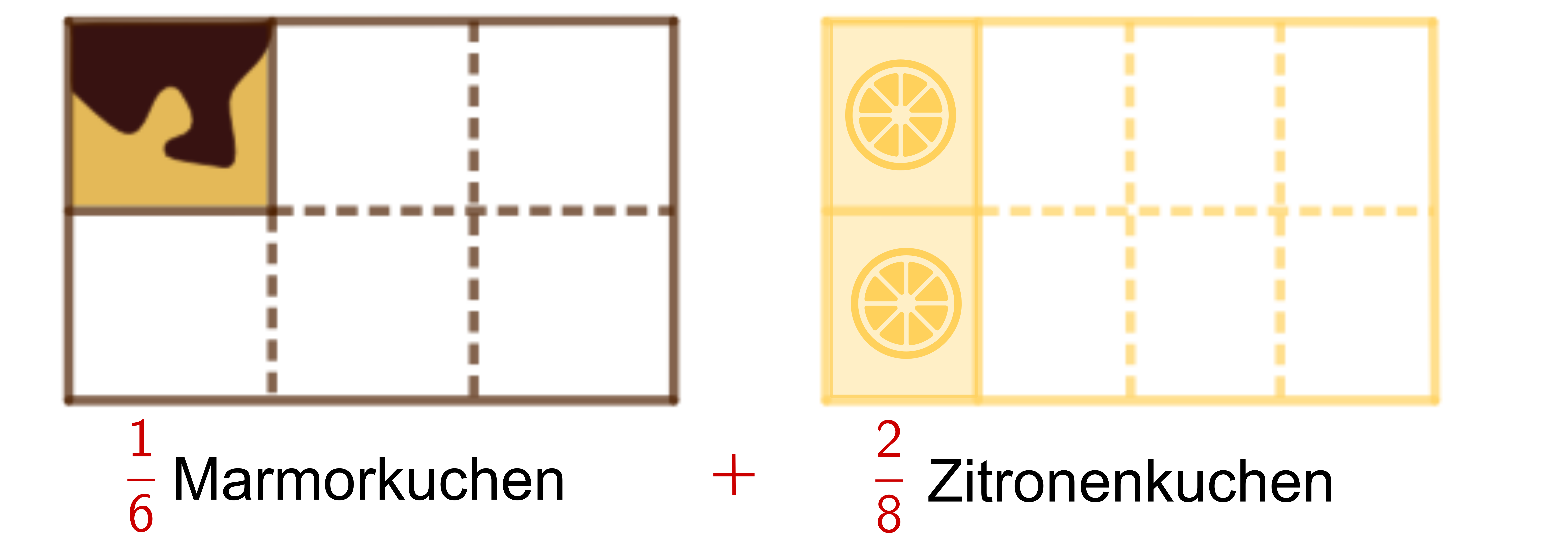
Wir teilen die Kuchen in gleich große Stücke. Um das zu machen, brauchen wir ein gemeinsames Vielfaches der Nenner 6 und 8, also beispielsweise 24.

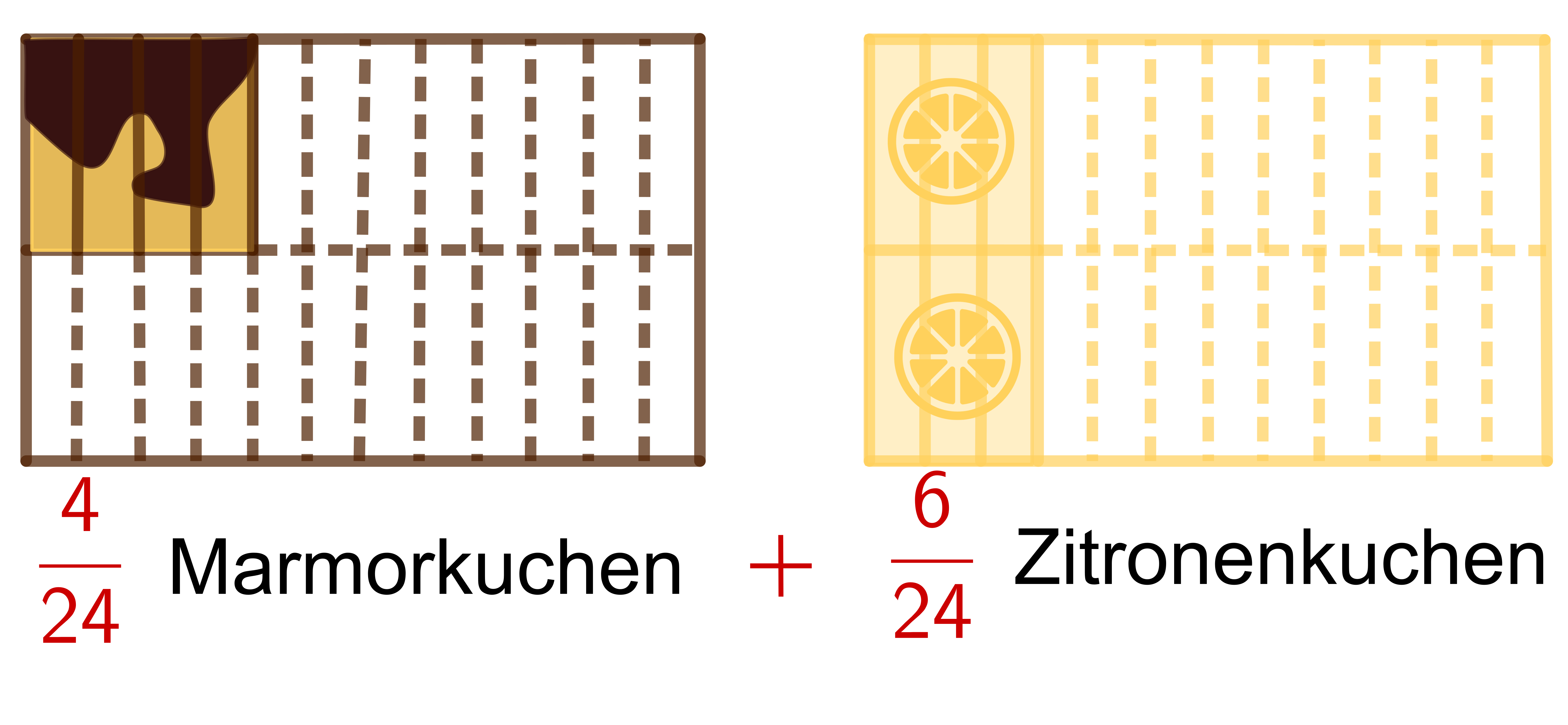
4 Addition von ungleichnamigen Brüchen (2/2)

Nun haben wir gleich große Kuchenstücke, die wir problemlos in ein Blech zusammensetzen und abzählen können.

Zusammenfassung

Um ungleichnamige Brüche zu addieren, müssen diese erst auf einen gemeinsamen Nenner gebracht werden.
Hierfür erweiterst du die Brüche auf ein gemeinsames Vielfaches der Nenner.
Danach kannst du die nun gleichnamigen Brüche addieren: Addiere die Zähler. Der Nenner bleibt unverändert.

Beispiel: $\frac{2}{3} + \frac{1}{4} = \frac{4 \cdot 2}{4 \cdot 3} + \frac{3 \cdot 1}{3 \cdot 4} = \frac{8}{12} + \frac{3}{12} = \frac{11}{12}$

5 Teste dein Wissen

Brüche lassen sich nur addieren, wenn sie den gleichen [Nenner] besitzen. Man addiert sie, indem man die Zähler [addiert]. Die Nenner werden [nicht verändert].

Wenn Brüche nicht [gleichnamig] sind, müssen diese erst [erweitert] werden auf [ein gemeinsames Vielfaches] der Nenner. Danach erst lassen sich die Brüche addieren.

[\Zähler] [\kürzen] [\gleichzählig] [\einen gemeinsamen Teiler]

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?