Grundlagen der Vektorrechnung 1

Kurs

1 Übersicht

Ziele des Kurses

Dieser Kurs soll eine Einführung des Vektorbegriffs liefern.

Dazu wird zunächst erklärt:

Was ist ein Vektor und wie wird er dargestellt?
Welche besonderen Vektoren gibt es?
Wie berechnet man den Vektor zwischen zwei Punkten?
Wie wird die Länge eines Vektors berechnet?

Beispielaufgaben vertiefen das Ganze.

Voraussetzungen

Um Unklarheiten zu vermeiden, sollte man sich bereits mit folgenden Themen gut auskennen:

Grundrechenarten
Grundlagen der Geometrie
2D- und 3D-Koordinatensystem

2 Was ist ein Vektor?

Verschiebungen in der Ebene oder im Raum sind durch einen ihrer Verschiebungspfeile eindeutig bestimmt. Die Menge aller Verschiebungspfeile, die gleich lang sind, parallel zueinander verlaufen und in die gleiche Richtung zeigen, stellen einen Vektor dar. Ein einzelner Pfeil aus der Menge der Verschiebungspfeile ist ein Repräsentant des Vektors.

Der Vektor $\vec{a}$ beschreibt die Verschiebung, die den Punkt $A$ in $A^{'}$ , $B$ in $B^{'}$ usw. verschiebt.

$\vec{a} = \vec{A A^{'}} = \vec{B B^{'}} = . . .$

Der Vektor $\vec{a}$ kann durch beliebig viele Repräsentanten dargestellt werden, die alle untereinander parallelgleich sind.

3 Darstellung von Vektoren

In der Schule werden schwerpunktmäßig Vektoren aus dem zweidimensionalen und dreidimensionalen Raum betrachtet.

Im $ℝ^{2}$ :

Algebraische Darstellung:

Kartesische Koordinaten

$\vec{a} = (\begin{array}{c} a_{1} \\ a_{2} \end{array})$

Dargestellt ist der Vektor $\vec{a} = (\begin{array}{c} 5 \\ - 1 \end{array})$ .

Im $ℝ^{3}$ :

Die zeichnerische Darstellung der Vektoren erfolgt wieder durch Pfeile.

Algebraische Darstellung:

Kartesische Koordinaten

$\vec{a} = (\begin{array}{c} a_{1} \\ a_{2} \\ a_{3} \end{array})$

Dargestellt ist der Vektor $\vec{a} = (\begin{array}{c} 3 \\ 4 \\ 5 \end{array})$ .

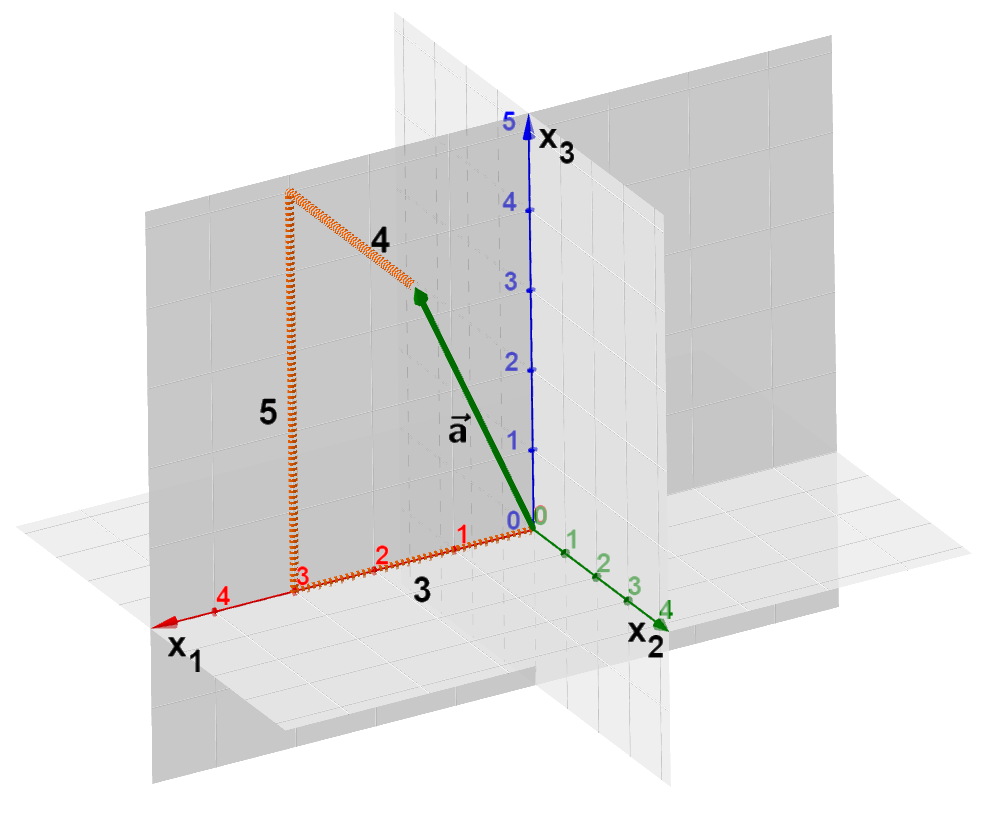
4 Besondere Vektoren

Der Nullvektor

Der Nullvektor in der Ebene ist $\vec{o} = (\begin{array}{c} 0 \\ 0 \end{array})$ .

Im Raum ist der Nullvektor $\vec{o} = (\begin{array}{c} 0 \\ 0 \\ 0 \end{array})$ .

Der Nullvektor hat keine Länge und damit auch keine Richtung. Er ist nicht als Pfeil darstellbar. Der Nullvektor wird aber für Rechenoperationen mit Vektoren benötigt.

Der Gegenvektor

Zu jedem Vektor $\vec{a}$ der Ebene bzw. des Raumes gibt es einen Vektor $- \vec{a}$ .

Der Vektor $- \vec{a}$ stimmt mit dem Vektor $\vec{a}$ in Länge und Richtung überein, weist jedoch eine entgegengesetzte Orientierung auf.

Der Vektor $- \vec{a}$ ist der Gegenvektor zum Vektor $\vec{a}$ .

Zum Vektor $\vec{a} = (\begin{array}{c} a_{1} \\ a_{2} \\ a_{3} \end{array})$ im Raum ist der Vektor $- \vec{a} = - (\begin{array}{c} a_{1} \\ a_{2} \\ a_{3} \end{array}) = (\begin{array}{c} - a_{1} \\ - a_{2} \\ - a_{3} \end{array})$ der Gegenvektor.

5 Vektor zwischen zwei Punkten berechnen

Vektoren sind oft dadurch gegeben, dass die Koordinaten zweier Punkte (z.B. $A$ und $B$ genannt) angegeben werden, zwischen denen ein Repräsentant des Vektors $\vec{v}$ verläuft.

In diesem Fall bezeichnet man den Vektor $\vec{v}$ auch mit $\vec{A B}$ .

Zeigt $\vec{v}$ vom Punkt $A$ zum Punkt $B$ , so heißt $A$ Fuß oder Fußpunkt und $B$ Spitze des Vektors $\vec{v}$ .

Möchte man nun die Koordinaten des Vektors $\vec{v}$ berechnen, der von $A (a_{1} | a_{2})$ nach $B (b_{1} | b_{2})$ zeigt, geht man wie folgt vor:

Man hält sich an den Merksatz:

"Spitze minus Fuß"

Man erhält die $x_{1} $ -Koordinate von $\vec{v}$ , indem man $a_{1} $ von b $_{1}$ abzieht. Entsprechend erhält man die $x_{2}$ -Koordinate, indem man $a_{2}$ von $b_{2}$ abzieht. Man erhält also:

\vec{v} = \vec{A B} = (\begin{array}{c} b_{1} - a_{1} \\ b_{2} - a_{2} \end{array})

Beispiel

Berechne den Verbindungsvektor $\vec{P Q}$ der Punkte $P (1; 3)$ und $Q (3; 2)$ .

Man hält sich an den Merksatz "Spitze minus Fuß", d.h. der Verbindungsvektor $\vec{P Q}$ wird als Differenzvektor berechnet.

$\vec{P Q} = \vec{Q} - \vec{P} = (\begin{array}{c} 3 \\ 2 \end{array}) - (\begin{array}{c} 1 \\ 3 \end{array}) = (\begin{array}{c} 2 \\ - 1 \end{array})$

6 Länge eines Vektors

Unter der Länge eines Vektors $\vec{a}$ versteht man die Länge der Pfeile, die den Vektor in einem Koordinatensystem darstellen. Statt Länge des Vektors $\vec{a}$ sagt man auch Betrag des Vektors $\vec{a}$ .

Jedem Vektor in der Ebene wird eine nicht negative reelle Zahl $| \vec{a} |$ zugeordnet, die Betrag des Vektors $\vec{a}$ heißt.

$\vec{a} = (\begin{array}{c} a_{1} \\ a_{2} \end{array}) \Rightarrow | \vec{a} | = \sqrt{a_{1}^{2} + a_{2}^{2}}$

Im Raum gilt entsprechend:

$\vec{a} = (\begin{array}{c} a_{1} \\ a_{2} \\ a_{3} \end{array}) \Rightarrow | \vec{a} | = \sqrt{a_{1}^{2} + a_{2}^{2} + a_{3}^{2}}$

Der Vektor $\vec{a} = (\begin{array}{c} 4 \\ 3 \end{array})$ in der Abbildung hat die Länge $5$ (das ist sein Betrag):

| \vec{a} | = \sqrt{4^{2} + 3^{2}} = \sqrt{16 + 9} = \sqrt{25} = 5

7 Übungsaufgaben

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

1 Übersicht

Ziele des Kurses

Voraussetzungen

2 Was ist ein Vektor?

3 Darstellung von Vektoren

Im ℝ2:

Algebraische Darstellung:

Im ℝ3:

Algebraische Darstellung:

4 Besondere Vektoren

Der Nullvektor

Der Gegenvektor

5 Vektor zwischen zwei Punkten berechnen

Beispiel

6 Länge eines Vektors

7 Übungsaufgaben

Im $ℝ^{2}$ :

Im $ℝ^{3}$ :