Das Potenzieren ist eine verkürzte Schreibweise für das mehrmalige Multiplizieren einer Zahl mit sich selbst.
Beispiel: Man schreibt als .
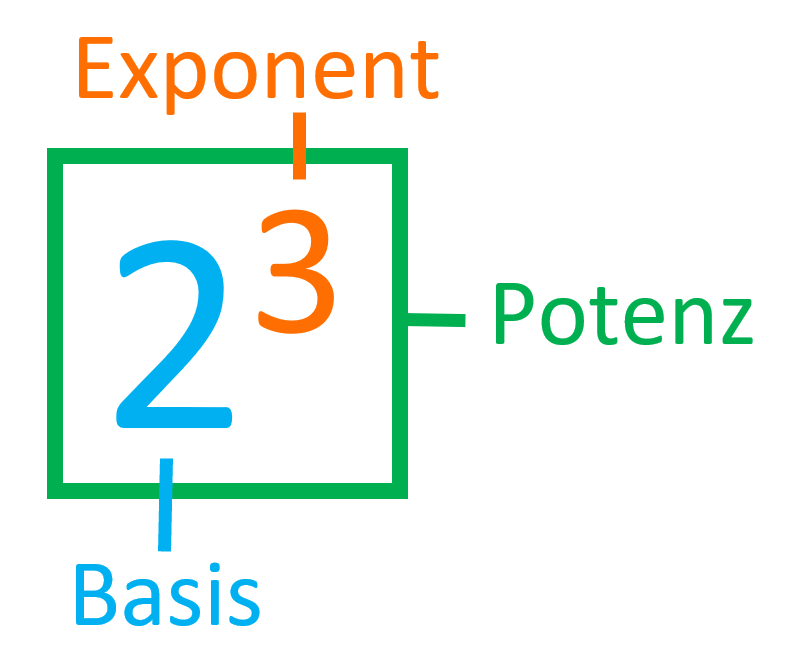
Der Exponent bzw. die Hochzahl, in diesem Beispiel die 3, beschreibt, wie oft eine Zahl mit sich selbst multipliziert wird.
Generell hat jede Zahl ohne Exponenten den Exponent .
Es gilt: .
Der Exponent wird in diesem Fall meist weggelassen.
Beispiel:
Potenziert man eine beliebige Zahl mit , so erhält man immer .
Beispieltabelle
1 | 2 | 3 | 4 | 5 | |
|---|---|---|---|---|---|
Basis und Exponent
Die Zahl, welche mit sich selbst multipliziert werden soll, nennt man Basis, die Anzahl Exponent, beides zusammen ist die Potenz und das Ergebnis dieser Rechnung ist der Wert der Potenz.

Potenzen mit negativer Basis
Wird eine negative Zahl potenziert, hängt das Vorzeichen des Ergebnisses davon ab, ob der Exponent eine gerade oder ungerade Zahl ist. Ist er gerade, ist das Ergebnis positiv, ist er ungerade, bleibt die Potenz negativ.
Beispiel:
Rechnen wir aus:
Der Term ist positiv, weil die Zahl größer als Null ist. Beim Term können wir verwenden, dass „Minus mal Minus Plus ergibt“. Es ist:
Man sieht:
Wenn also eine gerade Zahl ist, ist positiv und wenn eine ungerade Zahl ist, ist negativ. Somit ist auch positiv, wenn gerade ist, und negativ, wenn ungerade ist.
Potenzen mit negativem Exponenten
Wie kann man interpretieren?
In der nebenstehenden Grafik kann man folgendes sehen: Wenn der Exponent um eins kleiner wird, muss man das Ergebnis durch die Basis teilen. Das kennst du schon bei positiven Exponenten und kannst das auch bei negativen Exponenten weitermachen.
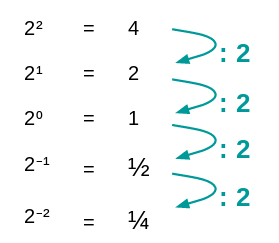
Hier siehst du das Ganze nochmal allgemein für . Am Ende steht dann die allgemeine Formel von oben.

Beispiele:
Rationale Exponenten
Zahlen, die man mit einer rationalen Zahl (also einem Bruch) potenziert, kann man als Wurzel identifizieren:
Damit gilt umgekehrt für die Standard-Wurzel:
Beispiele:
Rechnen mit Potenzen
Im Artikel Potenzgesetze kannst du nachlesen, wie man mit Potenzen rechnet und welche Potenzgesetze es gibt.
Übungsaufgaben
Laden
Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:
Aufgaben zu einfachen Potenzen
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
