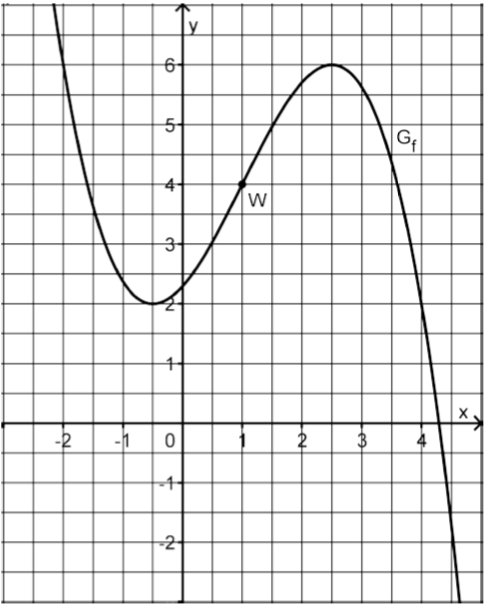
In dieser Aufgabe soll eine durch ihren Graphen gegebene Funktion graphisch differenziert werden, indem wesentliche Zusammenhänge zwischen den Graphen von Funktion und Ableitungsfunktion erfasst und abgelesen werden.

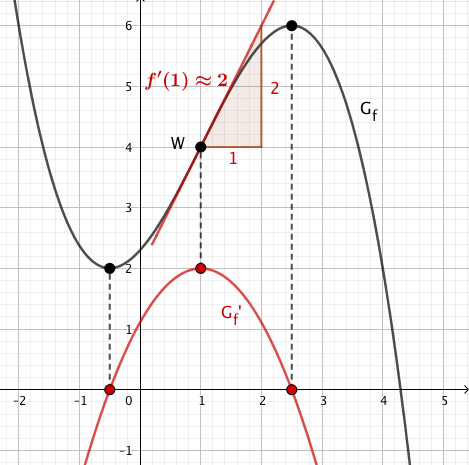
Die Ableitungsfunktion ist die Steigung an einem bestimmten Punkt, also kann ein Steigungsdreieck im Punkt $WW$ mit den Seitenlängen $1LE1\backslash ,\; LE$ und $2LE2\; \backslash ,LE$ als brauchbare Näherungslösung für die Berechnung des Steigungswertes, und damit als Wert für die Ableitung, in W genommen werden.

Damit gilt: $f^{\mathrm{\prime }}(1)\approx 2f\text{'}(1)\backslash approx2$.

Zur Skizze des Graphen $G_{f^{\mathrm{\prime }}}G\_\{f\text{'}\}$ kann man die folgenden Überlegungen anstellen:

Lokale Extrema sind Nullstellen der Ableitung. Also gibt es zwei Nullstellen $(-0,5\mathrm{\mid }0)(-0\{,\}5|0)$ und $(2,5\mathrm{\mid }0)(2\{,\}5|0)$. Wendepunkte sind Extrema in der Ableitung. Der Wendepunkt des Graphen ist ca. bei $x=1x=1$ und für diesen Wert weiß man die ungefähre Steigung $m=2m=2$, also liegt das Extremum der Ableitungsfunktion bei $(1\mathrm{\mid }2)(1|2)$. Abschließend überlegt man sich, in welchen der Bereiche der Graph steigt oder fällt. Für positive Steigung ist die Ableitungsfunktion positiv, für fallende Steigung negativ. Es ergibt sich daher eine nach unten geöffnete Parabel.

Ergänzende Begründung

$G_{f}G\_f$ besitzt zwei lokale Extrema und ist offensichtlich punktsymmetrisch zum Wendepunkt $WW$. Die zugehörige Funktion $ff$ könnte somit mit hoher Genauigkeit eine ganzrationale Funktion 3. Grades sein. Die gesuchte Ableitungsfunktion $f^{\mathrm{\prime }}f\text{'}$ somit zumindest näherungsweise eine ganzrationale Funktion 2. Grades. Der Graph dann tatsächlich eine Parabel.

Der Scheitelpunkt der Parabel hat dann die Koordinaten $(1\mathrm{\mid }{f}^{\mathrm{\prime }}(1))\approx (1\mathrm{\mid }2)(1|f\text{'}(1))\backslash approx(1|2)$. Die Nullstellen der nach unten geöffneten Parabel sind die x-Werte der lokalen Extrema von $ff$, also die Werte $-0,5-0\{,\}5$ und $2,52\{,\}5$.