Analysis, Teil A, Aufgabengruppe 1

🎓 Prüfungsbereich für Bayern

Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

Die Aufgabenstellung findest du hier zum Ausdrucken als PDF.

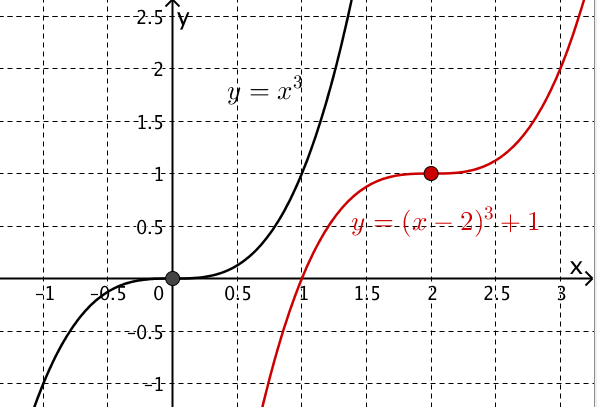
Geben Sie für die Funktionen f $_1$ und f $_2$ jeweils die maximale Definitionsmenge und die Nullstelle an.

$\displaystyle\quad f_1:x \mapsto \frac{2x+3}{x^2-4}$ $\quad\quad f_2:x\mapsto\ln(x+2)$

(4 BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Gebrochenrationale Funktionen

In der Aufgabe ist eine gebrochenrationale Funktion und eine natürliche Logarithmusfunktion gegeben. Es ist ihre maximal mögliche Definitionsmenge zu bestimmen, sowie ihre Nullstellen zu berechnen.

Maximale Definitionsmenge der Funktion $f_1$

$f_1$ ist eine gebrochen rationale Funktion. Ihre maximale Definitionsmenge $\mathrm{D}_\text{max}(f_1)$ ist die Menge der reellen Zahlen $\mathbb{R}$ außer den Nullstellen des Nenners.

Nullstellen des Nenners:

$\displaystyle x^2-4$	$=$	$\displaystyle 0$	$\displaystyle +4$
$\displaystyle x^2$	$=$	$\displaystyle 4$	$\displaystyle \sqrt{ }$
$\displaystyle x_{\frac{1}{2}}$	$=$	$\displaystyle \pm2$
$\displaystyle \Rightarrow\ D_{\max}\left(f_1\right)$	$=$	$\displaystyle \mathbb R\backslash\{-2;2\}$

Nullstelle(n) der Funktion $f_1$

$\displaystyle \frac{2x+3}{x^2-4}$	$=$	$\displaystyle 0$	$\displaystyle \cdot Nenner$
$\displaystyle 2x+3$	$=$	$\displaystyle 0\cdot\left(x^2-4\right)$
	↓	Beachte die 0!
$\displaystyle 2x+3$	$=$	$\displaystyle 0$	$\displaystyle -3\ :2$
$\displaystyle x$	$=$	$\displaystyle -1{,}5$

und es gilt: $-1{,}5$ $\in D_{\max}(f_1)$

Die Funktion $f_1$ hat also die Nullstelle (-1,5|0).

Maximale Definitionsmenge der Funktion $f_2$

$f_2$ hat als ln-Funktion als maximale Definitionsmenge die Menge aller reeller Zahlen, für die $x+2$ positiv ist.

Also gilt die Bedingung:

$\displaystyle x+2$	$>$	$\displaystyle 0$
$\displaystyle x$	$>$	$\displaystyle -2$
$\displaystyle \Rightarrow\ D_{\max}\left(f_2\right)$	$=$	$\displaystyle \left]-2;+\infty\right[$

Die Zahlenmenge des maximalen Definitionsbereichs von $f_2$ kann auch mit einer Doppelungleichung angegeben werden:

$\quad \quad \;\left\{ x\,|-2<x<+\infty\right\}$

Nullstelle(n) der Funktion $f_2$

$\displaystyle \ln\left(x+2\right)$	$=$	$\displaystyle 0$	$\displaystyle e^0$
$\displaystyle x+2$	$=$	$\displaystyle e^0$
$\displaystyle x+2$	$=$	$\displaystyle 1$
$\displaystyle x$	$=$	$\displaystyle -1$

und es gilt: $-1$ $\in\,D_{max}(f_2)$

Die Funktion $f_2$ hat also die Nullstelle (-1|0).

Hast du eine Frage oder Feedback?

Bitte melde dich an, um diese Funktion zu benutzen.

2
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Geben Sie den Term einer in $\mathbb{R}$ definierten Funktion an, deren Graph im Punkt $(2|1)$ eine waagrechte Tangente, aber keinen Extrempunkt hat.
(3 BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Terrassenpunkte
Für die Funktion $f_0: y = x^3;\;\mathbb{D}= \mathbb{R}$ ist der Koordinatenursprung $(0|0)$ Terrassenpunkt.
Die Verschiebung des Graphen von $f_0$ um 2 LE nach rechts und 1 LE nach oben erzeugt eine der gesuchten Funktionen:
$f:y =(x-2)^3+1;\;\mathbb{D}=\mathbb{R}$
Alternative Lösung
Kennst du keine Funktion mit einem Terrassenpunkt, dann überlegst du so:
Damit der Punkt $(2|1)$ Terrassenpunkt einer zu bestimmenden Funktion $f$ wird, muss die 1. Ableitung $\;f'$ für $x=2$ eine doppelte Nullstelle (allgemeiner eine gerade Nullstelle) besitzen. Ansatz:
$(2|1)$ in $f$ eingesetzt ergibt:
Also ist $f(x)=\frac{1}{3}(x-2)^3+1$ eine zweite, auf anderem Wege gefundene Lösung der Aufgabe.
Weitere Lösungen wären z.B. über folgende Ansätze für $f'$ möglich:
$f'(x)=a\cdot(x-2)^2,\; a\neq0$ oder auch $f'(x)=(x+1)(x-2)^2$
In einem vorgegebenen Punkt sind beliebig viele Funktionen denkbar, für die dieser Terrassenpunkt ist.
Eine naheliegende Lösungsstrategie ist die Betrachtung einer bekannten Funktion mit beliebigem Terrassenpunkt und anschließende Verschiebung dieses Punktes in den Punkt $(2|1)$ .
3
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Gegeben ist die in $\mathbb{R}$ definierte Funktion $f$ mit $f(x)=-x^3+9x^2-15x-25$ .
Weisen Sie nach, dass $f$ folgende Eigenschaften besitzt:
(1) Der Graph von $f$ besitzt an der Stelle x =0 die Steigung -15.
(2) Der Graph von $f$ besitzt im Punkt $A(5|f(5))$ die x-Achse als Tangente.
(3) Die Tangente $t$ an den Graphen der Funktion $f$ im Punkt $B(-1|f(-1))$ kann durch die Gleichung $y=-36x-36$ beschrieben werden.
(5 BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Tangente an Graph
(1)
Berechne mit der 1. Ableitung von $f$ den Steigungswert für $x=0$ .
(2)
Berechne zunächst die 2. Koordinate des Punktes $A$
Damit ist $A$ eine Nullstelle und die x-Achse Tangente, wenn $f'(5)=0$ .
Alternative Überlegung:
Eine Nullstelle hat die x-Achse als Tangente, wenn es sich um eine doppelte Nullstelle handelt.
Nachweis, dass $x=5$ eine doppelte Nullstelle von $f$ ist, durch die Polynomdivision: $(-x^3+9x^2-15x-25):(x-5)^2$
Damit gilt:
Somit ist $x=5$ eine doppelte Nullstelle von $f$ und die Tangente im Punkt $A$ ist die x-Achse.
(3)
Berechne zunächst die 2. Koordinate des Punktes $B$ :
Berechne die Steigung an dem Punkt:
Für die Geradengleichung der Tangente $t$ in $B$ gilt: $\\t:\displaystyle \frac{y-y_B}{x-x_B}=f'(x_B)\\ t:\displaystyle\frac{y-0}{x+1}=-36\quad|\cdot{(x+1)} \\ t:y=-36x-36$
4
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
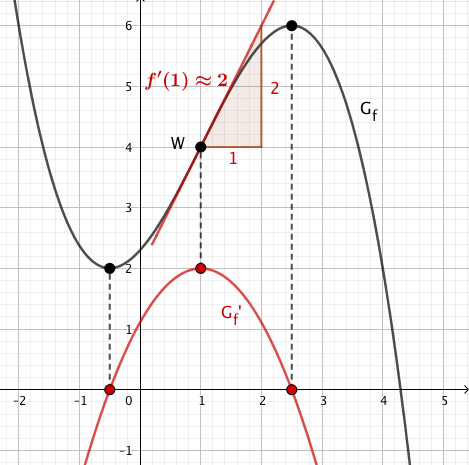
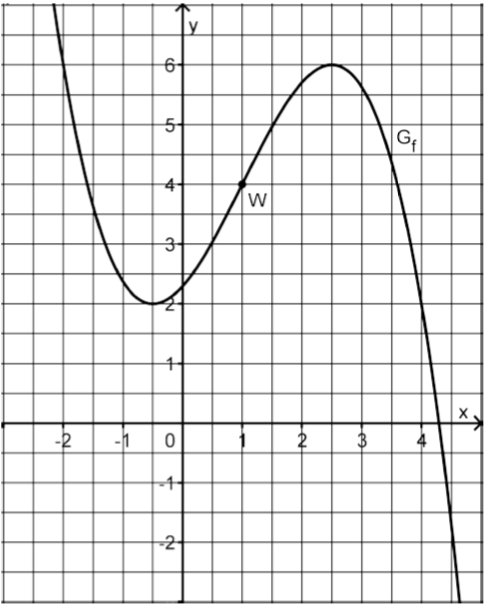
Die Abbildung zeigt den Graphen $G_f$ einer in $\mathbb{R}$ definierten Funktion $f$ mit dem Wendepunkt $W(1|4)$ .
Ermitteln Sie mit Hilfe der Abbildung näherungsweise den Wert der Ableitung von $f$ an der Stelle $x=1$ .
Skizzieren Sie den Graphen der Ableitungsfunktion $f'$ von $f$ in die Abbildung; berücksichtigen Sie dabei insbesondere die Lage der Nullstellen von $f'$ sowie den für $f'(1)$ ermittelten Näherungswert.
(3 BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Kurvendiskussion
In dieser Aufgabe soll eine durch ihren Graphen gegebene Funktion graphisch differenziert werden, indem wesentliche Zusammenhänge zwischen den Graphen von Funktion und Ableitungsfunktion erfasst und abgelesen werden.
Die Ableitungsfunktion ist die Steigung an einem bestimmten Punkt, also kann ein Steigungsdreieck im Punkt $W$ mit den Seitenlängen $1\, LE$ und $2 \,LE$ als brauchbare Näherungslösung für die Berechnung des Steigungswertes, und damit als Wert für die Ableitung, in W genommen werden.
Damit gilt: $f'(1)\approx2$ .
Zur Skizze des Graphen $G_{f'}$ kann man die folgenden Überlegungen anstellen:
Lokale Extrema sind Nullstellen der Ableitung. Also gibt es zwei Nullstellen $(-0{,}5|0)$ und $(2{,}5|0)$ . Wendepunkte sind Extrema in der Ableitung. Der Wendepunkt des Graphen ist ca. bei $x=1$ und für diesen Wert weiß man die ungefähre Steigung $m=2$ , also liegt das Extremum der Ableitungsfunktion bei $(1|2)$ . Abschließend überlegt man sich, in welchen der Bereiche der Graph steigt oder fällt. Für positive Steigung ist die Ableitungsfunktion positiv, für fallende Steigung negativ. Es ergibt sich daher eine nach unten geöffnete Parabel.
Ergänzende Begründung
$G_f$ besitzt zwei lokale Extrema und ist offensichtlich punktsymmetrisch zum Wendepunkt $W$ . Die zugehörige Funktion $f$ könnte somit mit hoher Genauigkeit eine ganzrationale Funktion 3. Grades sein. Die gesuchte Ableitungsfunktion $f'$ somit zumindest näherungsweise eine ganzrationale Funktion 2. Grades. Der Graph dann tatsächlich eine Parabel.
Der Scheitelpunkt der Parabel hat dann die Koordinaten $(1|f'(1))\approx(1|2)$ . Die Nullstellen der nach unten geöffneten Parabel sind die x-Werte der lokalen Extrema von $f$ , also die Werte $-0{,}5$ und $2{,}5$ .
5
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
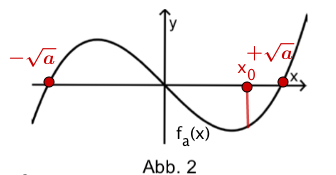
Für jeden Wert $a$ mit $a\in\mathbb{R^+}$ ist eine Funktion $f_a$ durch $f_a(x)=\frac1 a \cdot x^3-x$ mit $x\in\mathbb{R}$ gegeben.
a) Eine der beiden Abbildungen stellt einen Graphen von $f_a$ dar. Geben Sie an, für welche Abbildung dies zutrifft. Begründen Sie Ihre Antwort.(2 BE)
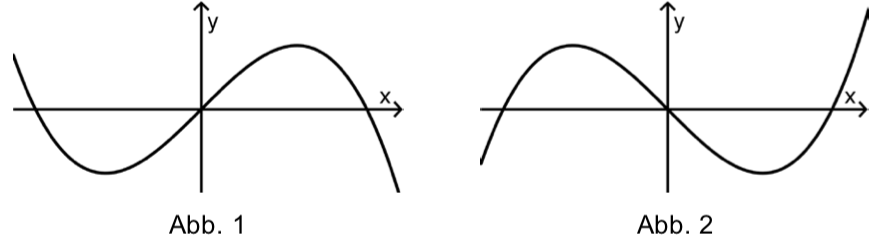
b) Für jeden Wert von $a$ besitzt der Graph von $f_a$ genau zwei Extrempunkte. Ermitteln Sie denjenigen Wert von $a$ , für den der Graph der Funktion $f_a$ an der Stelle $x=3$ einen Extrempunkt hat. (3 BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Funktionenschar
Teilaufgabe a)
Abbildung 2 zeigt einen Graphen aus der Funktionenschar $f_a$ .
Begründung:
Das Verhalten einer ganzrationalen Funktion für $x\rightarrow\pm\infty$ wird bestimmt durch das Vorzeichen des Faktors beim Glied mit dem höchsten Exponenten.
Da $a\in\mathbb{R^+}$ ist $\displaystyle\frac1 a>0$ und es gilt: $\lim\limits_{x\to +\infty} f_a(x)=+\infty$ .
Alternative Begründung ohne Grenzwertbetrachtung
$f_a(x)$ läßt sich in Linearfaktoren zerlegen:
$\displaystyle f_a(x)= \frac 1a x ^3 - x=\frac1a \cdot x \cdot (x^2-a)=\frac1a \cdot x \cdot (x-\sqrt{a})(x+\sqrt{a})$
Beachte die Benutzung der 2. binomischen Formel für $x^2-a=x^2- (\sqrt{a})^2$ .
Für alle Werte $x_0$ mit $0<x_0<\sqrt{a}$ gilt dann wegen der Vorzeichenreihe $\;+\;+\;-\;\;+$ der Linearfaktoren, dass $f_a(x_0)<0$ .
In Worten: "Plus mal plus mal minus mal plus ist minus".
Abbildung 2 ist also passend.
Teilaufgabe b)
Notwendige Bedingung, dass $x=3$ ein Extremum ergibt: $\quad f_{a}'(3)=0$
$\def\arraystretch{1.25} \begin{array} {lcll} &&&\text{Differenziere}\,f_{a}(x)\\ f_{a}'(x) &= &\displaystyle \frac{3}{a}x^2-1 &\text{Setze für}\; {\color{red}x}\;\text{den Wert 3 ein.}\\f_{a}'(3)&=&\displaystyle \frac{27}{a}-1&\text{Setze}\;\;f_{a}'(3)=0 \\\displaystyle \frac{27}{a}-1&=&0&|\cdot a\;\;\text{(Gleichung für a!)}\\27-a&=&0\\\quad \quad a&=&27\end{array}$
Nachweis, dass $a=27$ für $x=3$ tatsächlich ein lokales Extremum ergibt:
$\def\arraystretch{1.25} \begin{array} {lcll}& & & \text{Differenziere}\, f_{a}'(x) \\f_{a}''(x) &= &\displaystyle\frac{6}{a}\cdot x &\text {Setze}\;{\color{red}a}=27 \;\text{ein}\\f_{27}''(x)&=&\displaystyle \frac{6}{27} \cdot x&\text{Setze}\;x=3\\f_{27}''(3)& = &\frac{2}{3}\, > \,0&\Rightarrow\;\text{x = 3 ergibt für} \,f_{27}\, \text {ein lokales Minimum} \end{array}$