1 Kursübersicht
In diesem Kurs lernst du
was eine lineare Funktion ist
wie der Funktionsterm einer linearen Funktion aufgestellt wird
welche Parameter den Verlauf des Graphen bestimmen
Um diesen Kurs bearbeiten zu können, solltest du bereits folgendes können:
Berechnung von Proportionalitäten
Bestimmung der Steigung von Geraden durch Steigungsdreiecke
Erstellen einer Wertetabelle
Zeichnen eines Graphen anhand einer Wertetabelle
Der Kurs dauert ca. h.
2 Aufstieg zur Zugspitze
Jonathan, Bianca und Hannes waren in den Ferien mal wieder richtig fleißig und haben die Zugspitze bestiegen (mit knapp 3000 m der höchste Berg Deutschlands). Dabei steigen die drei in der gleichen konstanten Geschwindigkeit, nämlich 500 m pro Stunde, auf, aber sie starten von verschiedenen Ausgangspunkten.
Jonathan fährt mit dem Zug aus München und startet seinen Anstieg von Meereshöhe (0 m). Bianca hat auf einer Hütte am Eibsee übernachtet (dieser liegt auf einer Höhe von knapp 1000 m) und startet von dort. Hannes lässt es sich gut gehen, er fährt mit der Zahnradbahn bis auf 2500 m auf das Zugspitzplatt und schaut sich vorher den Gletscher an, bevor er Richtung Gipfel startet.
Das folgende Applet erklärt dir, wie sich der Aufstieg der drei mathematisch darstellen lässt.
Falls dir kein Applet angezeigt wird, kannst du es über diesen Link abrufen: Applet zum Aufstieg zur Zugspitze
3 Der y-Achsenabschnitt
Graphen wie den von Jonathans Aufstieg kennst du bereits. Bestimme seinen Funktionsterm!
Doch was ist mit den anderen Graphen? Diese verlaufen nicht durch den Ursprung. Kannst du trotzdem ihre Steigung bestimmen? Betrachte das nachfolgende Applet und erfahre, welche Gemeinsamkeiten und Unterschiede die Graphen und somit die Funktionsterme besitzen.
Falls dir kein Applet angezeigt wird, kannst du es über diesen Link abrufen: Applet zum Aufstieg zur Zugspitze
Laden
4 Lineare Funktionen
Die Formen dieser Funktionsgraphen hast du vielleicht schon einmal gesehen, aber jetzt kannst du diese mithilfe eines Funktionsterms darstellen.
und
Diese Art von Funktionen heißen lineare Funktionen.
Dies halten wir nun noch allgemein fest.
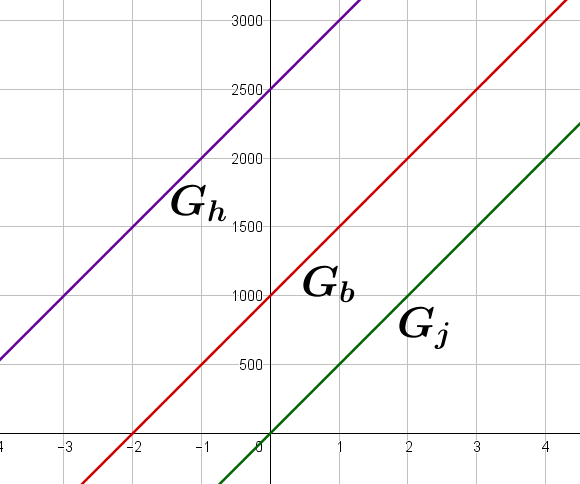
Eine Funktion heißt lineare Funktionen. Dabei ist die Steigung der Funktion und die Verschiebung des Graphen nach oben oder nach unten .
Mit berechnet man den Funktionswert an der Stelle . An der Stelle schneidet der Graph die Achse, daher nennt man auch den Achsenabschnitt.
Rechts siehst du weitere Beispiele für Graphen linearer Funktionen:
5 Übung
Laden
6 Zeichnen von linearen Funktionen
Um dir merken zu können, was lineare Funktionen sind, denk dir einfach: Lineare Funktionen sind Funktionen, die man mit einem Lineal zeichnen kann.
Aber wie zeichnet man nun den Graphen einer linearen Funktion, wenn nur der Funktionsterm gegeben ist?
Klar kannst du jedes Mal eine Wertetabelle anlegen, aber das ist auf Dauer etwas zeitaufwendig.
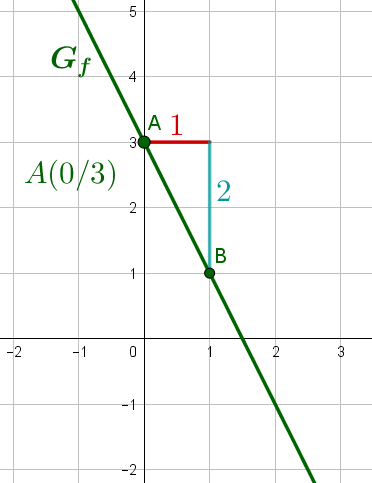
Angenommen, es sei die Funktion gegeben.
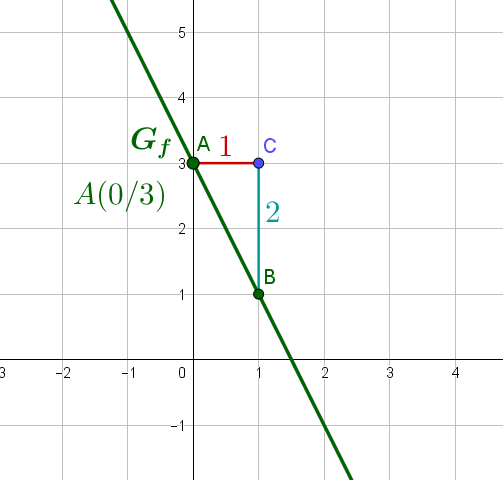
1. Steigungsdreieck
Wie du direkt aus dem Funktionsterm ablesen kannst, schneidet der Graph die Achse im Punkt , hier als bezeichnet.
Einen zweiten Punkt erhältst du mit Hilfe des Steigungsdreiecks. Da die Steigung hier beträgt, gehst du vom Punkt und und erhältst den Punkt .
Nun kannst du den Graphen durch die beiden Punkte zeichnen.
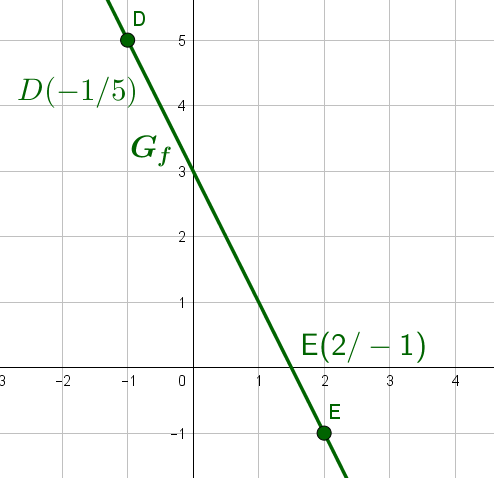
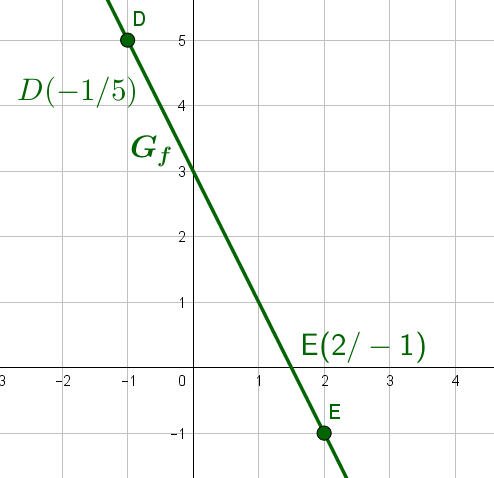
2. Funktionswerte
Man berechnet zwei beliebige unterschiedliche Funktionswerte und erhält auf diese Weise zwei Punkte, durch die die Gerade festgelegt ist.
Achte darauf, dass sowohl die Werte, als auch die Werte genaue Zahlenwerte ergeben, die du eindeutig einzeichnen kannst.
Zum Beispiel ist und .
Dadurch erhält man die Punkte und .
7 Zusammenfassung
Lass uns das Wichtigste noch einmal zusammenfassen.
Was sind lineare Funktionen?
Eine Funktion heißt lineare Funktionen. Dabei ist die Steigung der Funktion und die Verschiebung des Graphen nach oben oder nach unten .
Mit berechnet man den Funktionswert an der Stelle . An der Stelle schneidet der Graph die Achse, daher nennt man auch den Achsenabschnitt.
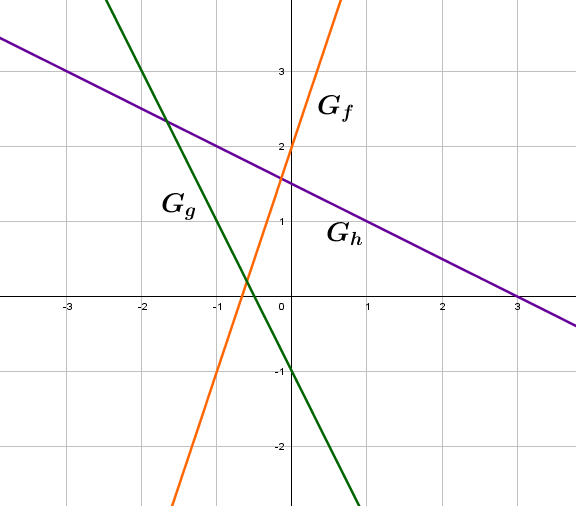
Graphen
Die Graphen linearer Funktionen sind Geraden.
Hier siehst du die Graphen der Funktionsterme und .
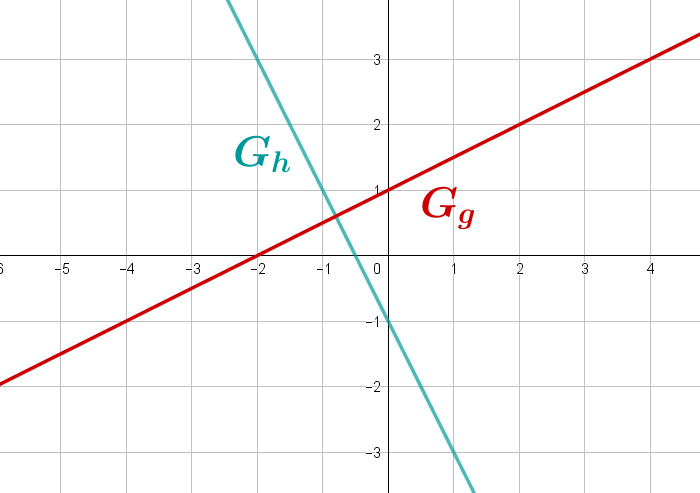
Zeichnen linearer Funktionen
Der Graph einer linearen Funktion ist durch zwei Punkte eindeutig festgelegt. Diese erhältst du entweder
(1) über den Achsenabschnitt und das Steigungsdreieck oder (2) über die Berechnung zweier unterschiedlicher Punkte.
Zum Beispiel:
1. Steigungsdreieck
2. Funktionswerte
8 Weiterführende Übungen
Laden
Laden
Laden
