Stochastik, Teil A, Aufgabengruppe 2

🎓 Prüfungsbereich für Bayern

Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

Die Aufgabenstellung findest du hier zum Ausdrucken als PDF.

1
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
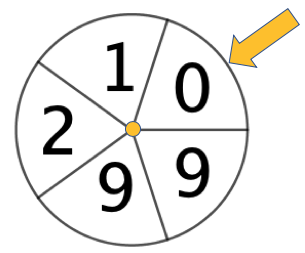
Ein Glücksrad besteht aus fünf gleich großen Sektoren. Einer der Sektoren ist mit "0" beschriftet, einer mit "1" und einer mit "2"; die beiden anderen Sektoren sind mit "9" beschriftet.
a)
(2 BE)
Das Glücksrad wird viermal gedreht. Berechnen Sie die wahrscheinlichkeit dafür, dass die Zahlen $2$ , $0$ , $1$ und $9$ in der angegebenen Reihenfolge erzielt werden.
b)
(3 BE)
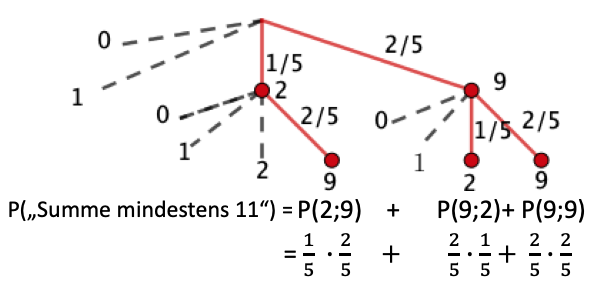
Das Glücksrad wird zweimal gedreht. Bestimmen Sie die Wahrscheinlichkeit dafür, dass die Summe der erzielten Zahlen mindestens $11$ beträgt.

In dieser Aufgabe musst du Wahrscheinlichkeiten von mehrstufigen Zufallsexperimenten am Beispiel eines Glückrades berechnen.
Da die Sektoren gleich groß sind, kannst du davon ausgehen, dass beim einmaligen Drehen jeder Sektor mit der gleichen Wahrscheinlichkeit "gezogen" wird.
Wie die Zahlen den Sektoren zugeordnet sind, ist unerheblich.
Der Ergebnisraum des einmaligen Dreens des Glückrads ist $Ω = {0; 1; 2; 9}$ .
Die obenstehende Graphik ist ein Beispiel, bei dem gerade das Ergebnis $0$ eingetreten ist.
Für die Wahrscheinlichkeiten der Elementarereignisse beim einmaligen Drehen erhältst du dann:
$P (0) = P (1) = P (2) = \frac{1}{5} und P (9) = \frac{2}{5}$ .
Lösung der Teilaufgabe a)
Dass die Reihenfolge der Ergebnisse beim viermaligen Drehen mit $2 \to 0 \to 1 \to 9$ vorgegeben ist, macht die Berechnung der Wahrscheinlichkeit für dieses Ereignis leicht.
Es gilt: $P (2,0,1,9) = \frac{1}{5} \cdot \frac{1}{5} \cdot \frac{1}{5} \cdot \cdot \frac{2}{5}$
$P (2,0,1,9) = \frac{2}{625}$
Begründung:
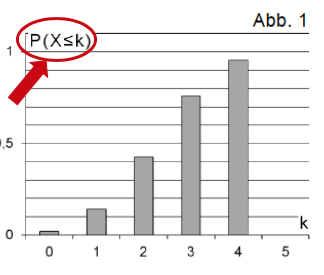
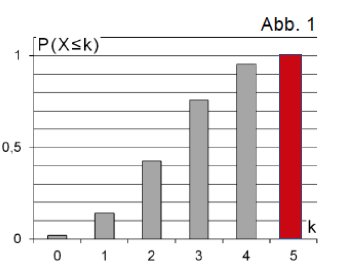
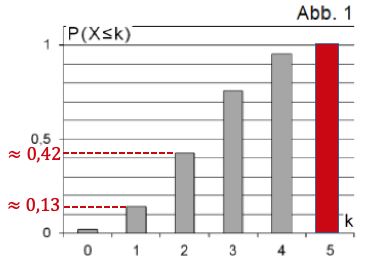
Von einer Drehung zur anschließenden ist das Ergebnis vorgeschrieben und die 1. Pfadregel bei Baumdiagrammen erklärt das Ergebnis.
Du ersparst dir bei dieser Aufgabenstellung allerdings die aufwendige Zeichnung eines vierstufigen Baumdiagramms, da lediglich die Wahrscheinlichkeit eines einzigen (Pfads) zu berechnen ist.
Die Wahrscheinlichkeit, dass beim viermaligen Drehen des Glücksrads die Zahlen in der angegebenen Reihenfolge erscheinen, beträgt 0,32 Prozent.
Lösung der Teilaufgabe b)
Der Ergebnisraum beim zweimaligen Drehen des Glücksrads besteht aus allen geordneten Zahlenpaaren der Zahlen $0,1,2,9$ .
Das Ereignis "Summe mindestens 11"" erfasst die Paare $(2,9), (9,2), (9,9)$ .
Mit der Produktregel und der Summenregel für mehrstufige Experimente erhältst du:
$\begin{array}{rcl} P ("S. mind. 11") & = & P (2,9) + P (9,2) + P (9,9) \\ = & \frac{1}{5} \cdot \frac{2}{5} + \frac{2}{5} \cdot \frac{1}{5} + \frac{2}{5} \cdot \frac{2}{5} \\ = & \frac{8}{25} \end{array}$
Das nachfolgende verkürzt gezeichnete zweistufige Baumdiagramm verdeutlicht die Berechnung.
Ergebnis:
Die Wahrscheinlichkeit, dass die Summe der erzielten Zahlen beim zweimaligen Drehen mindestens $11$ beträgt, ist 32 Prozent.
2
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Gegeben ist eine binomialverteilte Zufallsgröße $X$ mit dem Parameterwert $n = 5$ . Dem Diagramm in Abbildung 1 kann man die Wahrscheinlichkeitswerte $P (X \leq k)$ mit $k \in {0; 1; 2; 3; 4}$ entnehmen.
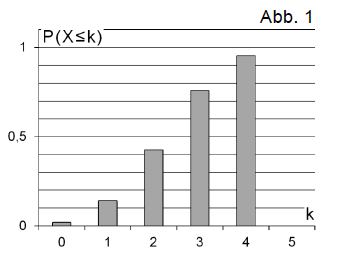
Ergänzen Sie den zu $k = 5$ gehörenden Wahrscheinlichkeitswert $P (X \leq k)$ gehörenden Wahrscheinlichkeitswert im Diagramm. Ermitteln Sie näherungsweise die Wahrscheinlichkeit $P (X = 2)$ .
(2 BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Binomialverteilung
Beachte:
Das gegebene Diagramm zeigt die Summenwahrscheinlichkeiten
$P (X \leq k) = \sum_{i = 0}^{n = k} B (5; p; i)$
an und nicht die lokalen Wahrscheinlichkeiten $P (X = k)$ .
In das gegebene Diagramm ist der Wert für $P (X \leq 5)$ einzuzeichnen.
Es gilt:
$P (X \leq 5) = 1$ .
Die lokale Wahrscheinlichkeit $P (X = 2)$ berechnest du so:
$\begin{array}{l} P (X = 2) = P (X \leq 2) - P (X \leq 1) \end{array}$ $P (X = 2) \approx 0,42 - 0,13$
$P (X = 2) \approx 0,29$
In dieser Aufgabe musst du für eine binomialverteilte Zufallsgröße $X$ Summenwahrscheinlichkeiten von lokalen Wahrscheinlichkeiten unterscheiden.
3
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
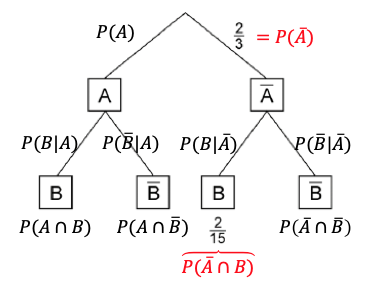
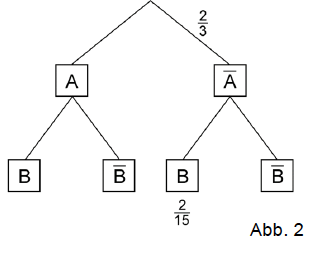
Das Baumdiagramm in Abbildung 2 gehört zu einem Zufallsexperiment mit den stochastisch unabhängigen Ereignissen $A$ und $B$ .
Bestimmen Sie die Wahrscheinlichkeit des Ereignisses $B$ .
(3 BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Stochastische Unabhängigkeit
Gegeben sind die Wahrscheinlichkeiten
$P (A) = \frac{2}{3} und$
$P (A \cap B) = \frac{2}{15}$
Mit diesen Informationen kannst du die Wahrscheinlichkeit von $P (B)$ berechnen. Mit der stochastischen Unabhängigkeit erhälst du
$P (A \cap B) = P (A) \cdot P (B)$
$\frac{2}{15} = \frac{2}{3} \cdot P (B)$
Dividiere nun durch $\frac{2}{3}$ , um $P (B)$ zu erhalten:
$P (B) = \frac{2}{15} : \frac{2}{3} = \frac{1}{5}$
Ergebnis:
Die Wahrscheinlichkeit des Ereignisses $B$ beträgt $\frac{1}{5}$ , also $20$ Prozent.

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

Stochastik, Teil A, Aufgabengruppe 2

Lösung der Teilaufgabe a)

Lösung der Teilaufgabe b)