Geometrie, Teil B, Aufgabengruppe 2

🎓 Prüfungsbereich für Bayern

Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

Die Aufgabenstellung findest du hier zum Ausdrucken als PDF.

1
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
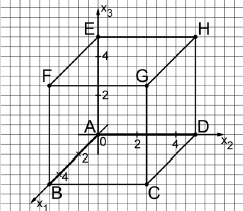
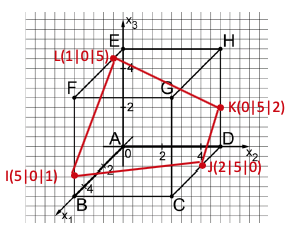
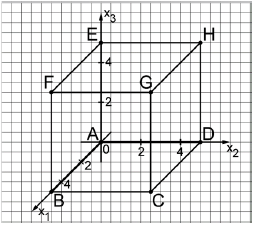
Die Abbildung zeigt den Würfel $A B C D E F G H$ mit $A (0 | 0 | 0)$ und $G (5 | 5 | 5)$ in einem kartesischen Koordinatensystem. Die Ebene $T$ schneidet die Kanten des Würfels unter anderem in den Punkten $I (5 | 0 | 1)$ , $J (2 | 5 | 0)$ , $K (0 | 5 | 2)$ und $L (1 | 0 | 5)$ .
Teilaufgabe a)
(4 BE)
Zeichnen Sie das Viereck $I J K L$ in die Abbildung ein und zeigen Sie, dass es sich um ein Trapez handelt, bei dem zwei gegenüberliegende Seiten gleich lang sind.
Teilaufgabe b)
(3 BE)
Ermitteln Sie eine Gleichung der Ebene $T$ in Normalenform.
(zur Kontrolle: $T : 5 x_{1} + 4 x_{2} + 5 x_{3} - 30 = 0$ )
Für $a \in ℝ^{+}$ ist die Gerade $g_{a}$ : $\vec{x} = (\begin{array}{c} 2,5 \\ 0 \\ 3,5 \end{array}) + λ \cdot (\begin{array}{c} 0 \\ - 10 a \\ \frac{2}{a} \end{array})$ mit $λ \in ℝ$ gegeben.
Teilaufgabe c)
(3 BE)
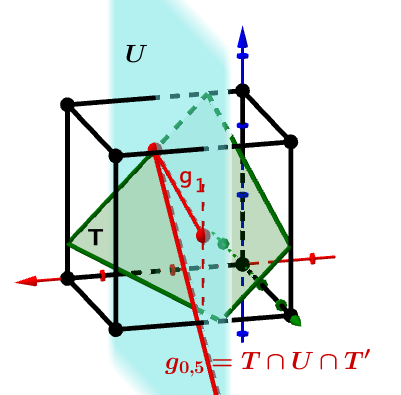
Bestimmen Sie den Wert von $a$ so, dass die Gerade $g_{a}$ die Würfelfläche $C D H G$ in ihrem Mittelpunkt schneidet.
Für jedes $a \in ℝ^{+}$ liegt die Gerade $g_{a}$ in der Ebene $U$ mit der Gleichung $x_{1} = 2,5$ .
Teilaufgabe d)
(2 BE)
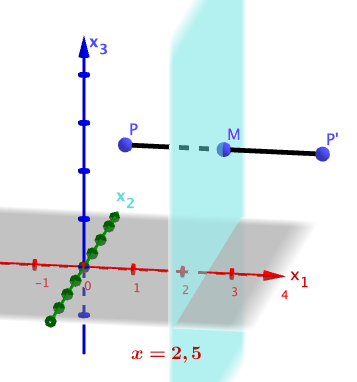
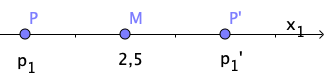
Ein beliebiger Punkt $P (p_{1} | p_{2} | p_{3})$ des Raums wird an der Ebene $U$ gespiegelt. Geben Sie die Koordinaten des Bildpunkts $P^{'}$ in Abhängigkeit von $p_{1}$ , $p_{2}$ und $p_{3}$ an.
Teilaufgabe e)
(4 BE)
Spiegelt man die Ebene $T$ an $U$ , so erhält man die von $T$ verschiedene Ebene $T^{'}$ . Zeigen Sie, dass für einen bestimmten Wert von $a$ die Gerade $g_{a}$ in der Ebene $T$ liegt, und begründen Sie, dass diese Gerade $g_{a}$ die Schnittgerade von $T$ und $T^{'}$ ist.
Teilaufgabe f)
(4 BE)
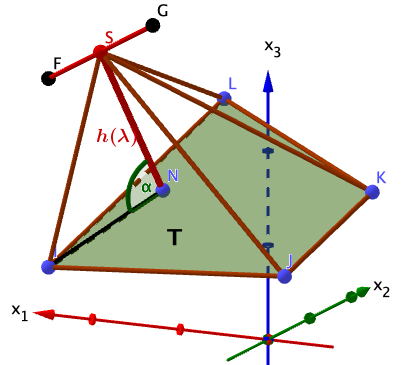
Die Spitze einer Pyramide mit der Grundfläche $I J K L$ liegt auf der Kante $[F G]$ . Untersuchen Sie, ob die Höhe dieser Pyramide $2$ betragen kann.

Im Zusammenhang mit einem gegebenen Würfel sind im Raum Lagebeziehungen von Punkten, Geraden und Ebenen zu untersuchen. Eine Ebene ist zu spiegeln. Eine Eigenschaft einer Pyramide ist zu untersuchen.
$ABCDEFGH$ ist ein Würfel.
Gegeben sind die Eckpunkte
$A (0 | 0 | 0)$ und $G (5 | 5 | 5)$ .
Lösung Teilaufgabe a)
(4 BE)
Es ist zu zeigen, dass das Viereck
$I (5 | 0 | 1)$ , $J (2 | 5 | 0)$ , $K (0 | 5 | 2)$ und $L (1 / 0 / 5)$ ein Trapez mit gleich langen Gegenseiten ist.
Beachte, dass die Eckpunkte "gittergenau" eingezeichnet werden!
So argumentierst du am zeitsparendsten:
Die Seiten $[I L]$ und $[J K]$ sind die parallelen Grundseiten des Vierecks $I J K L$ da sie in parallelen Gegenflächen des Würfels liegen und die längere doppelt so lang ist wie die kürzere:
Da gilt $\vec{I L} = (\begin{array}{c} 1 \\ 0 \\ 5 \end{array}) - (\begin{array}{c} 5 \\ 0 \\ 1 \end{array}) = (\begin{array}{c} - 4 \\ 0 \\ 4 \end{array})$
und
$\vec{J K} = (\begin{array}{c} 0 \\ 5 \\ 2 \end{array}) - (\begin{array}{c} 2 \\ 5 \\ 0 \end{array}) = (\begin{array}{c} - 2 \\ 0 \\ 2 \end{array})$ .
Damit ist gezeigt, dass das Viereck ein Trapez ist.
Für seine Schenkel $[I J]$ und $[L K]$ gilt:
$I J = | \vec{I J} | = | (\begin{array}{c} 2 \\ 5 \\ 0 \end{array}) - (\begin{array}{c} 5 \\ 0 \\ 1 \end{array}) | = | (\begin{array}{c} - 3 \\ 5 \\ - 1 \end{array}) |$
$L K = | \vec{L K} | = | (\begin{array}{c} 0 \\ 5 \\ 2 \end{array}) - (\begin{array}{c} 1 \\ 0 \\ 5 \end{array}) | = | (\begin{array}{c} - 1 \\ 5 \\ - 3 \end{array}) |$
Da beide Schenkel die gleichen Vektorkomponenten (nur in verschiedener Reihenfolge) haben, erkennst und begründest du ohne weitere Rechnung, dass beide Schenkel gleich lang sind und das Trapez somit gleichschenklig ist.
Lösung Teilaufgabe b)
(3 BE)
Nachdem in Teilaufgabe a) festgestellt wurde, dass die vier Punkte $I, J, K, L$ tatsächlich in einer Ebene $T$ liegen, kann deren Normalengleichung aufgestellt werden.
Zum Beispiel über das Kreuzprodukt der Vektoren $\vec{I J}$ und $\vec{I L}$ .
$\vec{I J} \times \vec{I L} = (\begin{array}{c} - 3 \\ 5 \\ - 1 \end{array}) \times (\begin{array}{c} - 4 \\ 0 \\ 4 \end{array}) = (\begin{array}{c} 5 \cdot 4 - (- 1) \cdot 0 \\ (- 1) \cdot (- 4) - (- 3) \cdot 4 \\ (- 3) \cdot 0 - 5 \cdot (- 4) \end{array}) = (\begin{array}{c} 20 \\ 16 \\ 20 \end{array})$
$(\begin{array}{c} 20 \\ 16 \\ 20 \end{array}) = 4 \cdot (\begin{array}{c} 5 \\ 4 \\ 5 \end{array})$
$\vec{n} = (\begin{array}{c} 5 \\ 4 \\ 5 \end{array})$ verwendest du als Normalenvektor zum Aufstellen der Normalengleichung.
Es gilt:
$T : \vec{n} \circ [\vec{x} - \vec{O I}] = 0$
$T : (\begin{array}{c} 5 \\ 4 \\ 5 \end{array}) \circ [\vec{x} - (\begin{array}{c} 5 \\ 0 \\ 1 \end{array})] = 0$
Ausmultipliziert ergibt dies:
$T : 5 \cdot (x_{1} - 5) + 4 \cdot (x_{2} - 0) + 5 \cdot (x_{3} - 1) = 0$
$T : 5 x_{1} + 4 x_{2} + 5 x_{3} - 30 = 0$
Lösung Teilaufgabe c)
(3 BE)
Für einen bestimmten positiven Wert von $a$ ist die Gerade $g_{a} : \vec{x} = (\begin{array}{c} 2,5 \\ 0 \\ 3,5 \end{array}) + λ \cdot (\begin{array}{c} 0 \\ - 10 a \\ \frac{2}{a} \end{array})$ mit $λ \in ℝ$ gegeben, die mit dem Mittelpunkt der rechten Würfelfläche zu schneiden ist.
Für welchen Wert von $a$ trifft dies zu?
Mittelpunkt $M$ der quadratischen Würfelfläche $C D H G$ ist der Schnittpunkt der Diagonalen. Und da sich diese gegenseitig halbieren, genügt es, den Mittelpunkt einer Diagonalen, z.B. von $[G D]$ , zu ermitteln.
Der Mittelpunkt einer Strecke errechnet sich als arithmetisches Mittel der Koordinaten der Endpunkte.
Somit erhältst du:
$\vec{O M} = \frac{1}{2} [(\begin{array}{c} 5 \\ 5 \\ 5 \end{array}) + (\begin{array}{c} 0 \\ 5 \\ 0 \end{array})] = (\begin{array}{c} 2,5 \\ 5 \\ 2,5 \end{array})$
Also ist $M (2,5 | 5 | 2,5)$ .
Jetzt setzt du $M (2,5 | 5 | 2,5)$ als Punkt in die Geradengleichung für $g_{a}$ ein und löst die Gleichung nach $a$ auf.
$M \in g_{a}$ :
$(\begin{array}{c} 2,5 \\ 5 \\ 2,5 \end{array}) = (\begin{array}{c} 2,5 \\ 0 \\ 3,5 \end{array}) + λ \cdot (\begin{array}{c} 0 \\ - 10 a \\ \frac{2}{a} \end{array})$
$\begin{array}{rrcll} I & 2,5 & = & 2,5 \\ II & 5 & = & 0 + λ \cdot (- 10 a) \\ III & 2,5 & = & 3,5 + λ \cdot \frac{2}{a} \\ I I^{'} & λ & = & - \frac{1}{2 a} \\ I I I^{'} & λ & = & - \frac{a}{2} \\ I I^{'} = I I I^{'} : & - \frac{1}{2 a} & = & - \frac{a}{2} & | \cdot 2 a \\ a^{2} & = & 1 \Rightarrow \\ a & = & + 1 da a \in ℝ^{+} \end{array}$
Ergebnis:
Für $a = + 1$ schneidet die Gerade $g_{a}$ die Würfelfläche $C D H G$ in ihrem Mittelpunkt.
Lösung Teilaufgabe d)
(2 BE)
Spiegelst du einen Punkt $P (p_{1} | p_{2} | p_{3})$ an der Ebene $U : x_{1} = 2,5$ , dann ist der Schnittpunkt $M$ der Strecke $[P P^{'}]$ mit $U$ der Mittelpunkt von $[P P^{'}]$ .
Dabei gilt:
$p_{2}^{'} = p_{2}$ und
$p_{3}^{'} = p_{3}$ .
$p_{1}^{'}$ berechnest du aus dem Ansatz für das arithmetische Mittel aus folgender Skizze:
Es gilt:
$p_{1}^{'} = 5 - p_{1}$
Ergebnis:
Die Koordinaten eines Bildpunktes $P^{'} (p_{1}^{'} | p_{2}^{'} | p_{3}^{'})$ in Abhängigkeit des Punktes $P (p_{1} | p_{2} | p_{3})$ sind:
$p_{1}^{'} = 5 - p_{1}$
$p_{2}^{'} = p_{2}$
$p_{3}^{'} = p_{3}$ .
Lösung Teilaufgabe e)
(4 BE)
Es ist
$g_{a} : \vec{x} = (\begin{array}{c} 2,5 \\ 0 \\ 3,5 \end{array}) + λ \cdot (\begin{array}{c} 0 \\ - 10 a \\ \frac{2}{a} \end{array}); λ \in ℝ; a \in ℝ^{+}$ .
$T : 5 x_{1} + 4 x_{2} + 5 x_{3} - 30 = 0$
Bedingungen dafür, dass eine Gerade $g_{a}$ in der Ebene $T$ liegt sind:
Der Aufpunkt $(2,5 | 0 | 3,5)$ liegt in $T$ und der Richtungsvektor von $g_{a}$ ist senkrecht zum Normalenvektor von $T$ .
Setze $(2,5 | 0 | 3,5)$ in die Gleichung von $T$ ein:
$\begin{aligned} 5 \cdot 2,5 + 4 \cdot 0 + 5 \cdot 3,5 - 30 & \overset{?}{=} 0 \\ 0 & \overset{!}{=} 0 \Rightarrow \\ (2,5 | 0 | 3,5) \in T . \end{aligned}$
Setze nun das Skalarprodukt des Richtungsvektors von $g_{a}$ und dem Normalenvektor von $T$ gleich null:
$\begin{array}{rcll} (\begin{array}{c} 0 \\ - 10 a \\ \frac{2}{a} \end{array}) \circ (\begin{array}{c} 5 \\ 4 \\ 5 \end{array}) & = & 0 \\ - 40 a + \frac{10}{a} & = & 0 & | \cdot a \\ - 40 a^{2} + 10 & = & 0 & | - 10 | : (- 40) \\ a^{2} & = & \frac{1}{4} & | \sqrt{(}) \\ a & = & + \frac{1}{2} \\ (a & = & - \frac{1}{2}) \end{array}$
Ergebnis:
Für $a = + \frac{1}{2}$ liegt die Gerade $g_{a}$ in der Ebene $T$ .
Wie bereits in Teilaufgabe c) gezeigt, ist $g_{0,5}$ eine Gerade aus der Ebene $U$ .
Und da $T$ an $U$ gespiegelt wird, ist $g_{0,5}$ Fixgerade der Spiegelung und damit auch Gerade von $T^{'}$ , also Schnittgerade von $T$ und $T^{'}$ .
Die folgende Zeichnung veranschaulicht die Zusammenhänge.
Alternative Begründung der Schnitteigenschaft von $g_{0,5}$
Mit dem Ergebnis der Teilaufgabe d) erhältst du leicht die Normalengleichung von $T^{'}$ .
Aus
$T : 5 x_{1} + 4 x_{2} + 5 x_{3} - 30 = 0$
wird durch die Spiegelung
$x_{1} = 5 - x_{1}^{'} x_{2} = x_{2}^{'} x_{3} = x_{3}^{'}$
$T^{'} : 5 \cdot (5 - x_{1}^{'}) + 4 x_{2}^{'} + 5 x_{3}^{'} - 30 = 0$
und somit
$T^{'} : - 5 x_{1} + 4 x_{2} + 5 x_{3} - 5 = 0$ .
Da zum Beispiel die beiden Punkte aus $g_{0,5}$ für $λ = 0$ und $λ = 1$ , $(2,5 | 0 | 3,5)$ und $(2,5 | - 5 | 7,5)$ , die Gleichung von $T^{'}$ erfüllen, gilt $g_{0,5} \subset T^{'}$ .
Alternative Bestimmung der Geraden $g_{0,5}$
Du kannst die Vektorkomponenten der Vektorgleichung von $g_{a}$ direkt in die Normalengleichung von $T$ einsetzen und zeigen, dass die entstehende Gleichung nur für $a = 0,5$ erfüllt wird.
Du erhältst die Gleichung
$5 \cdot 2,5 + 4 \cdot (0 - 10 a λ) + 5 \cdot (3,5 + \frac{2}{a} \cdot λ) - 30 = 0.$
Somit:
$\begin{array}{rcll} - 40 a λ + \frac{10}{a} \cdot λ & = & 0 & | \cdot a \\ - 40 a^{2} \cdot λ + 10 λ & = & 0 & | : (- 10) \\ λ \cdot (4 a^{2} - 1) & = & 0 & | : λ \neq 0 \\ 4 a^{2} - 1 & = & 0 & | + 1 | : 4 \\ a^{2} & = & \frac{1}{4} & | \sqrt{(}) \\ a & = & + \frac{1}{2} \end{array}$
Lösung Teilaufgabe f)
(4 BE)
Die Grundfläche der Pyramide liegt in der Ebene Die Spitze $S$ liegt auf der Strecke $[F G]$ .
Die Höhe $h$ einer Pyramide ist der Abstand der Spitze von der Grundfläche.
Dieser Abstand kann mit der Hesse Normalenform der Ebenengleichung der Grundfläche berechnet werden.
Es ist:
$H N F (T) : \frac{5 x_{1} + 4 x_{2} + 5 x_{3} - 30}{\sqrt{66}} = 0$
Mit $F (5 | 0 | 5)$ und $G (5 | 5 | 5)$ stellst du die Vektorgleichung der Strecke $[F G]$ auf.
$[F G] : \vec{x} = (\begin{array}{c} 5 \\ 0 \\ 5 \end{array}) + λ \cdot (\begin{array}{c} 0 \\ 5 \\ 0 \end{array}); 0 \leq λ \leq 1$
Eine mögliche Spitze $S$ der Pyramide hat dann die Koordinaten $(5 | 5 λ | 5)$ .
Für deren Abstand von der Ebene $T$ - und damit für die Höhe $h (λ)$ der Pyramide gilt:
$h (λ) = \frac{5 \cdot 5 + 4 \cdot 5 λ + 5 \cdot 5 - 30}{\sqrt{66}}$
$h (λ) = \frac{20 + 20 λ}{\sqrt{66}}$
Die kleinste Pyramidenhöhe für einen Punkt $S$ auf der Strecke $[F G]$ ergibt sich für $F = S$ mit
$h (0) = \frac{20}{\sqrt{66}} \approx 2,46.$
Für jeden anderen Punkt auf $[F G]$ ist die Pyramidenhöhe noch größer.
Ergebnis:
Für keinen Punkt auf der Kante $[F G]$ kann die Höhe der Pyramide $2$ betragen.