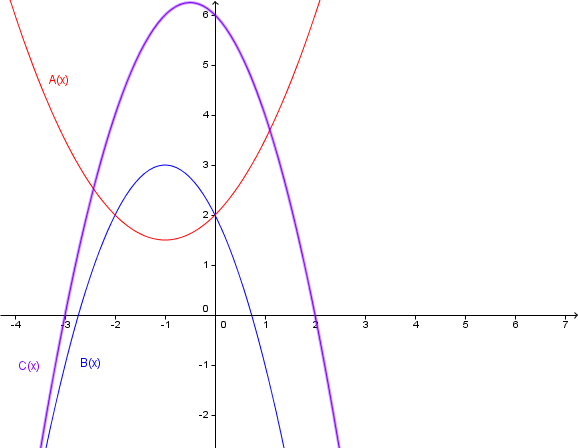
Welcher Graph gehört zu welcher Funktion? Begründe deine Entscheidung!
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 mit Namensnennung von Herrn Rudolf Brinkmann → Was bedeutet das?
Welcher Graph gehört zu welcher Funktion? Begründe deine Entscheidung!
