Gemischte Aufgaben zu Funktionen
Hier findest du gemischte Aufgaben zu Funktionen. Lerne, Graphen zu skizzieren, Funktionsterme zu bestimmen und weitere Größen von Funktionen zu berechnen!
- 1
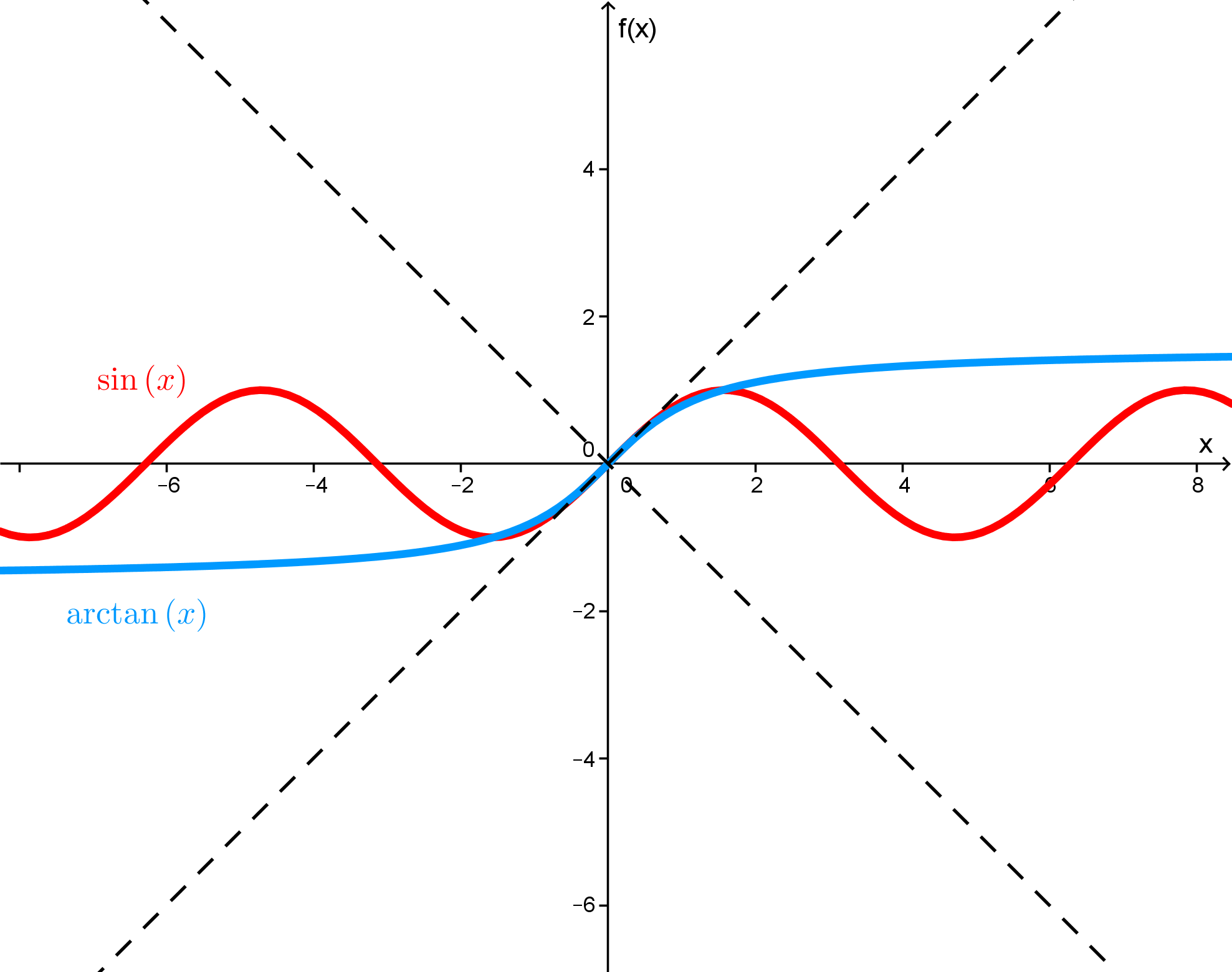
Gib den Term einer Funktion an, die folgende Bedingungen erfüllt.
Die Funktion geht für gegen ;
der Graph der Funktion ist streng monoton steigend;
die Funktion ist stetig.
- 2
Gegeben ist der Graph der Funktion . Skizziere den Graphen der Funktion .
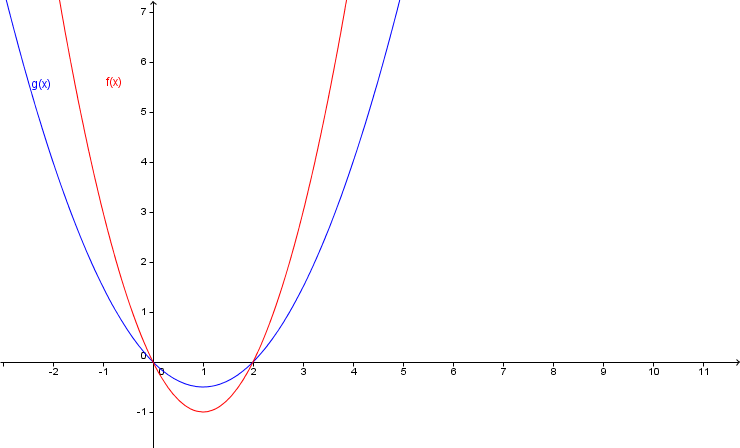
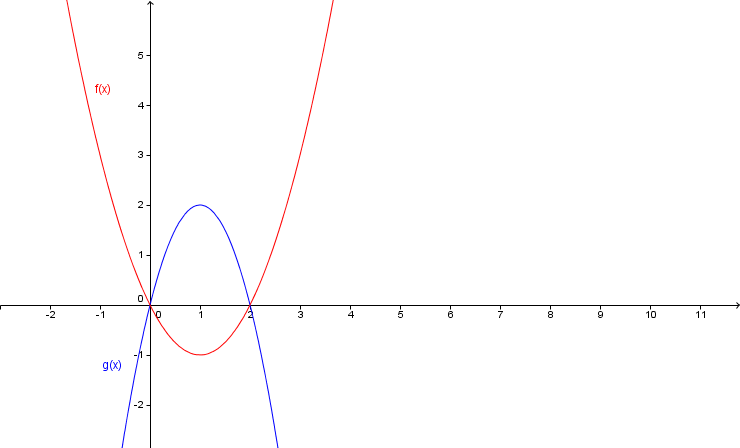
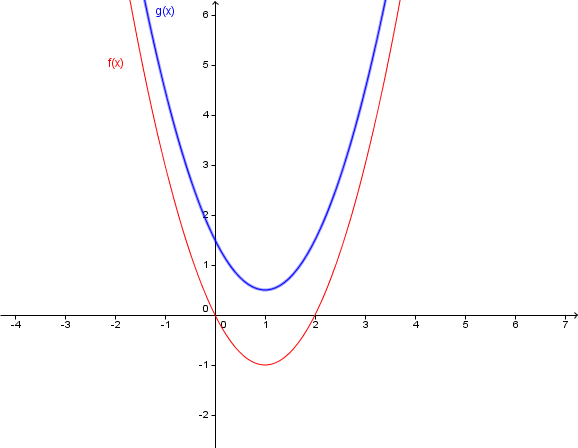
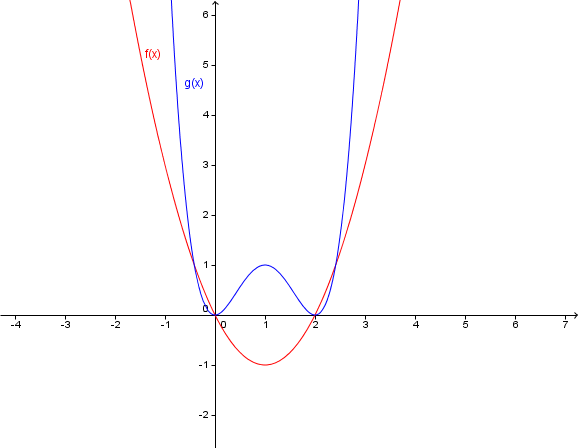
- 3
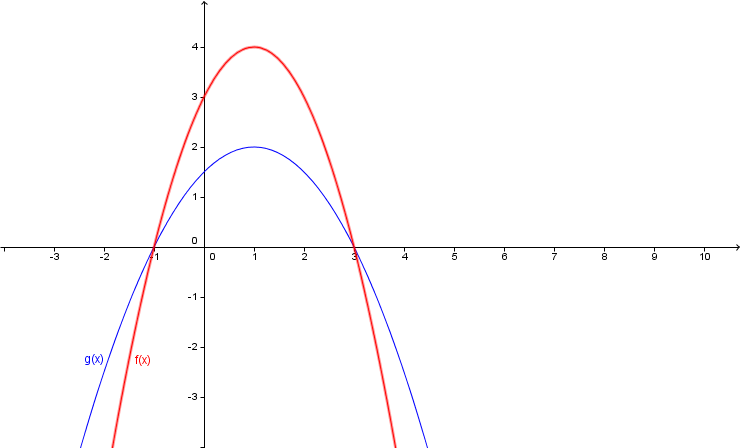
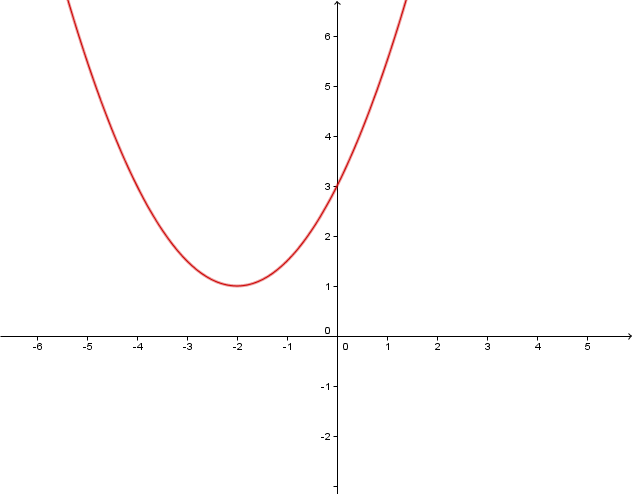
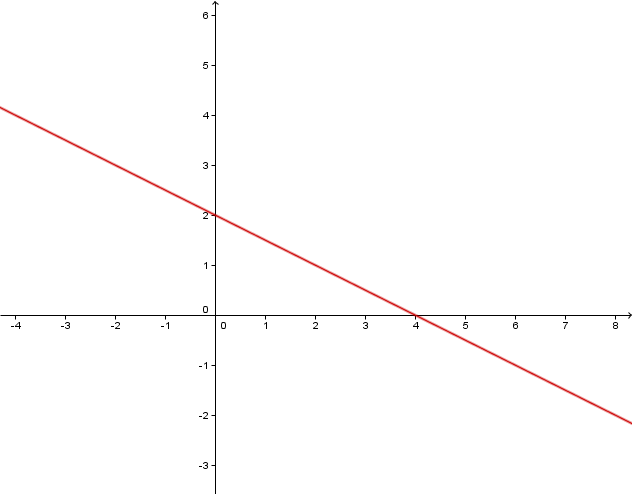
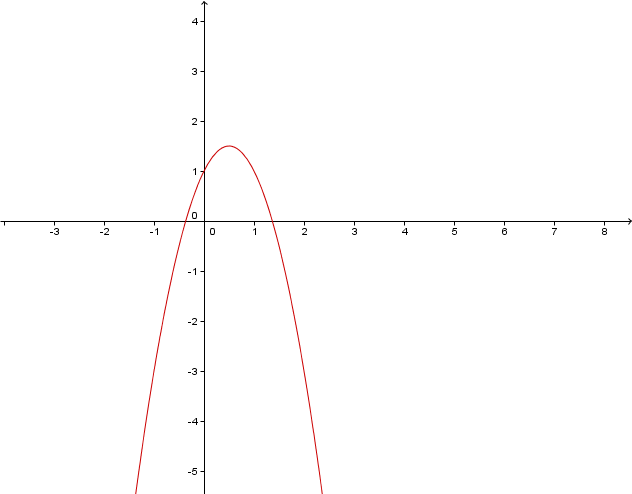
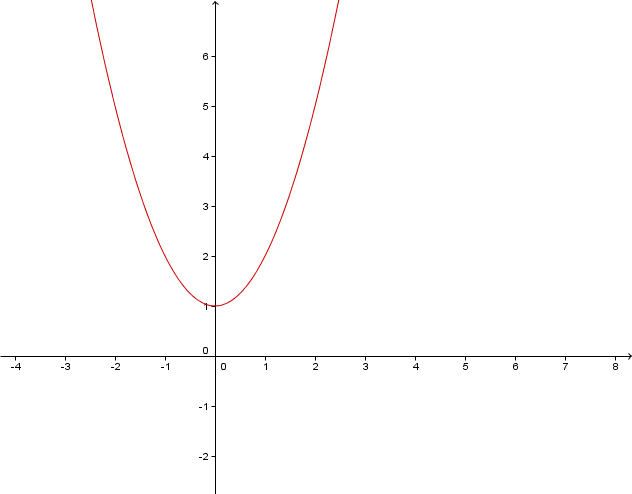
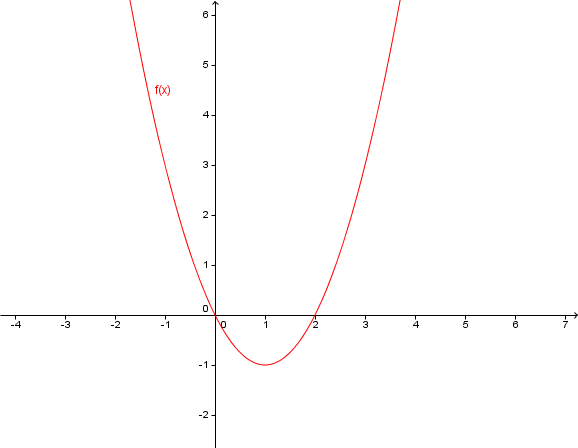
Welcher Graph gehört zu welcher Funktion? Begründe deine Entscheidung!
- 4
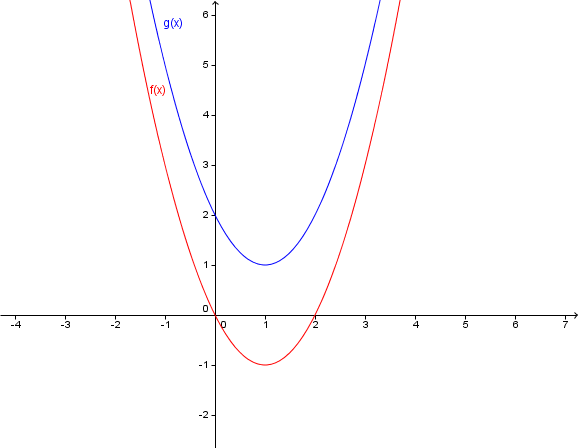
Welcher Zusammenhang besteht zwischen den Graphen von und ?
Stelle die Scheitelpunktgleichungen auf und vergleiche diese.
- 5
Ordne jedem Funktionsgraphen einen der folgenden Funktionsterme zu.
- 6
Gibt es stetige Funktionen mit den folgenden Eigenschaften? Falls ja, gib ein Beispiel an; falls nein, begründe deine Entscheidung.
- 7
Berechne die Tangente an den Graphen der gegebenen Funktion zum gegebenen Punkt .
- 8
Gegeben ist die Funktion .
Erkläre, wie der Funktionsterm aus entstanden ist.
- 9
Gib den Term einer nicht-linearen Funktion an, für die gilt: . Mache deine Wahl plausibel.
- 10
Begründe kurz, warum folgende Aussagen gelten.
Ist der Graph einer in definierten, integrierbaren Funktion punktsymmetrisch zum Ursprung, dann gilt für alle :
- 11
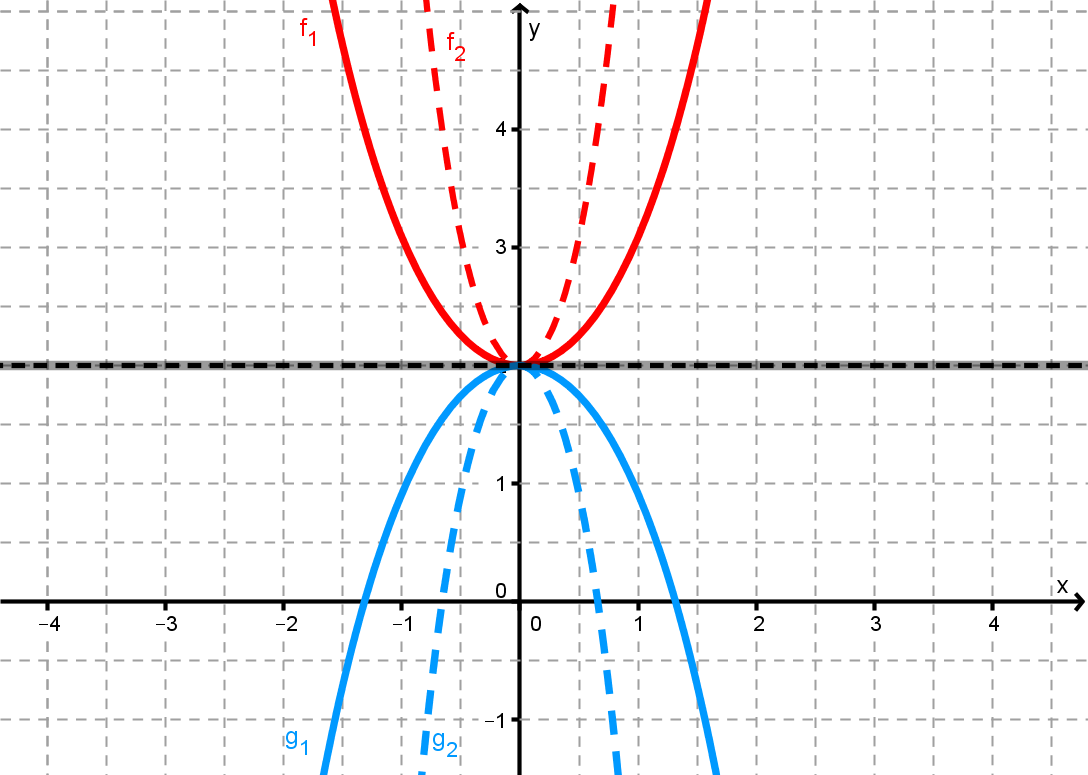
Ordne die auf definierten Funktionen mit einer kurzen Begründung den Graphen zu.
a)
b)
c)

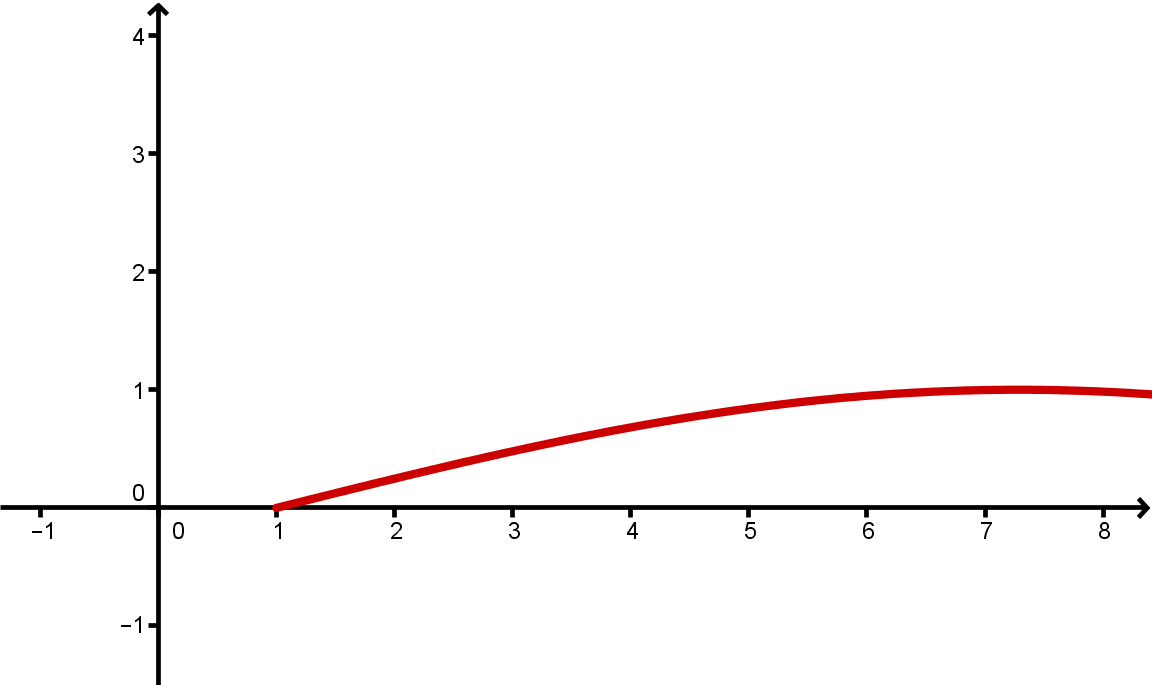

- 12
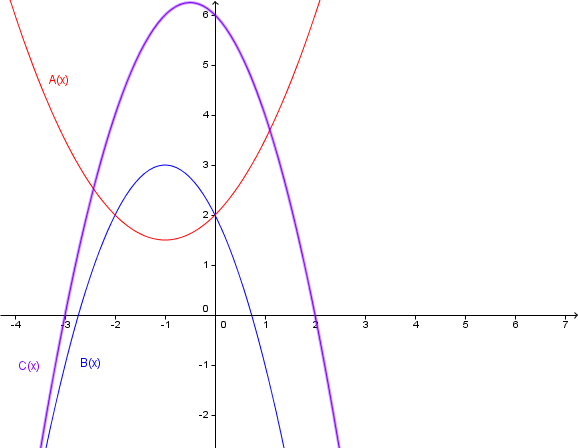
Ordne die Funktionen und den Graphen zu und begründe deine Wahl kurz.
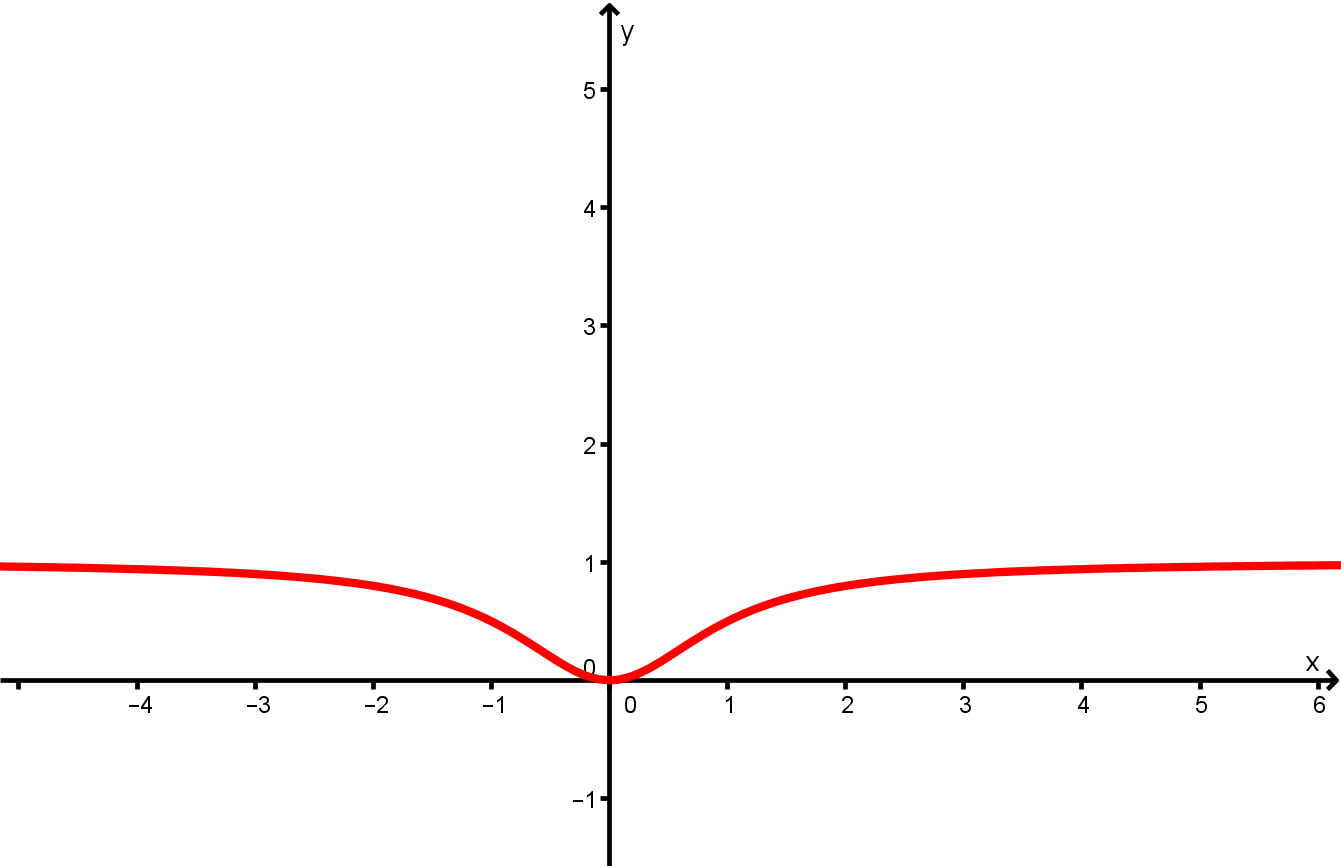
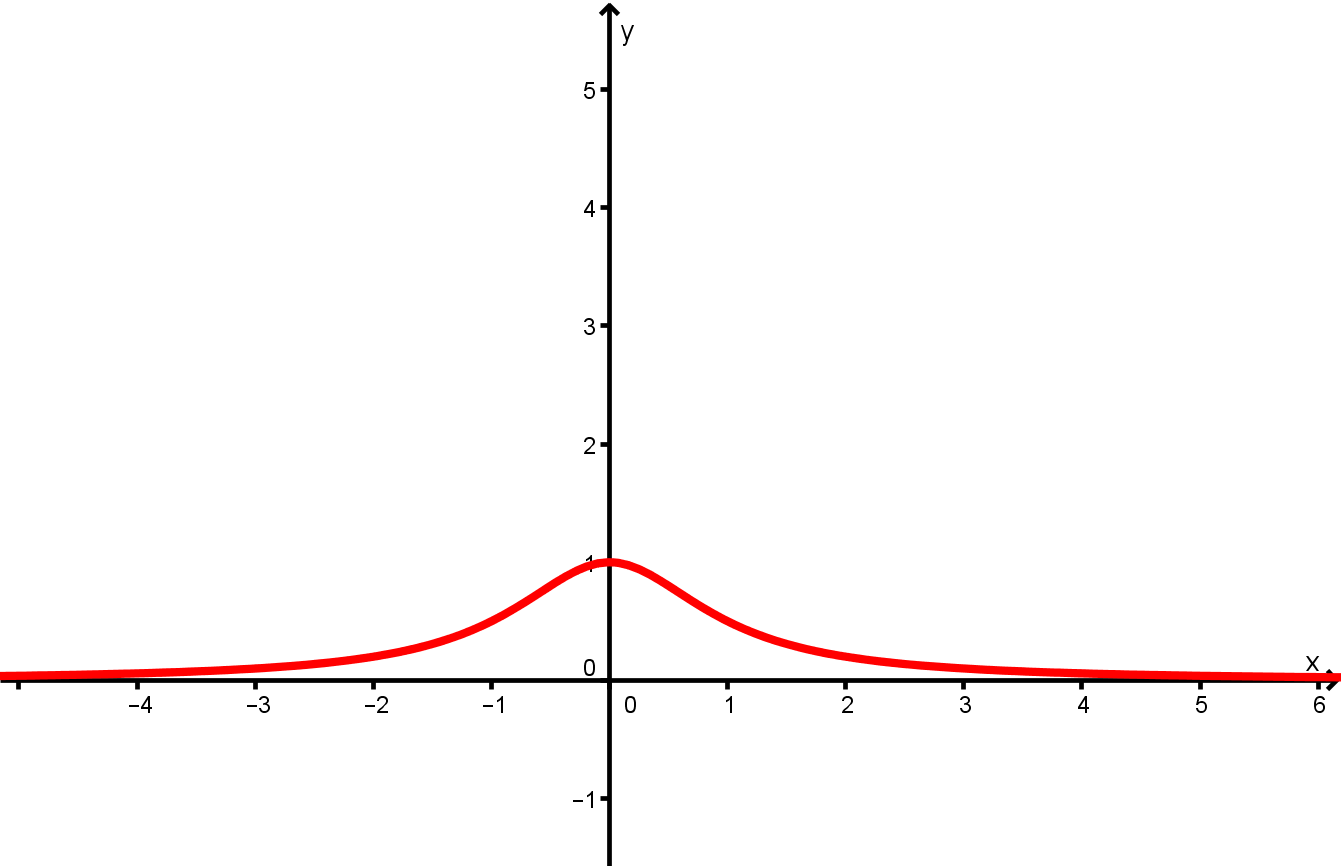
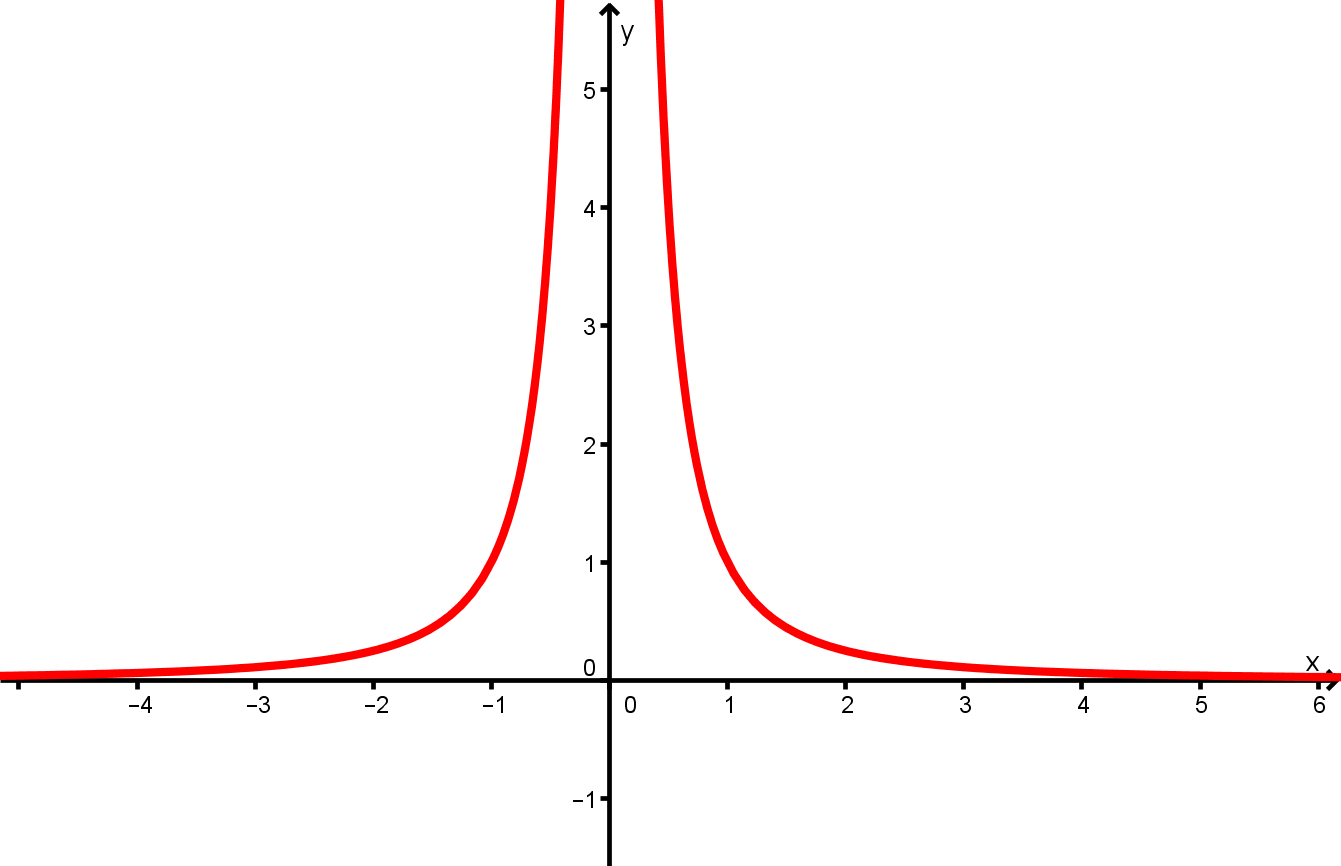
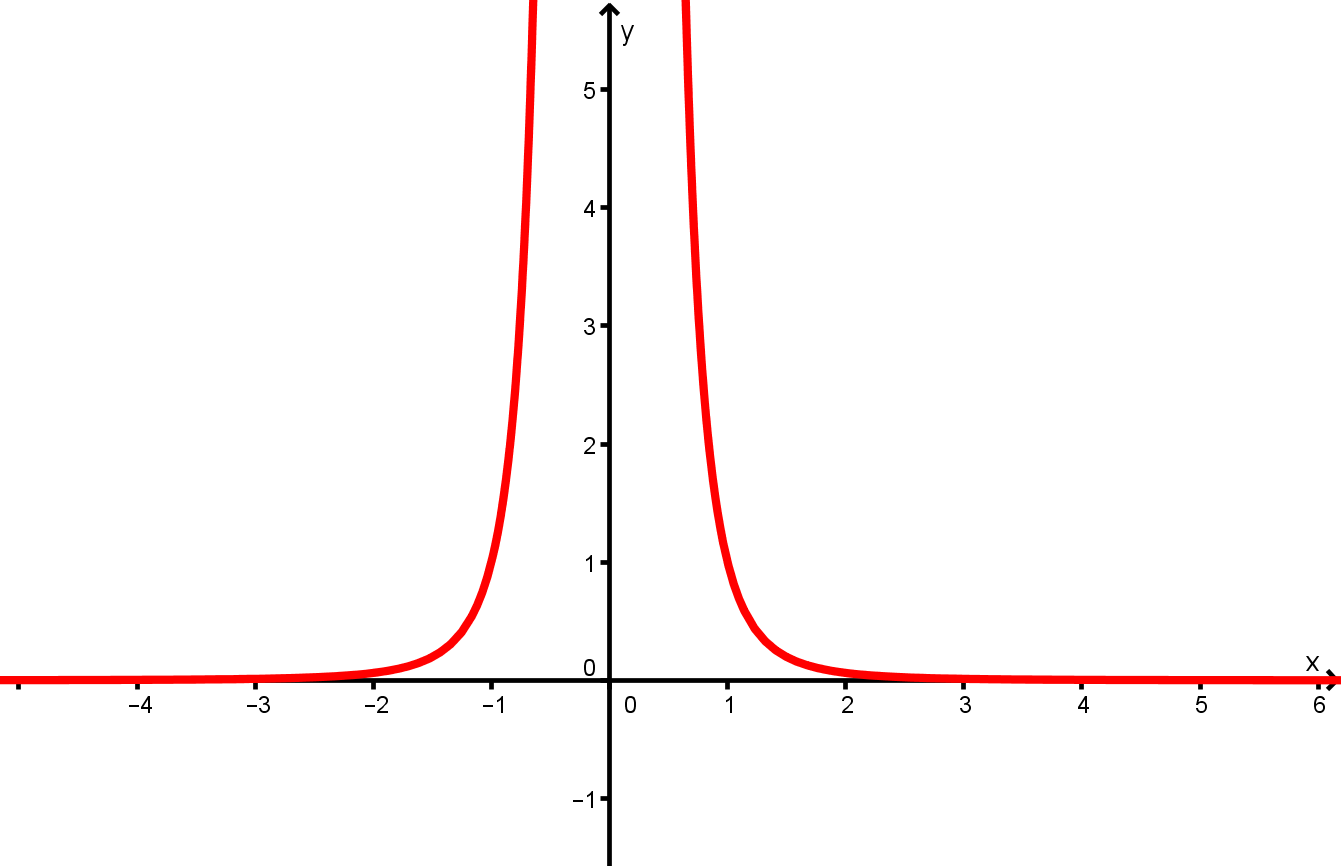
- 13
Betrachte die Funktion . Der Graph der Funktion ist und ihr Definitionsbereich .
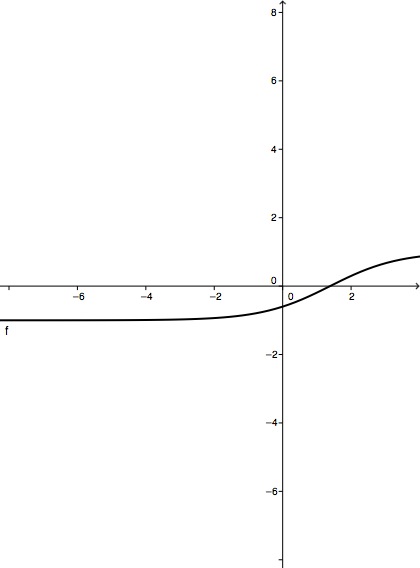
Berechne die Koordinaten des Schnittpunkts von mit der y-Achse.
Berechne anschließend die Koordinaten des Schnittpunkts von mit der x-Achse.
Bestimme das Verhalten von für und .
Untersuche das Monotonieverhalten von mit Hilfe der ersten Ableitung von .
ist der einzige Wendepunkt von . Zeige, dass die Gerade mit der Gleichung durch verläuft und auf der Wendetangente senkrecht steht.
Verschiebe um nach links, um den Graphen zu erhalten und gib an. Zeige, dass punktsymmetrisch zum Ursprung ist. Welche Bedeutung hat in diesem Fall der Punkt für ?
- 14
Gegeben ist die Funktion mit .
Gib die Definitionsmenge , die Gleichung aller Asymptoten und das Verhalten an den Rändern des Definitionsbereichs an.
Untersuche die angegebene Funktion auf Symmetrie.
Untersuche die Funktion auf gemeinsame Punkte mit den Koordinatenachsen.
Untersuche das Monotonieverhalten der Funktion und gib Lage und Art aller Extremstellen an.
Zeige, dass eine Stammfunktion von ist und bestimme den Funktionsterm derjenigen Stammfunktion, die durch den Punkt verläuft.
- 15
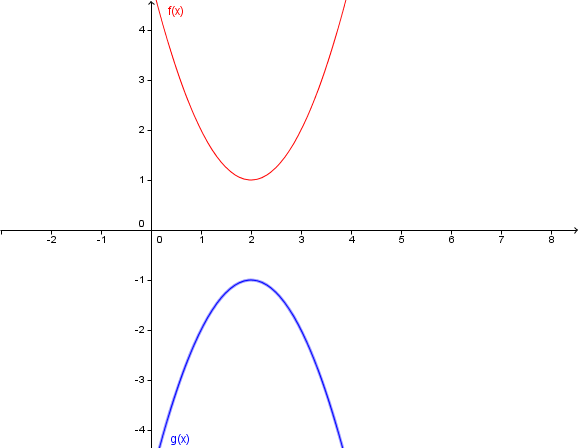
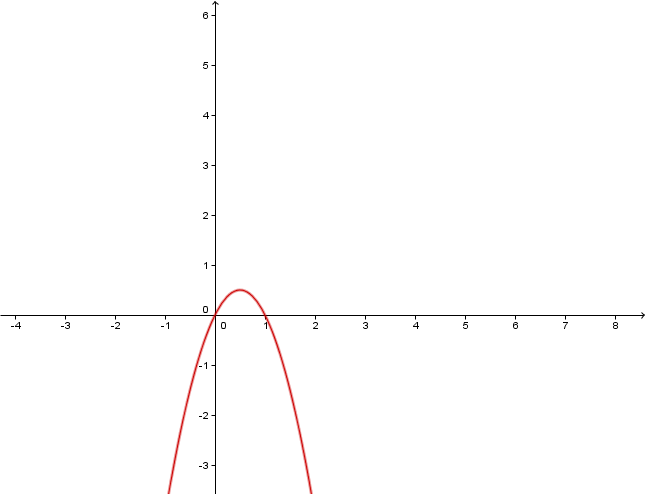
Für jedes ist die Funktion definiert durch .
Begründe, dass die Funktionenschar den gemeinsamen Punkt besitzt.
Begründe außerdem ohne abzuleiten, dass ein globales Minimum ist. Als mögliche Hilfestellung erhältst du die Graphen der Funktionen und .
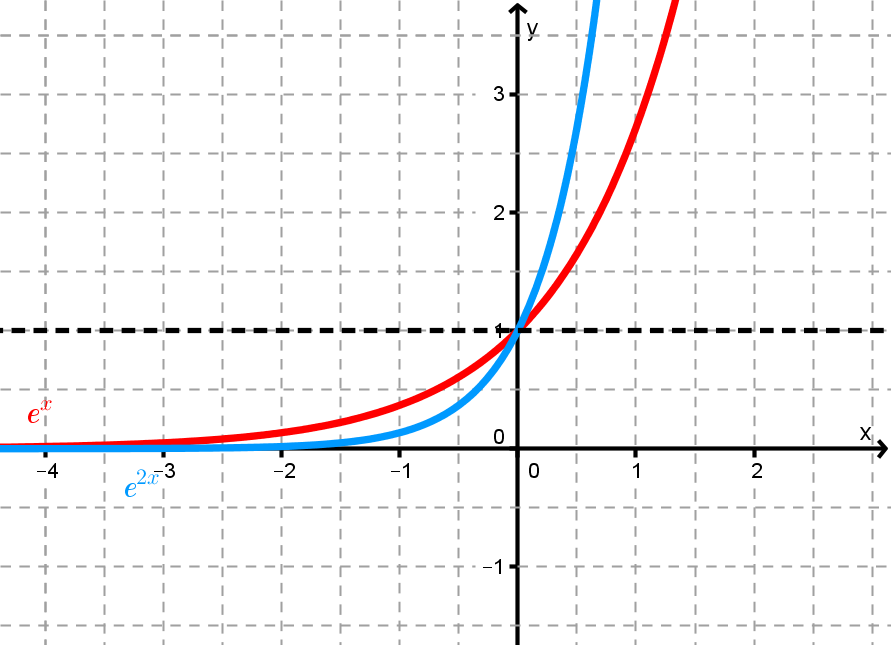
werde an der Gerade gespiegelt. Gib den Funktionsterm der neuen Funktionenschar an.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?