Teil A

🎓 Prüfungsbereich für Bayern

Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

Die Aufgabenstellung findest du hier zum Ausdrucken als PDF.

1
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Es werden zwei Versuche zur Abkühlung von heißem Wasser durchgeführt. Der Temperaturverlauf während dieser Versuche lässt jeweils näherungsweise durch eine Exponentialfunktion der Form
$\displaystyle y=(y_A-y_U)\cdot0{,}9^x+y_U \\ \left(\mathbb{G}=\mathbb{R}^+ \times \mathbb{R}^+,~ y_A \in \mathbb{R}^+,~ y_U \in \mathbb{R}^+\right)$
beschreiben. Dabei ist nach $x$ Minuten die Temperatur des Wassers auf $y\mathrm{°C}$ gesunken. Die Anfangstemperatur des Wassers beträgt $y_A\mathrm{°C}$ und die Umgebungstemperatur $y_U\mathrm{°C}$ . Runden Sie im Folgenden auf eine Stelle nach dem Komma.
1. Im ersten Versuch kühlt $95\mathrm{°C}$ heißes Wasser in einem Raum mit einer Umgebungstemperatur von $20\mathrm{°C}$ ab. Berechnen Sie, nach welcher Zeit die Wassertemperatur auf $60\mathrm{°C}$ gesunken ist.
  Minuten
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Wachstumsaufgaben
  Die Temperatur soll nach $x$ Minuten $60\mathrm{°C}$ erreichen.
  Daraus ergibt sich folgende Gleichung:
  $\displaystyle \def\arraystretch{1.25} \begin{array}{rcl} 60&=&(95-20)\cdot 0{,}9^x +20\\ 40&=&75\cdot 0{,}9^x\\ \frac{40}{75}&=&0{,}9^x\\ \log_{0{,}9}\frac{40}{75}&=&x\\ x&\approx&5{,}97 \end{array}$
  Bei Rundung auf eine Nachkommastelle ergibt sich, dass die Wassertemperatur nach $6,0$ Minuten auf $60\mathrm{°C}$ gefallen ist.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Im zweiten Versuch kühlt $72\mathrm{°C}$ heißes Wasser in einem ersten Raum mit einer Umgebungstemperatur von $18\mathrm{°C}$ für $3$ Minuten ab. Anschließend wird der Abkühlvorgang in einem zweiten Raum für weitere $8$ Minuten fortgesetzt, bis das Wasser eine Temperatur von $39\mathrm{°C}$ besitzt. Berechnen Sie die Umgebungstemperatur im zweiten Raum.
  °C
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Wachstumsaufgaben
  Zunächst musst du die Temperatur nach 3 Minuten berechnen; setze dazu in die Gleichung ein:
  $\displaystyle \def\arraystretch{1.25} \begin{array}{rcl} y&=&(72-18)\cdot 0{,}9^3 +18\\ y&\approx&57{,}4\text{°C} \end{array}$
  Daraufhin setzt du den veränderten Startwert in die Gleichung ein und löst nach der Umgebungstemperatur auf:
  $\displaystyle \def\arraystretch{1.25} \begin{array}{rcl} 39&=&(57{,}4-y_U)\cdot 0{,}9^8 +y_U\\ 39-y_U&=&(57{,}4-y_U)\cdot 0{,}9^8\\ 39-y_U&\approx&(57{,}4-y_U)\cdot 0{,}430\\ 39-y_U&=&24{,}71-0{,}430y_U\\ 14{,}29&=&0{,}57y_U\\ y_U&=&25{,}07 \end{array}$
  Die Umgebungstemperatur $y_{U}$ beträgt also $25{,}1\mathrm{°C}$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉

Das gleichschenklige Dreieck $A B C$ mit der Basis $[B C]$ und der Höhe $[A M]$ ist die Grundfläche der Pyramide $A B C S$ mit der Spitze $S$ . Der Punkt $D \in [AM]$ ist der Fußpunkt der Pyramidenhöhe $[D S]$ , die senkrecht auf der Grundfläche steht.

Es gilt: $\overline{AM}=8 \ \text{cm};\overline{BC}=10\ \text{cm};\;\overline{AD}=4{,}5\ \text{cm};\overline{DS}=8{,}5\ \text{cm}.$

Die untenstehende Zeichnung zeigt ein Schrägbild der Pyramide $A B C S$ .

In der Zeichnung gilt: $q=\frac12;\;\;\omega=45^\circ$ . $[A M]$ liegt auf der Schrägbildachse.

Runden Sie im Folgenden auf zwei Stellen nach dem Komma.

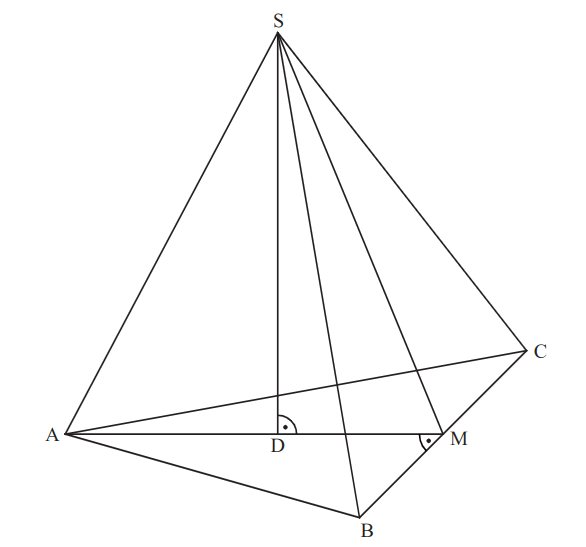
Berechnen Sie das Maß des Winkels $\angle MAC$ .
[Ergebnis: $\angle MAC=32{,}01^\circ$ ]

Maß des Winkels $\measuredangle MAC$ im rechtwinkligen Dreiecks AMC (grün) mithilfe der Trigonometrie:
$\tan\left(\measuredangle MAC\right)=\frac{Gegenkathete}{Ankathete}=\frac{\overline{MC}}{\overline{AM}}$
$\tan\left(\measuredangle MAC\right)=\dfrac{5\;\text{cm}}{8\;\text{cm}}$
$\tan\left(\measuredangle MAC\right)=0{,}625$ | $\tan^{-1}$
$\measuredangle MAC\approx32{,}01^\circ$
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Punkte $P_{n}$ liegen auf der Strecke $[D S]$ . Die Winkel $\angle DAP_n$ haben das Maß $\varphi$ mit $\varphi\in\rbrack\;0^\circ;\;62{,}10^\circ\lbrack$ .
Zeichnen Sie den Punkt $P_{1}$ und die Strecke $[A P_{1}]$ für $\varphi=40°$ in das Schrägbild zur Pyramide in der Aufgabenstellung ein.

Zeichnung des Punktes $P_{1}$ mit
$\measuredangle MAP_1=\varphi=40^\circ$ :
Trage einen $40^\circ$ -Winkel an Punkt A ab (siehe Abbildung rot).
Der Schnittpunkt mit der Höhe [DS] ist der Punkt $P_{1}$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Durch die Punkte $P_{n}$ verlaufen zur Grundfläche $A B C$ parallele Ebenen, die die Kanten der Pyramide $A B C S$ in Punkten $E_n\in\lbrack AS\rbrack$ , $F_n\in\lbrack BS\rbrack$ und $G_n\in\lbrack CS\rbrack$ und die Strecke $[M S]$ in Punkten $N_{n}$ schneiden. Die Dreiecke $E_{n} F_{n} G_{n}$ sind die Grundflächen von Pyramiden $E_{n} F_{n} G_{n} D$ mit der Spitze $D$ .
Zeichnen Sie die Pyramide $E_{1} F_{1} G_{1} D$ und den Punkt $N_{1}$ in das Schrägbild zur Pyramide in der Aufgabenstellung ein.
Zeichnung der Pyramide $E_{1} F_{1} G_{1} D$ :
Zeichne eine Parallele durch den Punkt $P_{1}$ zu [AM] (rot).
Die Parallele schneidet [AS] in Punkt $E_{1}$ und [MS] in Punkt $N_{1}$ .
Konstruiere dann einen $45^\circ$ -Winkel in $N_{1}$ (blau)
(Alternativ: eine Parallele durch $N_{1}$ zu [BC].)
Die Parallele schneidet [CS] in $G_{1}$ und [BS] in $F_{1}$ (nächste Abbildung).
Verbinde nun alle Eckpunkte miteinander (inklusive der Spitze D).
Hast du eine Frage oder Feedback?
Kommentiere hier 👉

Berechnen Sie die Längen der Strecken $[D P_{n}]$ und $[E_{n} N_{n}]$ in Abhängigkeit von $\varphi$ .

[Ergebnisse: $\overline{DP_n}(\varphi)=4{,}5\cdot\tan\left(\varphi\right)\ \text{cm};\;\overline{E_nN_n}(\varphi)=(8-4{,}24\cdot\tan\left(\varphi\right))\ \text{cm}$ ].

Länge der Strecke [ $D P_{n}$ ] in Abhängigkeit von $\varphi$ im rechtwinkligen Dreieck $A D P_{1}$ mithilfe der Trigonometrie:

$\tan\left(\measuredangle DAP_1\right)=\frac{Gegenkathete}{Ankathete}=\frac{\overline{DP_1}}{\overline{AD}}$

$\tan\ \varphi=\dfrac{\overline{DP_1}}{4{,}5\;\text{cm}}$ | $\cdot 4{,}5\;\text{cm}$

$\overline{DP_1}\left(\varphi\right)=\tan\varphi\cdot4{,}5\;\text{cm}$

$\overline{DP_1}\left(\varphi\right)=4{,}5\cdot\tan\varphi\;\text{cm}$

Länge der Strecke [ $E_{n} N_{n}$ ] in Abhängigkeit von $\varphi$ mithilfe des Strahlensatzes (Vierstreckensatz):

$\dfrac{\overline{DS}}{\overline{P_{1}S}}=\dfrac{\overline{AM}}{\overline{E_nN_n}}$

(mit $\overline{P_1S}=\overline{DS}-\overline{DP_n}$ )

$\displaystyle \frac{8{,}5}{8{,}5-4{,}5\cdot\tan\varphi}$	$=$	$\displaystyle \frac{8}{\overline{E_nN_n}}$
	↓	Löse nach $\overline{E_nN_n}$ auf.
$\displaystyle \frac{8{,}5}{8{,}5-4{,}5\cdot\tan\varphi}$	$=$	$\displaystyle \frac{8}{\overline{E_nN_n}}$	$\displaystyle \cdot\overline{E_nP_n}$
$\displaystyle \frac{8{,}5\cdot\overline{E_nN_n}}{8{,}5-4{,}5\cdot\tan\varphi}$	$=$	$\displaystyle 8$	$\displaystyle \cdot(8{,}5-4{,}5\cdot\tan\varphi)$
$\displaystyle 8{,}5\cdot\overline{E_nP_n}$	$=$	$\displaystyle 8\cdot\left(8{,}5-4{,}5\cdot\tan\varphi\right)$	$\displaystyle :8{,}5$
$\displaystyle \overline{E_nN_n}\left(\varphi\right)$	$=$	$\displaystyle \frac{8\cdot8{,}5-8\cdot4{,}5\cdot\tan\varphi}{8{,}5}$
	$=$	$\displaystyle 8-\frac{72}{17}\cdot\tan\varphi$
	$=$	$\displaystyle 8-4{,}24\cdot\tan\varphi$

Ergebnis:

$\overline{E_nN_n}\left(\varphi\right)\approx\left(8-4{,}24\cdot\tan\varphi\ \right)\;\text{cm}$

Hast du eine Frage oder Feedback?

Kommentiere hier 👉

Berechnen Sie das Volumen der Pyramide $E_{1} F_{1} G_{1} D$ .
Volumen der Pyramide $E_{1} F_{1} G_{1} D$ mit:
allgemeine Formel: $V=\frac{1}{3}\cdot G\cdot h$
Die Höhe $h$ berechnen wir wie folgt:
$h=\overline{DP_1}\left(40^\circ\right)=4{,}5\cdot\tan\left(40^\circ\right)cm\approx3{,}78\;\text{cm}$
Die Grundfläche berechnen wir mit folgender Formel: $G=\frac{1}{2}\cdot\overline{E_1N_1}\cdot\overline{F_1G_1}$
$\overline{E_1N_1}=\left(8-4{,}24\cdot\tan\varphi\ \right)\;\text{cm}=\left(8-4{,}24\cdot\tan\left(40^\circ\right)\right)\;\text{cm}\approx4{,}44\;\text{cm}$
$\overline{F_1G_1}=2\cdot\overline{N_1G_1}\$ (rot)
$\overline{N_1G_1}\$ können wir mit Hilfe der Trigonometrie im rechtwinkligen Dreieck $E_{n} N_{n} G_{n}$ berechnen:
Wichtig: Wir benötigen einen Winkel, da die Dreiecke $A B C$ und $E_{1} F_{1} G_{1}$ (ebenso: $\triangle AMC$ und $\triangle E_1N_1G_{1}$ ) ähnlich sind, sind ihre Winkel ebenso gleich groß (neongrün):
$\measuredangle MAC=\measuredangle N_1E_1G_1=32{,}01^\circ$
$\tan\left(\measuredangle N_1E_1G_1\right)=\dfrac{\text{Gegenkathete}}{\text{Ankathete}}=\dfrac{\overline{N_1G_1}}{\overline{E_1N_1}}$
$\tan\left(32{,}01^\circ\right)=\dfrac{\overline{N_1G_1}}{4{,}44\ cm}$ | $\cdot4{,}44\;\text{cm}$
$\overline{N_nG_n}=\tan\left(32{,}01°\right)\cdot4{,}44\ cm\approx2{,}78\;\text{cm}$
Damit ist die Seite $\overline{F_1G_1}=2\cdot\overline{N_1G_1}=2\cdot2{,}78\;\text{cm}\approx5{,}55\;\text{cm}$
Einsetzen in die Volumenformel:
$V=\frac{1}{3}\cdot G\cdot h=\frac{1}{3}\cdot\frac{1}{2}\cdot\overline{E_1N_1}\cdot\overline{F_1G_1}\cdot\overline{DP_1}=\left(\frac{1}{3}\cdot\frac{1}{2}\cdot4{,}44\cdot5{,}55\cdot3{,}78\right)\;\text{cm}^3\approx15{,}52\;\text{cm}^3$
Hast du eine Frage oder Feedback?
Kommentiere hier 👉

3
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
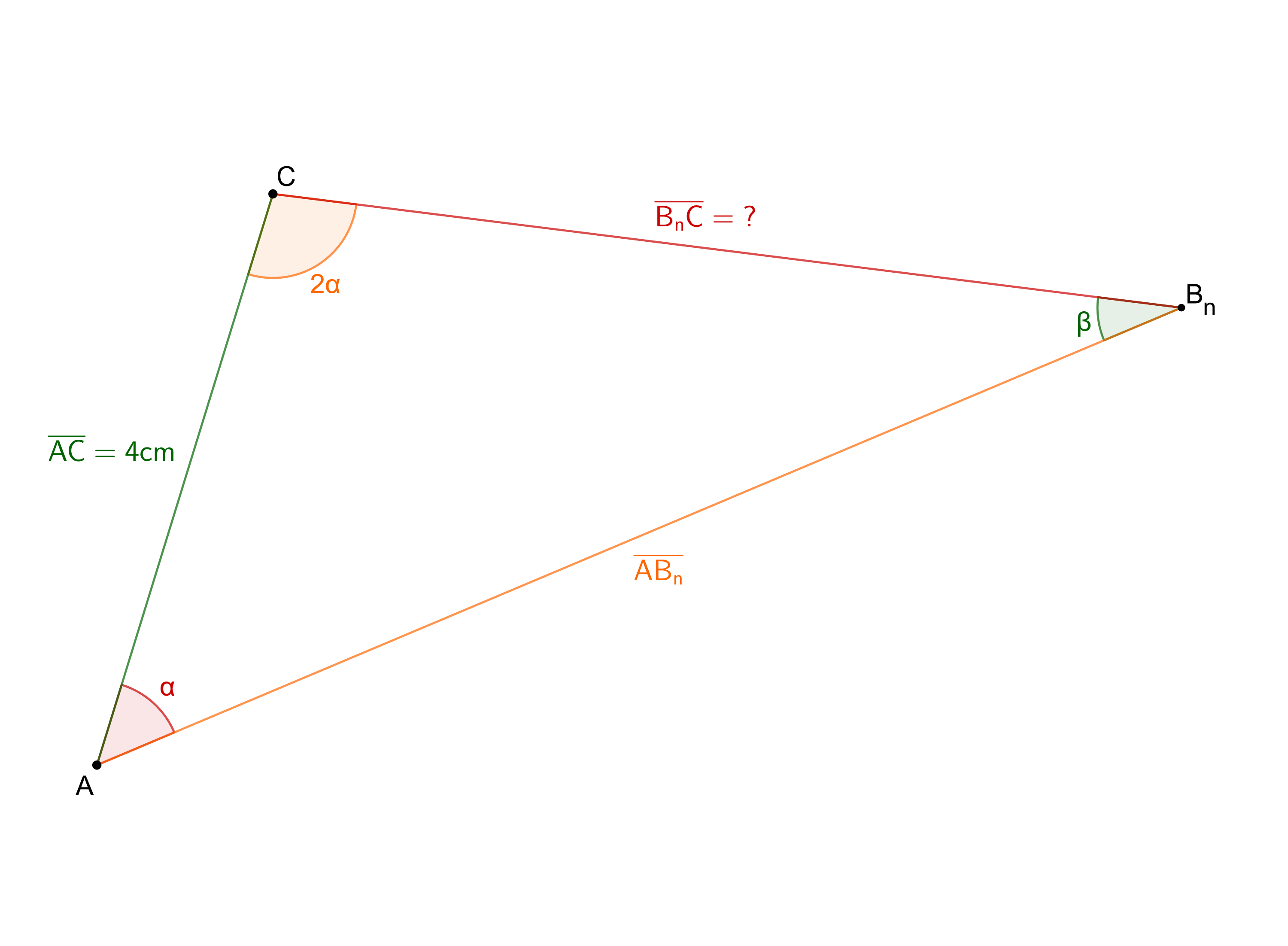
Gegeben sind Dreiecke $A B_{n} C$ mit der Seitenlänge $\overline{AC}=4\ \text{cm}$ . Die Winkel $B_{n} A C$ haben das Maß $\alpha$ mit $\alpha\in\rbrack0^\circ;\;60^\circ\lbrack$ . Das Maß der Winkel $A C B_{n}$ ist doppelt so groß wie das Maß der Winkel $B_{n} A C$ .
1. Ergänzen Sie die Zeichnung zum Dreieck $A B_{1} C$ für $\alpha=50^\circ$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Sinussatz und Kosinussatz im allgemeinen Dreieck
  Skizziere das Dreieck für $\alpha = 50°$ .
  Du sollst ein Dreieck $\Delta AB_1C$ zeichnen, wobei die Strecke $\overline{AC}$ $4\;\text{cm}$ lang und der Winkel $\measuredangle B_1AC=\alpha=50°$ und der Winkel $\measuredangle ACB_1=2\alpha=2\cdot50^{\circ}=100°$ groß sind. Das folgende Applet zeigt dir, wie du das machen kannst.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
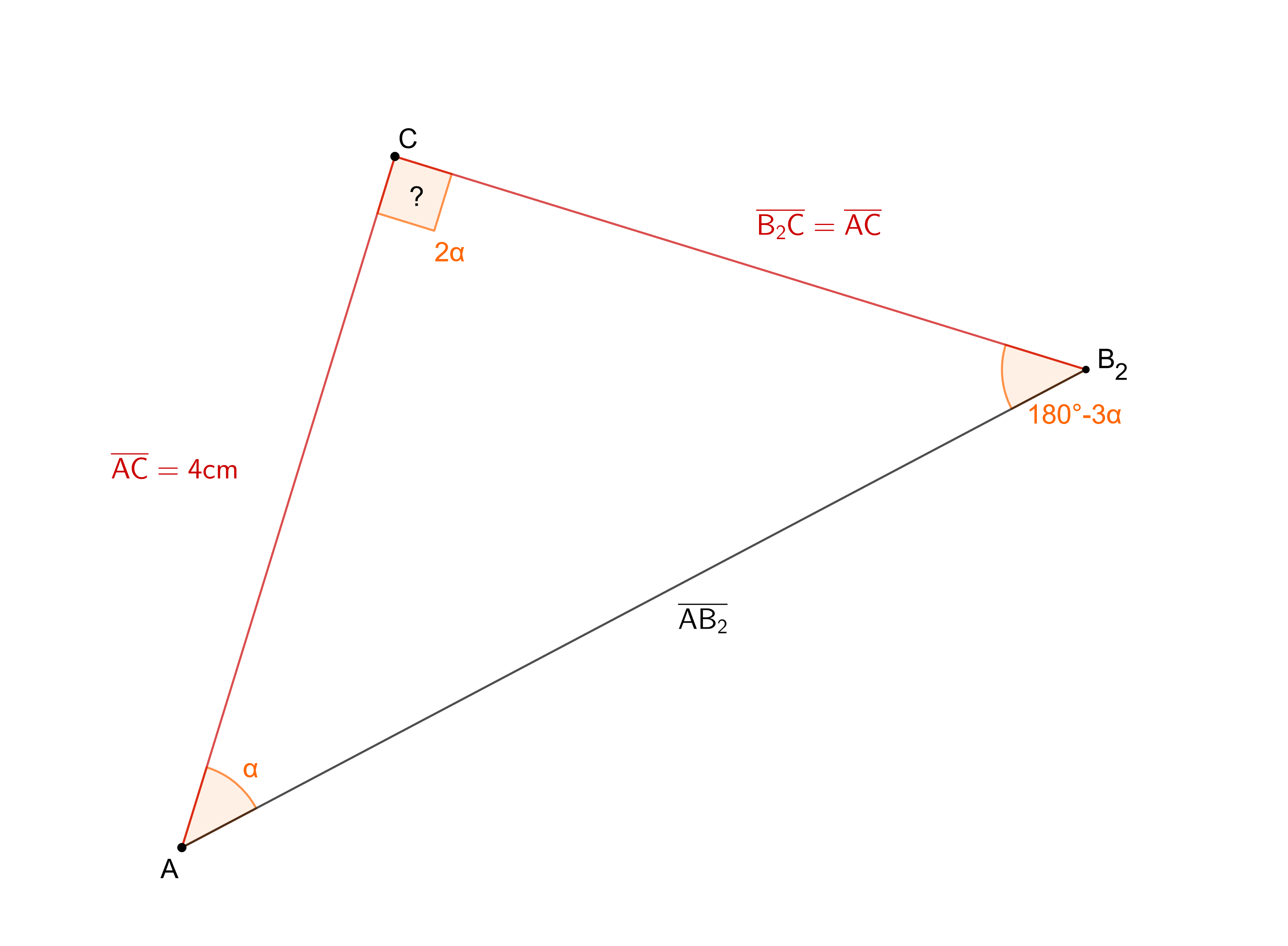
2. Bestimmen Sie die Länge der Strecken $[B_{n} C]$ in Abhängigkeit von $\alpha$ und vereinfachen Sie mithilfe einer Supplementbeziehung.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Sinussatz und Kosinussatz im allgemeinen Dreieck
  Finde eine Formel für $\overline{B_nC}$ .
  Um eine Formel für die Länge der Strecke $\overline{B_nC}$ zu finden, schau dir zunächst das Dreieck an, wie du es bisher kennst:
  Du kennst die Strecke $\overline{AC}$ und sollst den Winkel $\alpha$ für die Lösung verwenden. Weil das Dreieck nicht rechtwinklig ist, kommt nur der Sinussatz in Frage.
  Der Sinussatz sagt, dass das Verhältnis des Sinus jeden Winkels und der Länge der gegenüberliegenden Strecke gleich ist:
  $\displaystyle \color{red}\frac{\overline{B_nC}}{\sin(\alpha)}\color{b}=\color{green}\frac{\overline{AC}}{\sin(\beta)}\color{b}=\color{orange}\frac{\overline{AB_n}}{\sin(2\alpha)}.$
  Zwei der Winkel sind mit $\alpha$ und $2\alpha$ gegeben, $\beta$ ergibt sich nach der Winkelsumme im Dreieck von $180^\circ$ zu
  $\displaystyle \beta=180^\circ-\measuredangle B_nAC-\measuredangle ACB_n=180^\circ-\alpha-2\alpha=180^\circ-3\alpha$
  Die Winkel kannst du in deiner Lösung alle verwenden. Der dritte Term interessiert nicht, weil $\overline{AB_n}$ weder gesucht, noch gegeben ist. Du kannst die Formel nach $\overline{B_nC}$ umstellen:
  $\displaystyle \def\arraystretch{2} \begin{array}{c}&\dfrac{\overline{B_nC}}{\sin{(\alpha)}}&=&\dfrac{\overline{AC}}{\sin{(180^\circ-3\alpha)}}&\quad|\cdot\sin{(\alpha)}\\\\\Leftrightarrow&\overline{B_nC}&=&\overline{AC}\cdot\dfrac{\sin{(\alpha)}}{\sin{(180^\circ-3\alpha)}}&\end{array}$
  Nun kannst du, wie in der Aufgabenstellung verlangt, eine Supplementbeziehung für den Sinus anwenden:
  $\displaystyle \sin{(180^\circ-3\alpha)}=\sin{(3\alpha)}$
  und erhältst damit
  $\displaystyle \overline{B_nC}=\overline{AC}\cdot\dfrac{\sin{(\alpha)}}{\sin{(3\alpha)}}=4\;\text{cm}\cdot\dfrac{\sin{(\alpha)}}{\sin{(3\alpha)}}.$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. Das Dreieck $A B_{2} C$ ist gleichschenklig mit der Basis $[A B_{2}]$ . Begründen Sie, dass das Dreieck $A B_{2} C$ rechtwinklig ist.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Sinussatz und Kosinussatz im allgemeinen Dreieck
  Zeige, dass das Dreieck, wenn es gleichschenklig ist, auch rechtwinklig ist.
  In einem gleichschenkligen Dreieck sind zwei Innenwinkel gleich, nämlich die Winkel zwischen den Schenkeln und der Basis:
  $\displaystyle \measuredangle CB_2A=\measuredangle B_2AC$
  In diesem Dreieck bedeutet das dann, dass
  $\displaystyle \alpha=180^{\circ}-3\alpha$
  gelten muss. Die Formel kannst du umstellen: Addiere zunächst $3\alpha$ auf beiden Seiten.
  $\displaystyle \Leftrightarrow 4\alpha=180^{\circ}$
  und teile dann durch 4:
  $\displaystyle \Leftrightarrow\alpha=45^{\circ}.$
  Nun hast du herausgefunden, dass der Winkel $\alpha \;45^\circ$ groß sein muss, wenn das Dreieck rechtwinklig ist. Es ist in der Aufgabenstellung gegeben, dass $\measuredangle ACB_n=2\alpha=2\cdot45^\circ=90^\circ$ ist, also ist das Dreieck tatsächlich rechtwinklig!
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉