Das Integral stellt einen orientierten Flächeninhalt dar, doch man kann damit auch Flächeninhalte allgemeinerer Flächen, die durch Einschluss verschiedener Funktionsgraphen gegeben sind, berechnen.
Integral als Flächenbilanz
Das Integral wird dazu verwendet, Flächen zwischen den Koordinatenachsen und einem Graphen oder zwischen zwei verschiedenen Graphen zu berechnen. Das Problem ist, dass der Wert des Integrals nur dann mit der tatsächlichen Fläche übereinstimmt, wenn im gewählten Abschnitt der Graph (welcher im Fall der Fläche innerhalb zweier Graphen der Graph der Differenz der dazugehörigen Funktionen ist) oberhalb der x-Achse liegt.
Im Allgemeinen ist das Integral nur die Flächenbilanz, also die Differenz von der Fläche oberhalb der x-Achse und der Fläche unterhalb der x-Achse.
Befinden sich in diesem Bereich eine oder mehrere Nullstellen, so muss man die Funktion in jedem Intervall zwischen zwei benachbarten Nullstellen einzeln betrachten, wenn man die tatsächliche eingeschlossene Fläche herausfinden will.
Die einzelnen Flächen werden dann betragsmäßig addiert; die Maßzahl nicht orientierten Flächeninhalts ist immer positiv.
Ein ausführliches Beispiel findet sich am Ende des Artikels.
Flächenberechnung zwischen x-Achse und Graph von
Der Hauptsatz der Differential- und Integralrechnung (HDI) besagt, dass, falls der Graph der dazugehörigen Fläche die x-Achse nicht schneidet (man beachte dazu den obigen Abschnitt),
gilt, wobei eine beliebige Stammfunktion von ist und und die zwei -Werte sind, welche die Fläche links und rechts begrenzen.
Beispiel
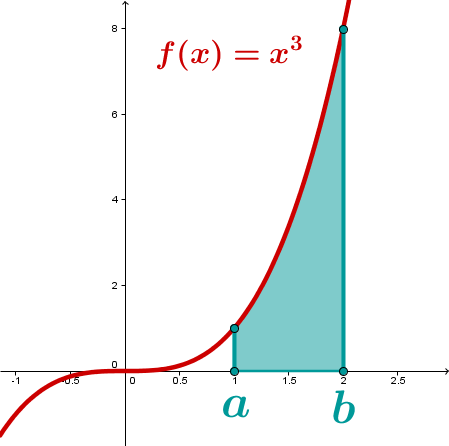
Will man die Fläche zwischen der x-Achse und dem Graphen von mit im Intervall berechnen, so erhält man unter Benutzung der obigen Formel (man beachte, dass der Graph komplett über der x-Achse verläuft)
Flächenberechnung zwischen zwei beliebigen Graphen
Manchmal interessiert man sich für die Fläche, die zwischen zwei benachbarten Schnittpunkten und der zwei Graphen der Funktionen und liegt.
Beispiel
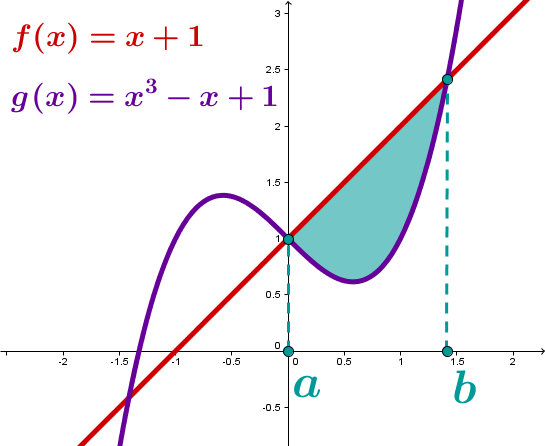
Will man die Fläche zwischen den Graphen der beiden Funktionen und mit und berechnen, so muss man zuerst die beiden Schnittpunkte berechnen; diese sind (wie im Artikel Schnittpunkte zweier Funktionen berechnen beispielhaft berechnet wird) und . Die Grafik im Artikel zeigt, dass im Intervall größer als ist, und sich somit für den Flächeninhalt
ergibt.
Der Flächeninhalt einer Funktion mit Vorzeichenwechsel
Die Problematik, den Flächeninhalt (und nicht die Flächenbilanz) zwischen dem Graphen einer Funktion mit Vorzeichenwechsel und der x-Achse zu berechnen, wurde schon zu Beginn des Artikels angesprochen, deshalb folgt hier ein Beispiel.
Beispiel
Will man die Fläche zwischen dem Graphen der Funktion und der x-Achse zwischen -2 und 2 berechnen, so ist zu beachten, dass punktsymmetrisch zum Ursprung ist; in einem zu null symmetrischen Intervall wie heben sich die Flächen im negativen und im positiven Bereich auf. (siehe Rechenregeln des Integrals)
Um das Maß des Flächeninhalts zu berechnen, sucht man zunächst alle Nullstellen in diesem Bereich:
Da der Graph symmetrisch ist, reicht es aus, die Flächenstücke auf einer Seite der y-Achse zu berechnen und den Wert zu verdoppeln: Die Flächenstücke rechts und links der x-Achse sind also gleich groß.
Fläche unter dem Graphen zwischen 0 und 2
Das Flächenmaß unter dem Graphen zwischen und beträgt also .
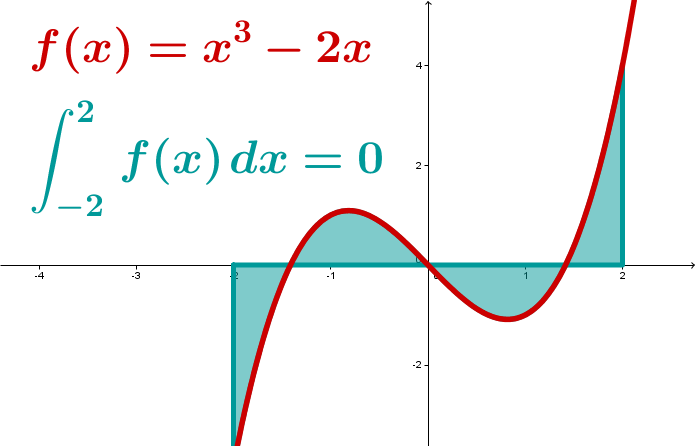
Übungsaufgaben
Laden
Laden
Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:
Aufgaben zu Flächenberechnung mit Integralen
