Aufgaben zu Flächenberechnung mit Integralen
Mit diesen gemischten Übungsaufgaben lernst du das Bestimmen von Flächeninhalten mit Integralen. Schaffst du sie alle?
- 1
Sei die Funktion gegeben. Bestimme die Fläche, die von und ihrer Umkehrfunktion eingeschlossen wird.
- 2
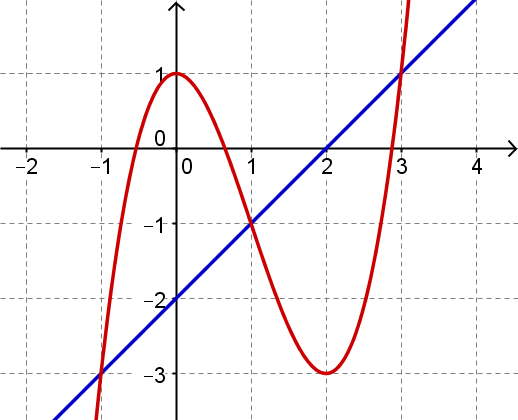
Die beiden abgebildeten Graphen schneiden sich in drei Punkten, die jeweils ganzzahlige Koordinaten besitzen.
Zum "roten Graphen" gehört eine Funktion dritten Grades mit dem Hochpunkt und dem Tiefpunkt .
Bestimme die jeweiligen Funktionsterme und die Schnittpunkte der Graphen.
Wie kannst du den gesamten Inhalt A der von den beiden Graphen eingeschlossenen Fläche mit bestimmten Integralen angeben?
Berechne nun A.
- 3
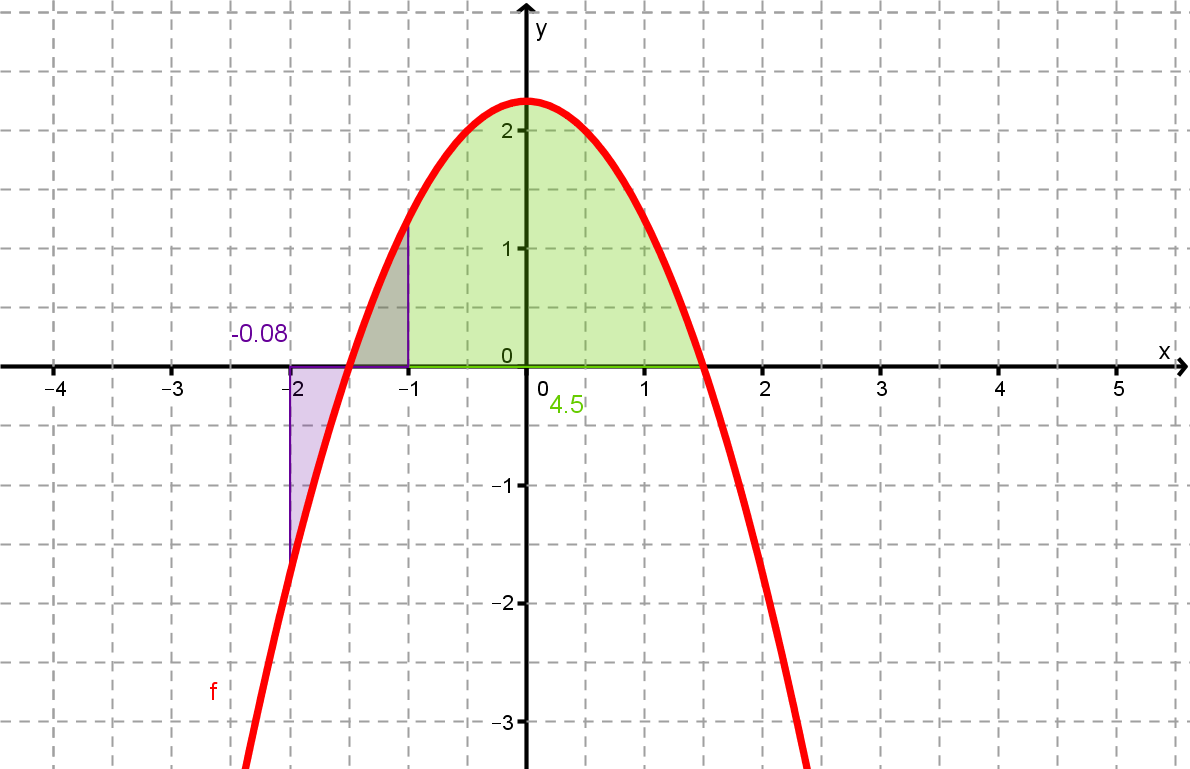
Die Parabel mit dem Scheitel und der Graph der Funktion f mit schließen eine Fläche mit dem Inhalt A ein.
Bestimme den zur Parabel gehörenden Funktionsterm und alle Schnittpunkte.
Wie kannst du A als bestimmtes Integral schreiben? Berechne nun A.
- 4
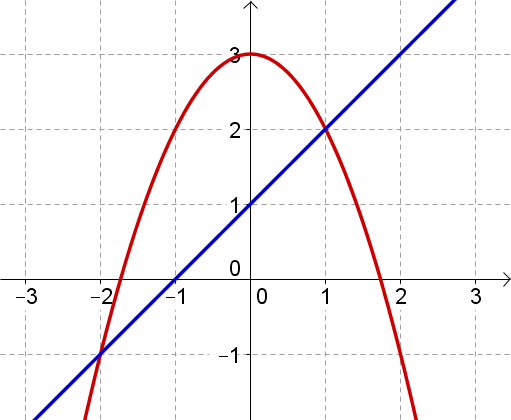
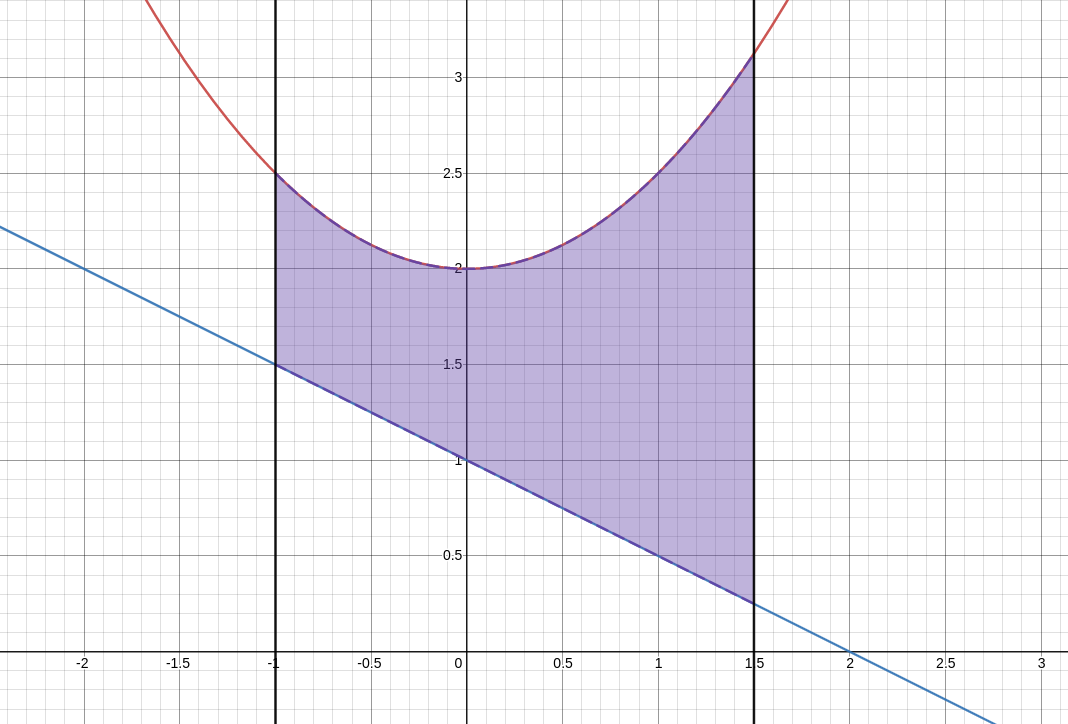
Die abgebildete Parabel und Gerade schließen eine Fläche mit dem Inhalt ein.
Schraffiere diese Fläche.
Bestimme die Funktionsterme von und und die beiden Schnittpunkte und der Graphen.
Gib als bestimmtes Integral an und berechne dann .
- 5
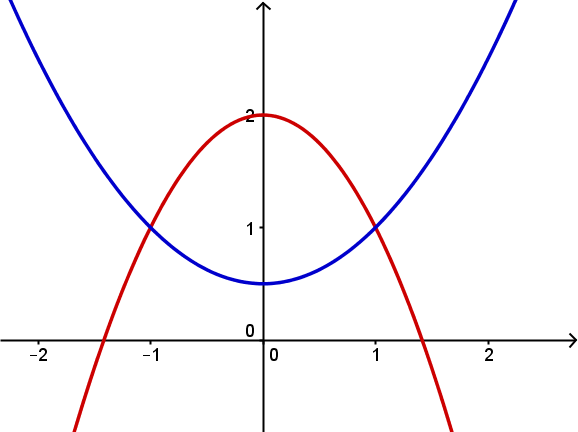
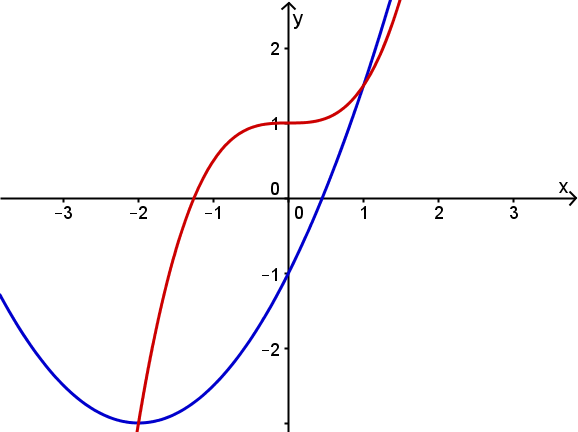
Die Graphen der Funktionen und schließen eine Fläche mit dem Inhalt A ein.
Schraffiere diese Fläche und berechne A.
- 6
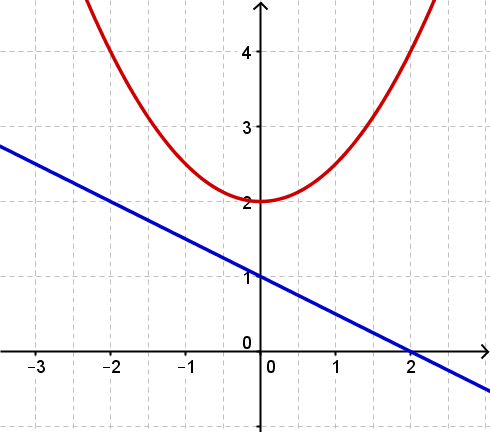
Das Bild zeigt die Graphen der beiden Funktionen und .
Man erkennt: für alle .
Berechne den Inhalt A der Fläche zwischen den beiden Graphen und den Grenzen und .
Zeichne diese Fläche ein.
- 7
Berechne den Inhalt des Flächenstücks, das und die x-Achse einschließen.
- 8
Berechne den Inhalt der Fläche, die zwischen der x-Achse und liegt.
- 9
Bestimme die Gleichung der Ursprungsgeraden, die im Hochpunkt schneidet, und berechne den Inhalt der Fläche, die von und der Geraden eingeschlossen ist.
- 10
Bestimme die Fläche zwischen den Graphen der Funktionen.
;
;
- 11
Berechne den Inhalt des Flächenstücks zwischen und der x-Achse.
- 12
Berechne die zwischen und der -Achse eingeschlossene Fläche für die folgenden Funktionen :
- 13
Berechne ; ;
Berechne den Inhalt des Flächenstücks zwischen , der y-Achse und der Geraden im Bereich von bis
- 14
Gegeben ist der Graph einer integrierbaren Funktion .
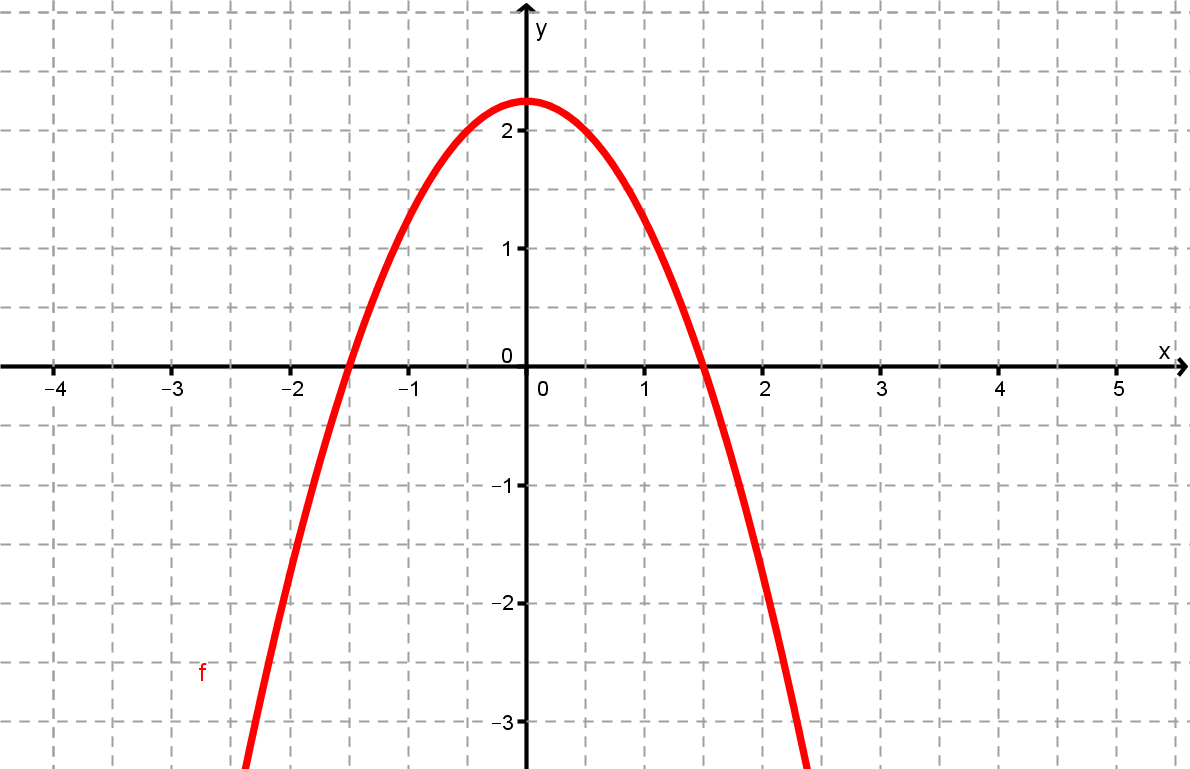
Bestimme graphisch näherungsweise den Flächeninhalt, den die Funktion mit der x-Achse einschließt.
Gib näherungsweise zwei Nullstellen der Integralfunktion
an.
- 15
Das stilisierte Fischlogo des Marineclubs soll neu lackiert werden. Dazu braucht der Maler die Fläche des Logos.
Die orangefarbene Randfunktion ist gegeben durch .
Fischlogo
- 16
Gegeben sind die beiden Funktionen und mit .
Berechne das Flächenstück oberhalb der x-Achse, das von den Graphen der beiden Funktionen und begrenzt wird.
Wie groß ist der eingeschlossene Flächeninhalt, wenn ist?
- 17
Gegeben sind die Funktionen
und
mit . Die beiden Funktionsgraphen und die senkrechte Gerade schließen im ersten Quadranten eine Fläche ein, die aus zwei Teilflächen besteht. Skizzieren Sie den Sachverhalt und bestimmen Sie m so, dass die beiden Teilflächen die gleichen Flächeninhalte besitzen.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?