Pflichtteil - lernen mit Serlo!

Funktionskompetenz

Die Abbildung zeigt das Schaubild der Ableitung $f^{'}$ einer Funktion $f$ . Begründen Sie, ob folgende Aussagen über die Funktion $f$ wahr, falsch oder unentscheidbar sind.
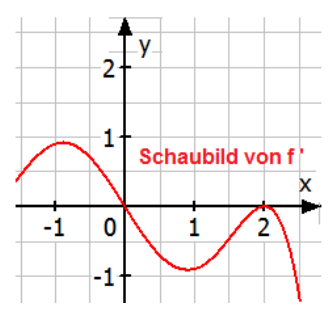
a) An der Stelle $0$ hat das Schaubild von $f$ einen Hochpunkt.
b) Für $0 \leq x \leq 2$ ist $f (x) \leq 0$ .
c) Das Schaubild von $f$ ist punktsymmetrisch zum Ursprung für $- 1 < x < 1$ .
d) An der Stelle $2$ hat das Schaubild von $f$ einen Wendepunkt.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Kurvendiskussion
Lösung zu a)
An der Stelle $x = 0$ ist $f^{'} (x) = 0$ und $f^{'} (x)$ hat hier einen Vorzeichenwechsel von $+$ nach $-$ . Das Schaubild von $f (x)$ hat somit bei $x = 0$ einen Hochpunkt.
Die Aussage ist wahr.
Lösung zu b)
Der Verlauf von $f^{'} (x)$ lässt keine eindeutigen Rückschlüsse auf den Verlauf von $f (x)$ zu.
Die Aussage ist unentscheidbar.
Lösung zu c)
Für $- 1 < x < 1$ entnimmst du dem Schaubild, dass hier $f^{'} (x)$ punktsymmetrisch zum Ursprung ist. Demnach muss Schaubild von $f (x)$ achsensymmetrisch zur y-Achse sein.
Die Aussage ist falsch.
Lösung zu d)
An der Stelle $x = 2$ ist $f^{'} (x)$ maximal, d.h. $f^{''} (x) = 0$ . Außerdem ist $f^{'} (2) = 0$ und $f^{'} (x)$ hat hier keinen Vorzeichenwechsel, sodass hier ein Terrassenpunkt oder Sattelpunkt vorliegt.
Die Aussage ist wahr.
(Anmerkung: Ein Terrassenpunkt oder Sattelpunkt ist ein Wendepunkt, in dem die Steigung einer Funktion 0 wird.)
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
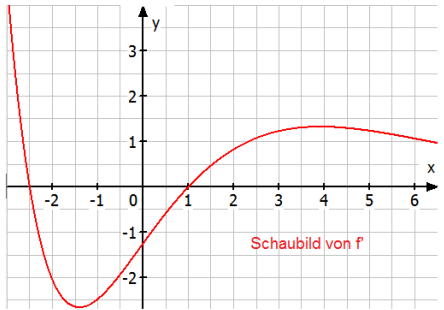
Die Abbildung zeigt das Schaubild der Ableitung $f^{'}$ einer Funktion $f$ .
a) Begründen Sie, welche Aussagen man in dem dargestellten Bereich hinsichtlich der Anzahl der
- Extremstellen,
- Wendestellen
und Nullstellen
von $f$ man treffen kann.
b) Begründen Sie, dass $\int_{- 2}^{3} f^{'} (x) d x < 0$ gilt.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Kurvendiskussion
Lösung zu a)
Anzahl der Extremstellen: Der Abbildung entnimmst du, dass $f^{'} (x)$ zwei Nullstellen jeweils mit Vorzeichenwechsel hat. Demnach hat $f (x)$ zwei Extrema.
Anzahl der Wendestellen: Der Abbildung entnimmst du, dass $f^{'} (x)$ zwei Extrema hat. Hier ist jeweils $f^{''} (x) = 0$ . Demnach hat $f (x)$ zwei Wendestellen.
Anzahl der Nullstellen: Sowohl die Ableitung von $f (x)$ als auch die Ableitung von $f (x) + c$ (Graph von $f (x)$ parallel zur y-Achse verschoben) ergeben die gleiche Ableitungsfunktion $f^{'} (x)$ . Somit ist keine genaue Aussage über die Anzahl der Nullstellen von $f (x)$ möglich.
Allerdings weißt du, dass zwischen zwei Nullstellen von $f$ immer ein Extremum liegen muss. Daher kann $f$ höchstens drei Nullstellen haben.
Lösung zu b)
Das Integral $\int_{- 2}^{3} f^{'} (x) d x$ kann in zwei Teile zerlegt werden: $\int_{- 2}^{3} f^{'} (x) d x = \int_{- 2}^{1} f^{'} (x) d x + \int_{1}^{3} f^{'} (x) d x$
Dabei gilt: $| \int_{- 2}^{1} f^{'} (x) d x | > \int_{1}^{3} f^{'} (x) d x$ . Der Wert des Integrals $\int_{- 2}^{1} f^{'} (x) d x$ ist negativ, da die Fläche unter der $x$ -Achse liegt. Insgesamt ist dann die Flächenbilanz negativ, sodass die angegebene Ungleichung stimmt.
Du kannst auch z.B. durch das Zählen von ganzen Kästchen feststellen, dass schon $\int_{- 2}^{- 1 / 2} f (x) d x < - 3$ und $\int_{1}^{3} f (x) d x < 3$ ist.
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Die Abbildung zeigt das Schaubild der Ableitung $f^{'}$ einer Funktion $f$ .
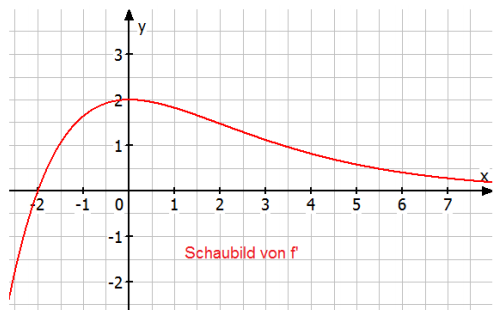
Begründen Sie, ob folgende Aussagen über die Funktion $f$ wahr, falsch oder unentscheidbar sind.
a) Bei $x = 0$ besitzt das Schaubild von $f$ einen Extrempunkt.
b) Bei $x = - 2$ besitzt das Schaubild von f eine waagrechte Tangente.
c) Das Schaubild der Funktion $f$ besitzt keine Wendepunkte.
d) $f (x) > 0$ für $x > - 2$ .

Für diese Aufgabe benötigst Du folgendes Grundwissen: Kurvendiskussion
Lösung zu a)
An der Stelle $x = 0$ ist $f^{'} (0) = 2$ , d.h. die Steigung ist hier positiv. Bei einem Extrempunkt müsste die Steigung aber $0$ sein.
Die Aussage ist falsch.
Lösung zu b)
$f^{'} (- 2) = 0$ und $f^{'} (x)$ hat hier einen Vorzeichenwechsel, sodass hier eine Extremstelle mit waagrechter Tangente vorliegt.
Die Aussage ist wahr.
Lösung zu c)
An der Stelle $x = 0$ ist $f^{''} (0) = 0$ , d.h. der Graph hat hier einen Wendepunkt.
Die Aussage ist falsch.
Lösung zu d)
Sowohl die Ableitung von $f (x)$ als auch die Ableitung von $f (x) + c$ (Graph von $f (x)$ parallel zur y-Achse verschoben) ergeben die gleiche Ableitungsfunktion $f^{'} (x)$ . Aus dem Verlauf von $f^{'} (x)$ kann nicht auf den Verlauf von $f (x)$ rückgeschlossen werden.
Die Aussage unentscheidbar.
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Gegeben sind die Schaubilder zweier Funktionen $f$ und $g .$ Eine der beiden Funktionen ist die Ableitungsfunktion der anderen Funktion.
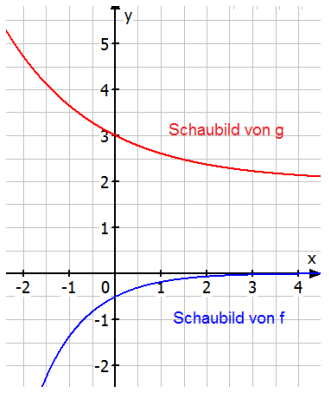
a) Begründen Sie, dass die Funktion $f$ die Ableitung der Funktion $g$ ist.
b) Die Funktion $g$ hat die Funktionsgleichung $g (x) = e^{a x} + b$ . Bestimmen Sie $a$ und $b .$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Kurvendiskussion
Lösung zu a)
Für $x > 0$ ist die Steigung der Funktion $f (x)$ kleiner als $1$ . Da aber $g (x)$ für $x >$ 0 immer $> 2$ ist, kann $g (x)$ nicht die Ableitungsfunktion von $f (x)$ sein. Demnach ist $g^{'} (x) = f (x)$ .
Antwort: Die Funktion $f (x)$ ist die Ableitung der Funktion $g (x)$ .
Lösung zu b)
Es gilt: $g (0) = 3$ $\Rightarrow 3 = e^{0} + b \Rightarrow 3 = 1 + b \Rightarrow b = 2$
$y_{A} = 2$ ist auch die waagrechte Asymptote der Funktion $g (x)$ .
Somit ist $g (x) = e^{a x} + 2 \Rightarrow g^{'} (x) = a \cdot e^{a x} = f (x)$ wie in Aufgabe a) nachgewiesen.
$f (0) = - \frac{1}{2} \Rightarrow g^{'} (0) = - \frac{1}{2} = a \cdot e^{0} = a$
Antwort: $a = - \frac{1}{2}$ und $b = 2$ . Damit folgt für die Funktion $g (x) = e^{- \frac{1}{2} \cdot x} + 2$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Die 4 Abbildungen zeigen die Schaubilder von Funktionen. Eines dieser Schaubilder gehört zu der Funktion $f$ mit $f (x) = \frac{a}{1 + x^{2}} - 1$ .
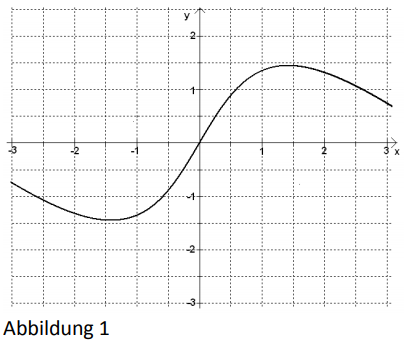
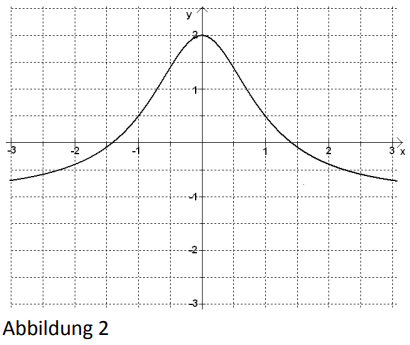
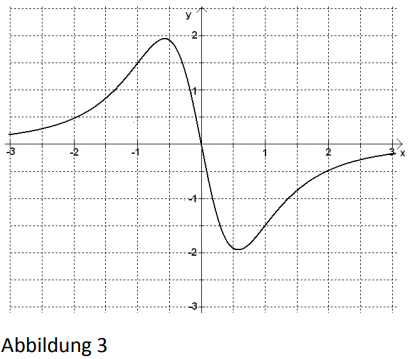
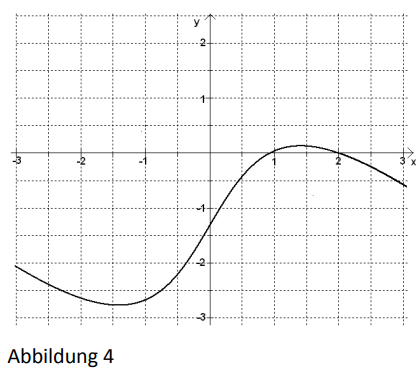
a) Begründen Sie, dass Abbildung 2 zur Funktion $f$ gehört. Bestimmen Sie den Wert von a.
b) Von den anderen drei Abbildungen gehört eine zur Ableitungsfunktion $f^{'}$ und eine zur Integralfunktion $I$ mit $I (x) = \int_{2}^{x} f (t) d t$ . Ordnen Sie diesen beiden Funktionen die zugehörigen Abbildungen zu und begründen Sie jeweils Ihre Zuordnung.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Kurvendiskussion
Lösung zu a)
Die gegebene Funktion $f (x) = \frac{a}{1 + x^{2}} - 1$ ist wegen $f (- x) = f (x)$ achsensymmetrisch zur y-Achse. Die Abbildung $2$ ist die einzige Funktion, die achsensymmetrisch zur y-Achse ist. Außerdem hat $f (x)$ eine waagrechte Asymptote $y_{A} = - 1$ und nur der Graph in Abbildung $2$ hat auch eine waagrechte Asymptote $y_{A} = - 1$ .
Es gilt: $f (0) = 2 \Rightarrow 2 = \frac{a}{1 + 0} - 1 \Rightarrow a = 3$
Antwort: Abbildung $2$ gehört zur Funktion $f (x)$ und $a$ hat den Wert $3$ .
Lösung zu b)
Der Graph der Funktion $f (x) = \frac{3}{1 + x^{2}} - 1$ hat bei $x = 0$ einen Hochpunkt $\Rightarrow f^{'} (0) = 0$ mit Vorzeichenwechsel von $+$ nach $-$ . Nur Abbildung $3$ erfüllt diese beiden Bedingungen.
Die Integralfunktion $I (x) = \int_{2}^{x} f (t) d t$ hat für $x = 2$ eine Nullstelle. Nur die Abbildung $4$ hat bei $x = 2$ eine Nullstelle.
Antwort: Abbildung $3$ gehört zur Ableitungsfunktion $f^{'} (x)$ und Abbildung $4$ gehört zur Integralfunktion $I (x)$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👇