Die Zufallsgröße kann die Werte 0, 1, 2, 3 und 4 annehmen. Die Tabelle zeigt die Wahrscheinlichkeitsverteilung von Y mit .
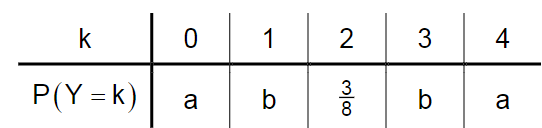
a) Beschreiben Sie, woran man unmittelbar erkennen kann, dass der Erwartungswert von gleich 2 ist .
Die Varianz von ist gleich .
b) Bestimmen Sie die Werte von und .
c) Die Zufallsgröße , die für eine Laplace-Münze die Anzahl des Auftretens von „Zahl“ bei viermaligem Werfen beschreibt, hat ebenfalls den Erwartungswert 2 und es gilt analog . Berechnen Sie die Varianz von , vergleichen Sie diese mit der Varianz von und beschreiben Sie davon ausgehend einen qualitativen Unterschied der Wahrscheinlichkeitsverteilungen von und .
