3Exkurs: Herleitung über Flächen von Quadraten
Auf den letzten Seiten hast du kennengelernt, wie man die binomischen Formeln durch Ausmultiplizieren herleitet. Es gibt aber noch die Möglichkeit, die Formeln durch Flächenvergleiche herzuleiten. Für die erste binomische Formel funktioniert das so:
Berechnet man den Flächeninhalt des gesamten Quadrats, dann bekommt man mit Seitenlänge als Ergebnis .
Zählt man stattdessen die Flächeninhalte der vier Vierecke zusammen, so bekommt man .
Bei diesen zwei unterschiedlichen Herangehensweisen kommen wir auf dasselbe Ergebnis, also gilt .
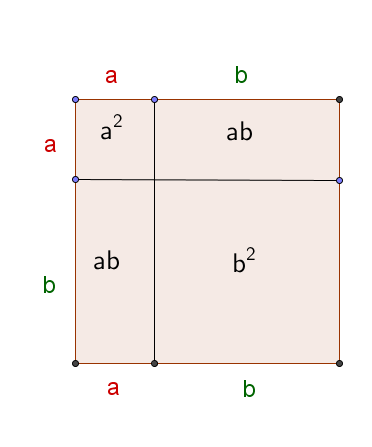
Die grafischen Herleitungen der anderen beiden Formeln kannst du im Artikel Binomische Formeln nachlesen.
