Winkel konstruieren

Direkt konstruierbare Winkel

Folgende Winkel können direkt konstruiert werden:

• $360^\circ$ (Vollwinkel)

• $180^\circ$ (gestreckter Winkel)

• $90^\circ$ (rechter Winkel)

• $60^\circ$

• $0^\circ$

Konstruktion eines $90^\circ$ Winkels

Man konstruiert einen $90^\circ$ Winkel (rechter Winkel), indem man ein Lot auf einer Geraden fällt.

Konstruktion eines $60^\circ$ Winkels

1. Zeichne einen Kreis um den Punkt $A$ mit dem Radius $r$.

2. Zeichne einen weiteren Kreis um den Schnittpunkt des ersten Kreises mit der Geraden mit demselben Radius r.

3. Der Schnittpunk der beiden Kreise ist ein Punkt auf dem zweiten Schenkel des $60^\circ$ Winkels.

Interessantes:

Die Idee bei der Konstruktion eines $60^\circ$ Winkels ist die Konstruktion eines gleichseitigen Dreiecks, da jeder Innenwinkel davon $60^\circ$ beträgt.

Zusammengesetzte Winkel konstruieren

Folgende Winkel sind auch konstruierbar:

• Winkel, die sich als Summe aus direkt konstruierbaren Winkel zusammen setzten lassen.

  Beispiel

• $120^\circ=60^\circ+60^\circ$

• $150^\circ=90^\circ+60^\circ$

• Winkel, die sich durch (wiederholtes) halbieren von direkt konstruierbaren Winkel ergeben.

  Beispiel

• $45^{\circ}=\frac{1}{2}\cdot90^{\circ}$

• $30^\circ=\frac12\cdot60^\circ$

• $15^{\circ}=\frac{1}{2}\cdot\frac{1}{2}\cdot60^{\circ}=\frac{1}{2}\cdot30^{\circ}$

• Winkel, die sich durch Summation, Subtraktion und halbieren von bereits konstruierten Winkel ergeben.

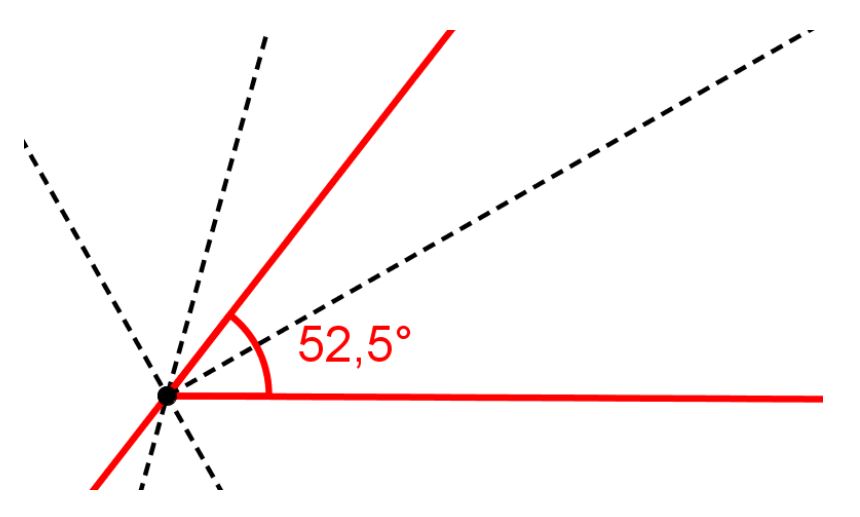
  Beispiel

• $135^{\circ}=90^{\circ}+45^{\circ}=90^{\circ}+\frac{1}{2}\cdot90^{\circ}$

• $75^{\circ}=45^{\circ}+30^{\circ}=\frac{1}{2}\cdot90^{\circ}+\frac{1}{2}\cdot60^{\circ}$

Addition von Winkel

1. Konstruiere einen weiteren Winkel an einem Schenkel des schon vorhandenen Winkels.

2. Der neue Winkel geht vom anderen Schenkel bis zum dazu konstruierten Winkel.

Subtraktion von Winkel

1. Konstruiere einen Winkel an einem Schenkel, wobei der neue Winkel zwischen den alten Schenkeln liegt. (Im Applet wird von einem $90^\circ$ Winkel ein $60^\circ$ Winkel abgezogen, sodass ein $30^\circ$ Winkel entsteht.)

2. Der neue Winkel ist der Teil des ursprünglichen Winkels, der nicht von dem neu konstruierten Winkel überdeckt wird.

Halbieren von Winkeln

Man halbiert einen Winkel, indem man die Winkelhalbierende konstruiert.