Direkte und indirekte Proportionalität

Kurs

1 Übersicht

In diesem Kurs lernst du, was sich hinter den Begriffen direkte und indirekte Proportionalität versteckt - und dass das gar nicht so gruselig oder schwer ist, wie es klingt!

Nützliches Vorwissen:

Wertetabellen zeichnen und Termwerte berechnen
Zuordnungen aufstellen und verstehen
Geraden und Hyperbeln zeichnen und Funktionsgleichungen bestimmen

danach kannst du:

Erklären, was sich hinter den Begriffen direkte/indirekte Proportionalität, Produktgleichheit, Quotientengleichheit und Proportionalitätsfaktor verbirgt
Entscheiden, ob zwei Größen direkt oder indirekt proportional zueinander sind
Fehlende Angaben proportionaler Größen berechnen
Graphen von Funktionen zeichnen, die proportionale Zusammenhänge darstellen

Kursdauer: 45-90 Minuten

2 Ein Einkaufswagen voller Melonen

Du bist bei Alexander zu Hause. Alexander ist einer der Personen, die in Mathebüchern vorkommt, weil er sich 60 Melonen kauft oder zum Spaß 30 Badewannen mit Reiskörnern vollfüllt.

Als du ihn fragst, warum er das tut, antwortet er: "Na für die Mathematik! Hier konkret, um die Schönheit der proportionalen Zusammenhänge zu zeigen."

Du schiebst eine Melone neben dir zur Seite, um bequemer auf dem Sofa sitzen zu können und fragst nach: "Proportionale Zusammenhänge? Was ist das?"

"Es ist ganz einfach, ich erkläre es dir!"

3 Proportionalität

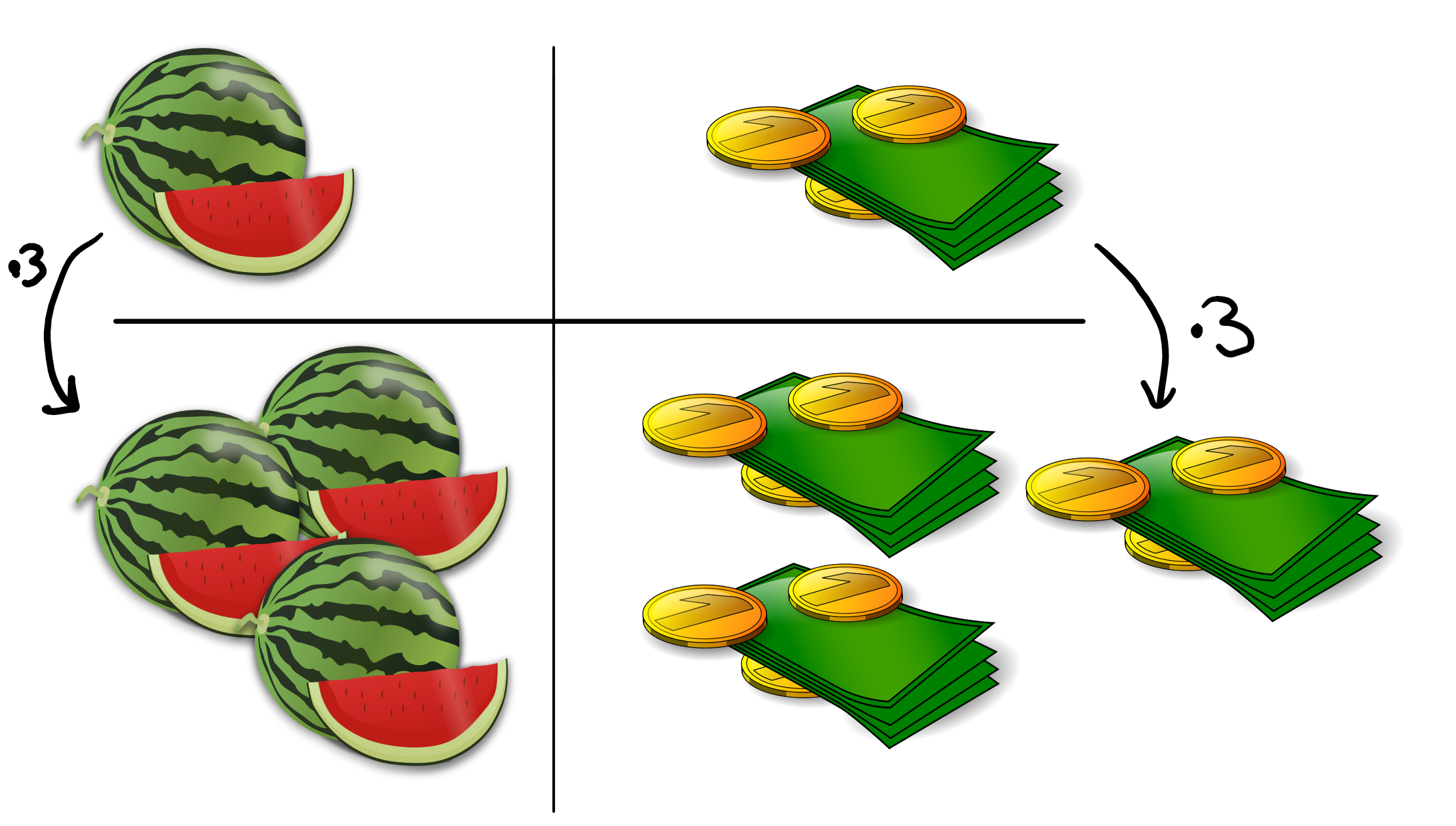
Damit du von Proportionalität sprechen kannst, brauchst du immer erstmal zwei "Größen" oder einfacher gesagt: zwei Dinge, die du in einen Zusammenhang bringen möchtest.

Eine Anzahl von Wassermelonen und ein Geldbetrag, den du für sie bezahlen musst, zum Beispiel.

Oder eine feste Menge von Kuchen und eine Menge von Personen, die den Kuchen essen und sich fragen, wie groß ihr Kuchenstück sein wird.

Oder aber einen Wurf Hundewelpen und die davon bei dir erzeugte Fröhlichkeit (wenn man Fröhlichkeit denn messen kann)

Diese beiden Größen bringst du dann noch ordentlich in die Form einer Zuordnung, z. B.:

Anzahl Melonen $\mapsto$ Preis in $€$

Und dann brauchst du eine Fragestellung: "Wenn ich eine der beiden Größen verändere, zum Beispiel verdopple, was passiert dann mit der anderen Größe?"

4 direkte Proportionalität

Gehst du in den Laden und hast den festen Willen, all dein Geld für Wassermelonen auszugeben, so führt mehr Geld auch immer zu mehr Wassermelonen.

Sorgt doppelt, dreimal, halb, ⁣ $. . .$ so viel von der einen Sache immer auch dafür, dass du doppelt, dreimal, halb, $. . .$ so viel von der anderen Sache hast, so spricht man von direkter Proportionalität.

Man sagt auch: Die Größen ändern sich im gleichen Verhältnis.

Du denkst dir jetzt vielleicht: Easy, das kann ich ja schon seit der Grundschule!

Dann schau dir doch direkt die nächste Folie an.

5 Wertetabelle direkter Proportionalität

Alexander kramt einen alten Kassenbon hervor. Darauf steht, wie viel er für $12$ Melonen gezahlt hat. Dann schiebt er dir einen Block hin, auf den er bereits eine unvollständige Wertetabelle gezeichnet hat.

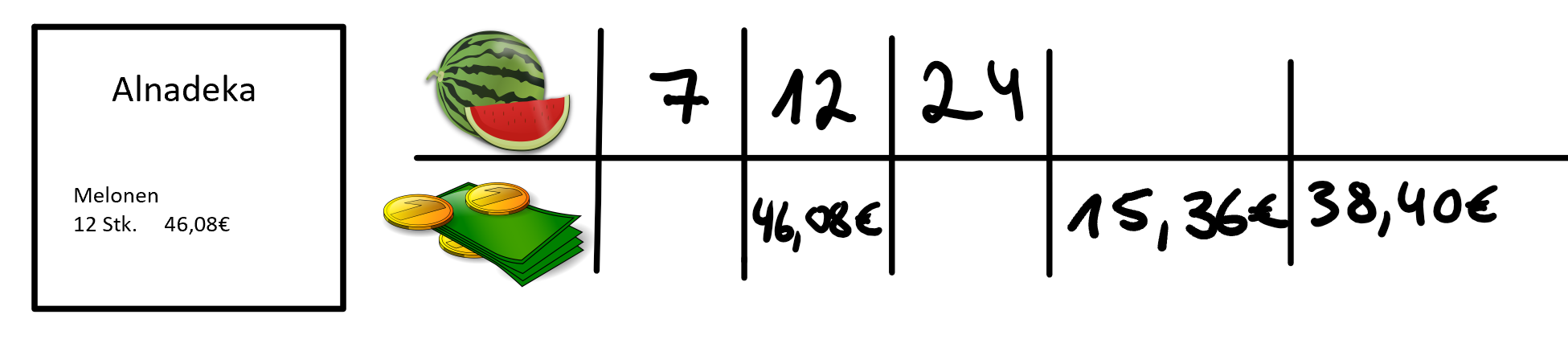
Wie gehst du vor?

Nach etwas Rechnerei schiebst du ihm das Blatt zurück:

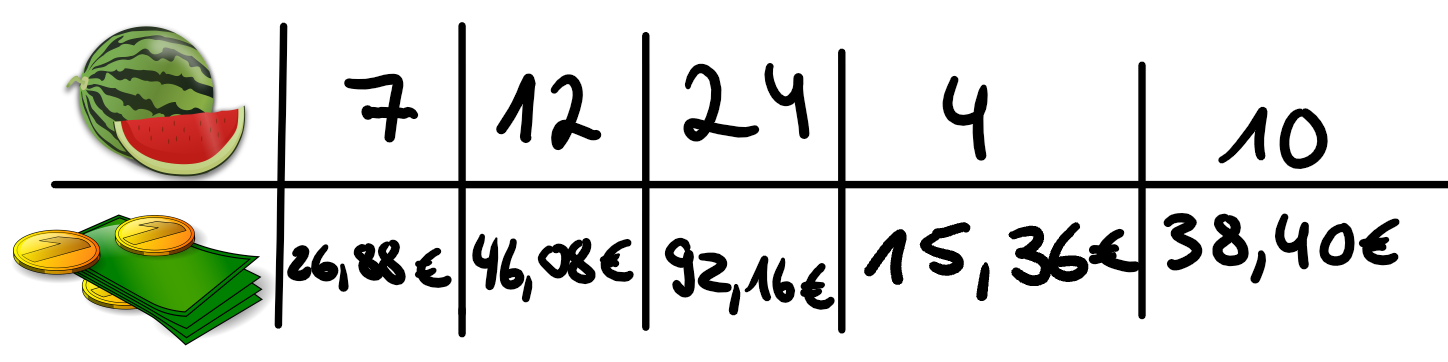
Ist dir aufgefallen, dass bei jedem Wertepaar der Quotient der beiden Größen gleich ist? Dabei ist es egal, ob ich die Melonenzahl durch den Preis dividiere oder umgekehrt.

Melonenanzahl	7	12	24	4	10
Preis in €	26,88	46,08	92,16	15,36	38,40
Melonenanzahl/Preis	$\frac{25}{96}$	$\frac{25}{96}$	$\frac{25}{96}$	$\frac{25}{96}$	$\frac{25}{96}$
Preis/Melonenanzahl	3,84(€)	3,84(€)	3,84(€)	3,84(€)	3,84(€)

6 Quotientengleichheit und Proportionalitätsfaktor

Melonenanzahl	7	12	24	4	10
Preis in €	26,88	46,08	92,16	15,36	38,40
Melonenanzahl/Preis	$\dfrac{25}{96}$	$\dfrac{25}{96}$	$\dfrac{25}{96}$	$\dfrac{25}{96}$	$\dfrac{25}{96}$
Preis/Melonenanzahl	3,84(€)	3,84(€)	3,84(€)	3,84(€)	3,84(€)

Der Wert in der 4. Zeile kommt dir sicher bekannt vor: Es ist der Preis für eine Melone. Der Wert in der 3. Zeile besagt, wie viel Melonen man für $1 €$ bekommt: Etwas mehr als eine viertel Melone.

Dass die Division der Wertepaare das gleiche Ergebnis besitzt, ist bei allen direkt proportionalen Zusammenhängen so. Der Quotient entspricht dabei immer dem zugehörigen Wert der einen Größe für eine "Portion" der anderen Größe.

Die Zuordnung A $\mapsto$ B zweier Mengen zueinander ist genau dann direkt proportional, wenn alle Wertepaare x $\mapsto$ y quotientengleich sind, also $\frac{y}{x}$ für alle Wertepaare den gleichen Wert $k$ liefert. Den Wert $k$ nennt man Proportionalitätsfaktor.

7 Graph der direkten Proportionalität

Erneut schiebt dir Alexander den Block hin und bittet dich darum, die Wertepaare der Zuordnung Melonenanzahl $\mapsto$ Preis in € in ein Koordinatensystem zu malen.

Als du fertig bist, schaust du erst verblüfft, dann nickst du aber und murmelst: "logisch".

Wenn du die Punkte verbindest, entsteht eine Gerade.

Geraden sind die Graphen von Zuordnungen, die gleichmäßig wachsen. Genau das also, was direkt proportionale Größen tun.

Der Proportionalitätsfaktor hat dabei eine ganz besondere Rolle: Er entspricht der Steigung $m$ der Gerade. Klar, denn der Proportionalitätsfaktor gibt ja an, wie viel der anderen Größe man für eine Einheit der ersten Größe benötigt, also wie viel mehr ich für eine Melone mehr zahlen muss.

Dass die Gerade durch den Ursprung verlaufen muss, ist auch klar: Wenn ich nichts von meiner ersten Größe, also keine Melonen, habe, habe ich auch nichts von meiner zweiten Größe, also dem Preis für die Melonen.

Die Graphen von direkt proportionalen Zuordnungen sind Ursprungsgeraden mit der Funktionsgleichung $y = m x$ , wobei die Steigung dem Proportionalitätsfaktor entspricht, also $m = k$ .

8 Übungen

Laden

weitere Aufgaben zur direkten Proportionalität

9 Melone für Alle!

Als dir gerade klar geworden ist, wie nützlich das Bisherige für die ein oder andere (alltägliche) Aufgabe ist, kommt Alexander mit einer aufgeschnittenen Wassermelone zurück.

"Aber was machst du jetzt mit den ganzen Melonen, die du hier herumliegen hast?", fragst du ihn.

"Vorbereitet sein. Stell dir vor, ich hätte nur eine Melone und dann würden unangekündigt $3$ Gäste kommen - das ist noch in Ordnung. Aber wenn ich nur eine Melone hätte und unangekündigt 30 Gäste kommen würden, dann müsste ich die Melonenstücke ja mega klein schneiden."

Langsam hast du den Verdacht, dass Alexander doch eine kleine Macke hat. Aus Höflichkeit nickst du trotzdem und beißt in deine Wassermelone.

10 indirekte Proportionalität

Recht hat Alexander natürlich schon und du fragst dich berechtigterweise, ob auch in dieser Situation ein mathematischer Zusammenhang besteht.

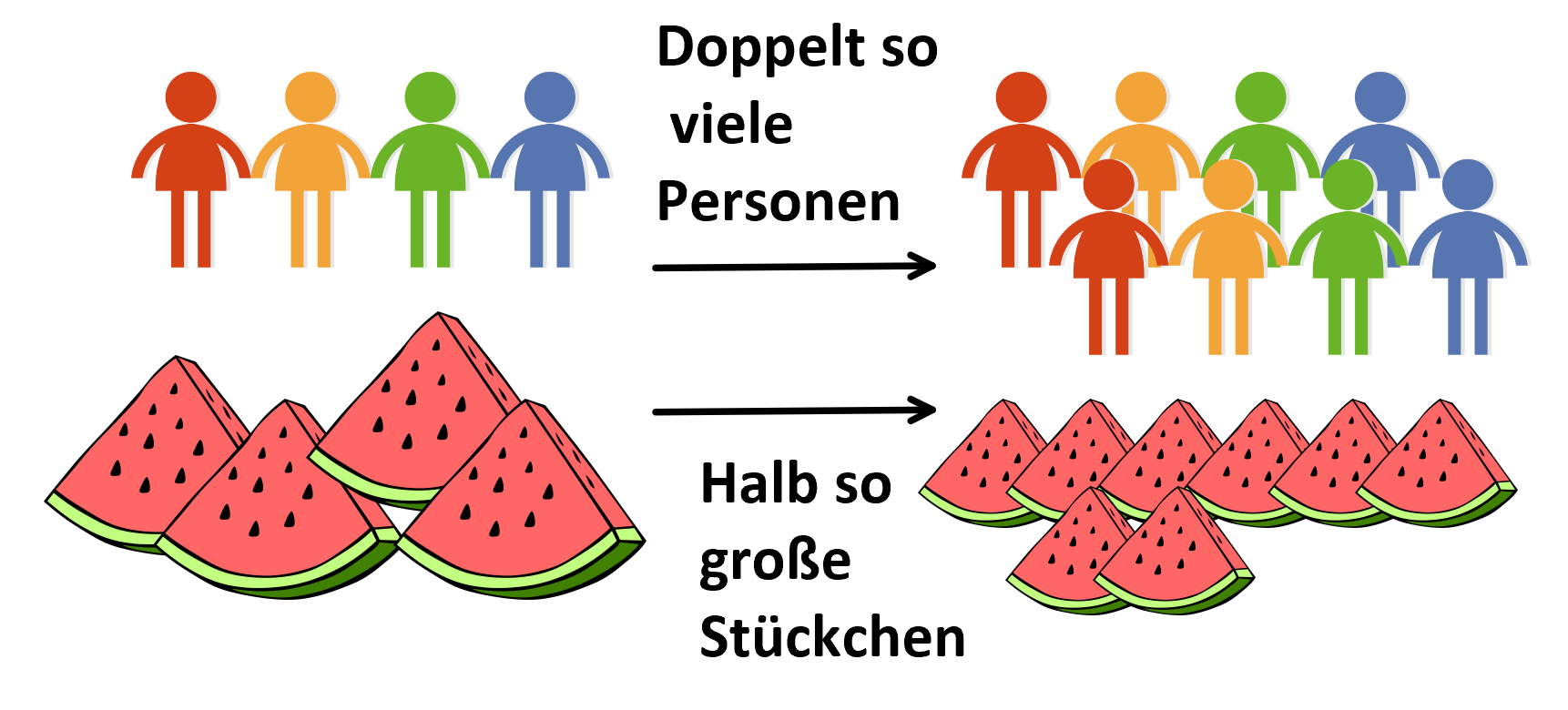
Direkt proportional ist die Situation

Menge der Personen, die eine Melone essen $\mapsto$ Größe der Melonenstücke

auf jeden Fall nicht, denn doppelt so viele Personen bedeuten zwar doppelt so viele Stücke, da aber die Stücke aus einer einzigen Melone geschnitten werden, werden die einzelnen Stücke dabei kleiner. Genauer gesagt sind sie, wenn man ordentlich arbeitet, genau halb so groß.

Sorgt doppelt, dreimal, halb, $. . .$ so viel von der einen Sache dafür, dass du halb, ein drittel, doppelt, $. . .$ so viel von der anderen Sache hast, so spricht man von indirekter Proportionalität.

11 Wertetabelle indirekter Proportionalität

Eine Melone unbekannten Gewichts wurde in Würfel geschnitten, um sie besser wiegen und gerecht an die Personen verteilen zu können. Du siehst eine unvollständige Wertetabelle für die Zuordnung:

Anzahl der Personen $\mapsto$ Gewicht der Melonenportion in Gramm:

Anzahl Personen	4	15	3
Gewicht der Melonenportion (in g)	375			187,5	10	0,1

Hat man das Gesamtgewicht, lässt sich jeder der fehlenden Werte also durch Division mit dem anderen Wert ermitteln:

Anzahl Personen	4	15	3	8	150	15000
Gewicht der Melonenportion (in g)	375	100	500	187,5	10	0,1

Dass jemand leer ausgeht, passiert nie. Allerdings wird die Anzeige der Waage bei steigender Personenzahl immer näher an die $0\;\text{g}$ herankommen $. . .$

12 Produktgleichheit

Hast du bereits übereifrig ausprobiert, ob die Wertepaare wieder quotientengleich sind? Dann hast du festgestellt, dass das nicht der Fall ist. Würde in der Situation ja auch keinen Sinn ergeben: Person pro Gewicht der Melonenportion?

Allerdings hast du vielleicht bei der Berechnung der fehlenden Werte gesehen, dass die $1500\ g$ , also das Gesamtgewicht der Melone, eine entscheidende Rolle spielt:

Multipliziere ich die Anzahl der Personen mit dem Gewicht ihrer jeweiligen Melonenportionen, so erhalte ich bei jedem Wertepaar in der Tabelle $1500\ g$ .

Die Zuordnung A $\mapsto$ B zweier Mengen zueinander ist genau dann indirekt proportional, wenn alle Wertepaare x $\mapsto$ y produktgleich sind, also $x\cdot y$ für alle Wertepaare den gleichen Wert $k$ liefert. Den Wert $k$ nennt man Proportionalitätsfaktor.

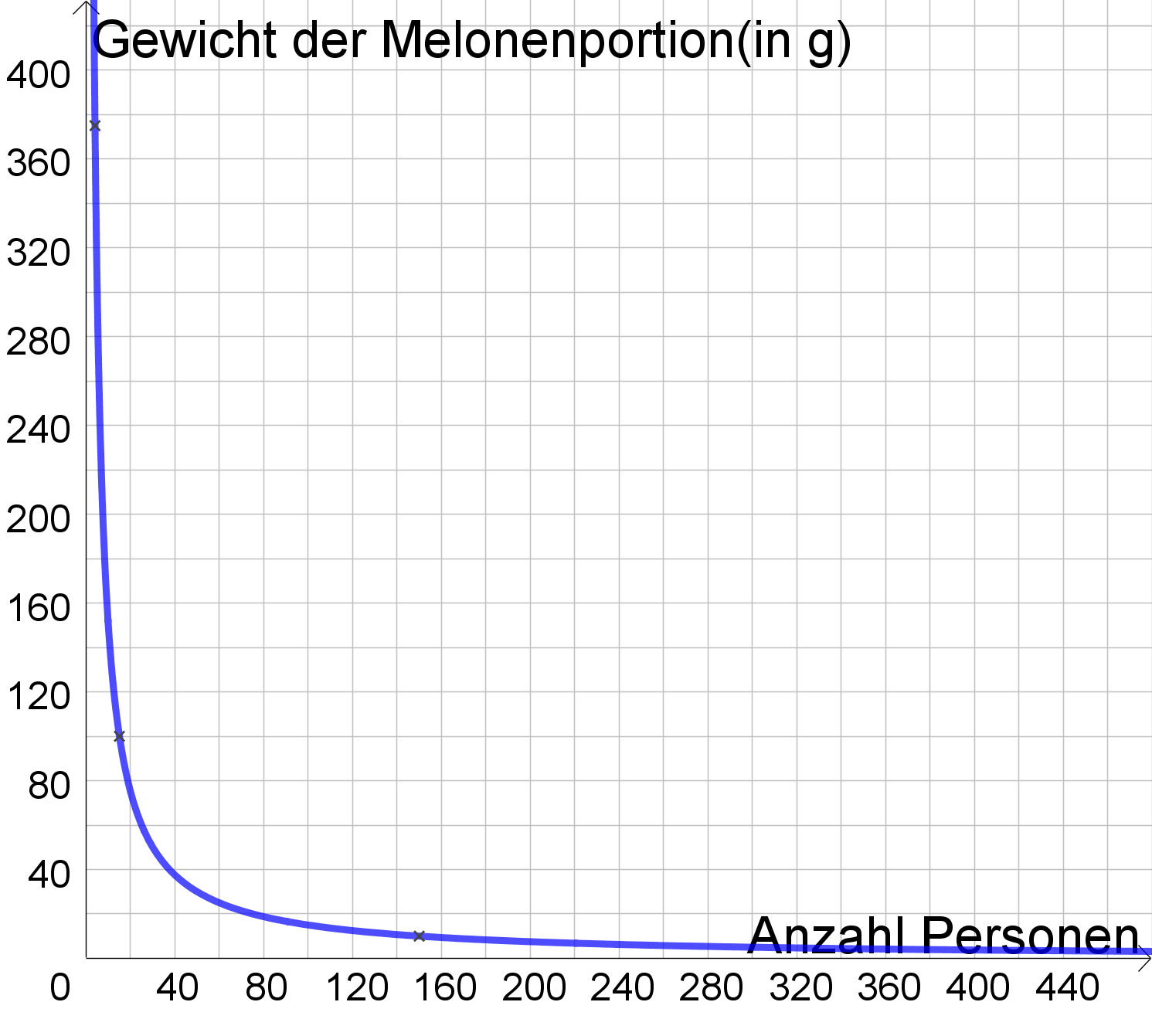
13 Graph der indirekten Proportionalität

Als du selbstständig den Block zu dir ziehst, um deine Vermutung über den Graphen der Zuordnung Anzahl der Personen $\mapsto$ Gewicht der Melonenportion in Gramm zu zeichnen, ist Alexander gerade in sein 17. Stück Wassermelone vertieft.

Du hast die Vermutung, dass es sich um eine Hyperbel handelt, die die Koordinatenachsen als senkrechte beziehungsweise waagerechte Asymptote besitzt und deshalb eine Funktionsgleichung der Form $y=\frac{a}{x}$ hat.

Du setzt eines der Wertepaare ein, um a zu bestimmen:

$\displaystyle 10$	$=$	$\displaystyle \frac{a}{150}$	$\displaystyle \cdot150$
$\displaystyle 1500$	$=$	$\displaystyle a$

Da ist er wieder, der Proportionalitätsfaktor! Egal welches Wertepaar du einsetzt, aufgrund der Produktgleichheit ist $a$ stets $1500\ g$ .

Die Graphen von indirekt proportionalen Zuordnungen sind Hyperbeln mit der Funktionsgleichung $y=\frac{k}{x}$ , wobei $k$ der Proportionalitätsfaktor ist.

14 Übungen

Laden

weitere Aufgaben zur indirekten Proportionalität

15 Alles auf einen Blick

Von proportionalen Zuordnungen spricht man, wenn die beiden Größen gleichermaßen bzw. genau gegengleich abnehmen oder zunehmen. Dabei unterscheidet man direkte und indirekte Proportionalität:

direkte Proportionalität:

$k$ -mal so viel von dem einen sorgt für $k$ -mal so viel von dem anderen, wobei $k$ der Proportionalitätsfaktor ist. Alle Wertepaare $(x ∣ y)$ sind quotientengleich, also $\frac{x}{y}=k$

Der Graph ist eine Ursprungsgerade mit der Funktionsgleichung $y=kx_{ }$

indirekte Proportionalität

$k$ -mal so viel von dem einen sorgt für $\frac{1}{k}$ -mal so viel von dem anderen, wobei $k$ der Proportionalitätsfaktor ist. Alle Wertepaare $(x ∣ y)$ sind produktgleich, also $x\cdot y=k$

Der Graph ist ein Hyperbelast mit der Funktionsgleichung $y=\frac{k}{x}$

Allgemeines

Zwei Größen können zueinander direkt, indirekt oder gar nicht proportional sein.

Aufgrund der Sachsituationen ergeben meistens nur positive Definitions- und Wertemengen Sinn.

16 Kann ich das?

Laden

Gib jeweils an, ob der Zusammenhang direkt oder indirekt proportional ist und beantworte jede Frage mit einem Antwortsatz.

Laden

weitere Aufgaben zu direkter und indirekter Proportionalität

17 Nachhauseweg

Du verabschiedest dich von Alexander und machst dich auf den Nachhauseweg. Ziemlich verrückt, der Herr. Aber gut in Mathe.

Es ist ein warmer Sommertag.

Als du an einem Obsthändler vorbeikommst, bleibst du kurz stehen. Du zückst deinen Geldbeutel und kaufst drei Wassermelonen.

Nur für den Fall, dass du Besuch bekommst.

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?