Springe zum Inhalt oder Footer
SerloDie freie Lernplattform

Gemischte Aufgaben zu Proportionalität und Dreisatz

Lerne mit diesen Übungsaufgaben das Erkennen und Anwenden von Proportionalitäten und das Rechnen mit dem Dreisatz!

  1. 1

    Die folgende Wertetabelle enthält direkt proportionale Wertepaare. Ergänze die fehlenden Werte.

  2. 2

    Bestimme, ob der Zusammenhang direkt oder indirekt proportional ist und beantworte jede Frage mit einem Antwortsatz.

    1. Ein Pkw verbraucht auf 100 km 9,6 Liter Benzin.       Welche Strecke kann er mit einer Tankfüllung von 60 Litern zurücklegen?

    2. Im Baumarkt kosten 40 Linsenkopf-Stahlstifte 0,68 €. Wie viel € würden 250 Stahlstifte des gleichen Typs kosten?

    3. Eine Straße steigt auf 2,4 km Länge um 8,4 m.       Wie viel m würde sie bei gleichbleibender Steigung auf 5 km steigen?

    4. Zur Herstellung einer Garageneinfahrt benötigen drei Pflasterer 7,5 Stunden.       Wie lange würde die Arbeit dauern, wenn 5 Pflasterer eingesetzt werden können?

    5. Ein 6 m² großes Kupferblech mit 4 mm Dicke wiegt 213,6 kg.       Wie viel wiegt ein 3 mm dickes Kupferblech, das eine Fläche von 4 m² hat?

    6. Von einer Bank bekommt ein Tourist 432 Dollar für 400 €.

      Wie viel Dollar hätte er bekommen, wenn er 2250 € umgetauscht hätte?

    7. Ein Verkäufer erhält bei einem monatlichen Umsatz von 45200 € eine Provision von 3164 €. Im nächsten Monat erhöht sich seine Provision um 220,50 €.

      Wie hoch war der Umsatz?

    8. Von 5 Maurern werden 616 m² Mauerwerk in 154 h hergestellt.

      Wie viel Mauerwerk können bei gleicher Leistung 6 Maurer in 160 h herstellen?

    9. Um 1800 m³ Wasser 12 m hoch zu fördern, wird eine Pumpe von 4 kW benötigt.

      Welche Wassermenge könnte von einer 8 kW Pumpe 16 m hoch gefördert werden?

    10. Um 1280 Karosserieteile herzustellen, müssen 4 Stanzen 8 h lang eingesetzt werden.

      Um wie viel Stunden muss die tägliche Arbeitszeit erhöht werden, wenn 2400 Karosserieteile täglich hergestellt werden sollen und zwei Stanzen zusätzlich eingesetzt werden können?

    11. Auf drei automatischen Werkzeugmaschinen lassen sich 150 Metallhülsen in 1 h 15 min herstellen.

      Wie viele Hülsen könnten in 2 h 30 min hergestellt werden, wenn zwei Maschinen zusätzlich zum Einsatz kämen?

      Hülsen

    12. Um eine Decke von 96 m² Fläche einzuschalen, benötigen drei Einschaler 2 Tage bei einer täglichen Arbeitszeit von 8 h.

      Wie viele Tage würden 4 Einschaler benötigen, um eine Decke von 144 m² Fläche einzuschalen, wenn die tägliche Arbeitszeit um 1 h erhöht würde?

    13. In 3 Tagen verbrauchen 6 Dieselmotoren zusammen 2016 Liter Dieselkraftstoff bei einer täglichen Laufzeit von 16 h. Durch Ausweitung der Produktion sollen in Zukunft 8 Motoren eingesetzt werden und die tägliche Laufzeit um 2 h erhöht werden.

      Mit welchem Kraftstoffverbrauch pro Tag muss gerechnet werden?

    14. Die monatliche Stromrechnung für 8 Lampen beträgt bei täglich 8-stündiger Brenndauer 18 €.

      Welcher Betrag ist zu zahlen, wenn 12 Lampen mit gleicher Leistung täglich 6 Stunden brennen?

    15. Zwölf Einschaler haben bei 9 - stündiger Arbeitszeit 390 m² Betonschalung in 7 Tagen hergestellt.

      Wie viele Einschaler sind bei gleicher Leistung einzusetzen, wenn in insgesamt 21 Tagen 2340 m² Betonschalung hergestellt werden müssen, um den Terminplan einzuhalten, und die tägliche Arbeitszeit nur 8 Stunden beträgt?

  3. 3
    strobl-f.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Franz Strobl

    Handelt es sich bei den folgenden Größen um eine direkte oder indirekte Proportionalität:

    1. Die Menge Wasser in einer Mineralwasserflasche und die Zahl der Flaschen, die benötigt werden, um 600 Schulkindern je einen halben Liter Mineralwasser zu bieten.

    2. Die Menge Wasser in einer Mineralwasserflasche und die Zahl der Schulkinder, die mit 400 Flaschen versorgt werden können, dass jeder einen halben Liter erhält.

  4. 4

    Die in den Tabellen dargestellten Größen sind in beiden Fällen proportional. Entscheide, welche Art von Proportionalität jeweils vorliegt und vervollständige die Tabellen. Gib jeweils auch eine Gleichung an, die den Zusammenhang zwischen x und y beschreibt.

    x

    1

    1,8

    2

    4

    y

    3,1

    5,58

    6,2

    17,05

    x

    0,1

    0,2

    0,5

    1

    1,4

    y

    10,5

    5,25

    2,1

    0,75

    0,42

  5. 5

    Zeichne jeweils rechtwinklige Dreiecke mit Hypotenuse c=5cmc = 5 cm und den Katheten a=1,0cma = 1{,}0 cm; 1,5cm1{,}5 cm; 2,5cm2{,}5 cm bzw. 3,0cm3{,}0 cm. Miss in jedem Dreieck den zugehörigen Winkel α\alpha und trage ihn in unten stehende Tabelle ein. Sind Seitenlänge aa und Winkel α\alpha zueinander proportional?

    Seitenlänge a

    1,0

    1,5

    2,0

    2,5

    3,0

    Winkel α\alpha

  6. 6

    Um Bakterien einer Zellkultur abzutöten, werden Antibiotika eingesetzt. In der ersten Stunde wird die Hälfte der Bakterien getötet, in der zweiten Stunde von den noch vorhandenen ein Drittel und in der dritten Stunde von den noch vorhandenen ein Viertel.

    Berechne den Bruchteil der Bakterien, die dann noch vorhanden sind. Gib diesen Bruchteil wie zum Beispiel "4/5" in das Eingabefeld ein.


  7. 7
    strobl-f.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Franz Strobl

    In ein Schwimmbecken gelangen durch 6 gleiche Zuleitungen in fünf Stunden insgesamt 600 m3\text{m}^3 Wasser. Berechne, wie lange es dauert, das ganze Becken (1000 m3\text{m}^3) über nur 4 Zuleitungen zu füllen.

    h
  8. 8

    Wie viele Quadrate zu je 2,5 cm Seitenlänge ergeben einen Quadratmeter?


  9. 9

    Eine Spiralfeder gehorcht dem Hooke’schen Gesetz. Peter hat in einer Schülerübung mit einer Spiralfeder folgende Messwerte notiert.

    F (N)

    0,5

    1,0

    1,5

    2,0

    2,5

    s (cm)

    4,0

    8,1

    11,9

    16,1

    19,9

    1. Überlege dir einen geeigneten Maßstab und stelle die Messwerte graphisch dar.

    2. Gib eine Gleichung an, die den Zusammenhang zwischen Kraft FF und Dehnung ss der verwendeten Feder beschreibt.

    3. „Wenn wir an die Feder ein Massestück von 2 kg2\ kg hängen, verlängert sie sich um ca. 1,6 m1{,}6\ m“, behauptet Peter. Beschreibe, wie er den Wert für die Verlängerung ermittelt haben könnte. Stimmst du seiner Aussage zu?

  10. 10

    Bei Wandverkleidungen werden häufig Profilbretter verwendet. Der im Handel angebotene Preis pro Quadratmeter bezieht sich aber auf die Fläche der Bretter und nicht auf die zusammengesteckten Bretter der zu bedeckenden Wandfläche. Es ist davon auszugehen, dass 1 m21\ m^2 Bretter nur 0,9 m20{,}9\ m^2 Wandfläche bedeckt.

    1. Es sollen 12,4 m212{,}4\ m^2 Wand verkleidet werden. Wie viel im Handel angebotene Quadratmeter Profilbretter müssen mindestens erworben werden?

      m²

    2. Ein Brett ist 3,40 m3{,}40\ m lang und 121 mm121\ mm breit. Wie viele Quadratmeter können mit diesem Brett tatsächlich bedeckt werden? Wie viele solcher Bretter braucht man mindestens für 1 m21\ m^2 Wandfläche?

    3. Im Prospekt wird der Quadratmeter Profilbretter zu 4,55 €4{,}55\ € angeboten. Wie hoch ist der Preis pro Quadratmeter Wandfläche? Reichen 75 €75\ € für eine Wandfläche von 13,5 m213{,}5\ m^2 aus?

  11. 11

    Ein rechteckiges Grundstück wird vermessen und die Länge auf 83,5 m83{,}5\ m und die Breite auf 42 m42\ m festgelegt.

    1. Welchen Flächeninhalt besitzt das Grundstück?

      m²

    2. Ein Käufer bietet für das Grundstück 250000 €250000\ €. Von welchem Preis pro Quadratmeter geht der Käufer aus? (auf Euro genau).

      €/m²

    3. Der Käufer will auf dem Grundstück ein Hotel einrichten. Die örtlichen Bauvorschriften besagen, dass höchstens ein Drittel des Grundstücks bebaut werden darf. Welche Grundfläche hat das Hotel, wenn der Käufer das Höchstmaß dafür sogar um 200 m2200\ m^2 unterschreitet.

      m²
  12. 12

    Bei einem Hilfsprojekt in Afrika wird Milchpulver, das in Säcken zu je 24 kg24\ kg verpackt ist, in Tüten mit  145 kg1\frac{4}{5}\ kg Inhalt abgefüllt.

    1. Wie viele ganze Tüten können aus zwei Säcken insgesamt abgefüllt werden?

      Tüten

    2. In einer Verteilerstelle für Hilfsgüter befinden sich 2222 dieser Säcke. Durch einen Wasserschaden werden 176 kg176\ kg davon unbrauchbar. Welcher Bruchteil der ursprünglichen Menge kann jetzt noch verwendet werden?


    3. Bei einem der Säcke ist durch ein Loch 215\frac2{15} des Inhalts verloren gegangen. Wie viele ganze Tüten kann man von dem Rest des Sackinhalts noch füllen?

      Tüten

    4. Der LKW der Hilfsorganisation, der die Säcke brachte, war um 04:40 Uhr gestartet, hatte um 07:25 Uhr eine Pause von  1251\frac25 Stunden eingelegt, musste wegen einer Reifenpanne um 09:40 Uhr nochmals die Fahrt für  111121\frac{11}{12} Stunden unterbrechen und kam schließlich um 12:25 Uhr bei der Verteilerstelle an.

  13. 13
    Image Title

    Nach dieser Abbildung der Nationalflagge von Benin in Afrika soll eine Fahne aus Tuch gefertigt werden, die 5 m5\ m breit und 3 m3\ m hoch ist.

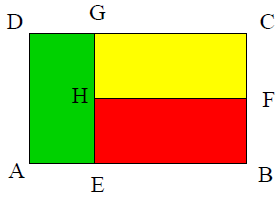
    1. In einer Fabrik wird sie so genäht, dass das Rechteck AEGDAEGD  25\frac25 der Fahnenfläche einnimmt. Die beiden anderen Rechtecke sind gleich groß. Berechne die Stoffmenge für jedes Rechteck in Quadratmetern.

    2. Eine andere Fabrik näht die Fahne so, dass alle drei inneren Rechtecke gleich groß sind.

      Berechne Breite und Höhe jedes dieser Rechtecke in Metern. Runde auf Zentimeter genau.

    3. In einer dritten Fabrik wird die Fahne so genäht, dass die Rechtecke AEGDAEGD und EBFHEBFH zusammen genauso groß sind wie das Rechteck HFCGHFCG. Ordne den Flächeninhalt dieser drei Rechtecke der Größe nach.

  14. 14

    Es gibt viele Zahlenpaare positiver Zahlen, deren Produktwert 0,640{,}64 beträgt.

    1. Gib 1010 solche Zahlenpaare an.

    2. Ermittle das Zahlenpaar, das den kleinsten Summenwert besitzt.


Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?