Die vom Funktionsgraphen und einem Intervall auf der x-Achse eingeschlossene Fläche lässt sich näherungsweise als Ober- bzw. Untersumme bestimmen. Zudem lässt sich das Integral als Grenzwert von Ober- bzw. Untersummen auffassen (s. unten).
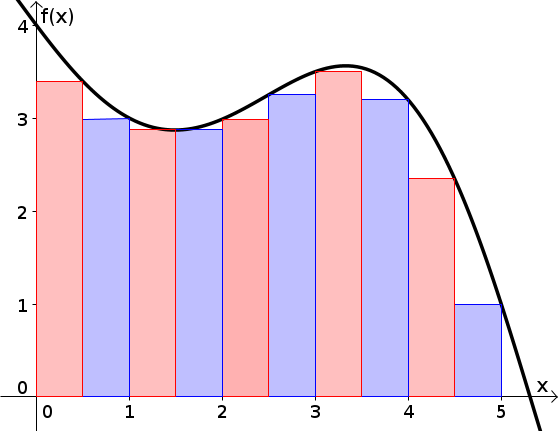
Untersumme der Funktion . Die Stützstellen haben den Abstand
Gegeben sei eine stetige Funktion . Man setzt zunächst voraus, dass die Funktion im betrachteten Intervall nicht ihr Vorzeichen wechselt, also entweder nur positive oder nur negative Werte annimmt.
Ein Beispiel sei folgender Funktionsgraph; gesucht ist die rot markierte Fläche.
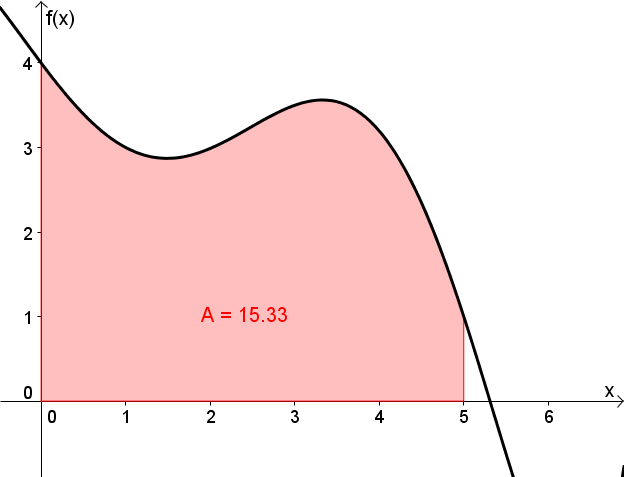
Man erhält eine grobe Näherung der Fläche, wenn man das betrachtete Intervall in Teilintervalle zerlegt.
In jedem dieser Teilintervalle lässt sich die Funktion durch ein Rechteck annähern.
Bei der Obersumme wählt man den größten Funktionswert des betrachteten Teilintervalls als höchsten Punkt des Rechtecks.
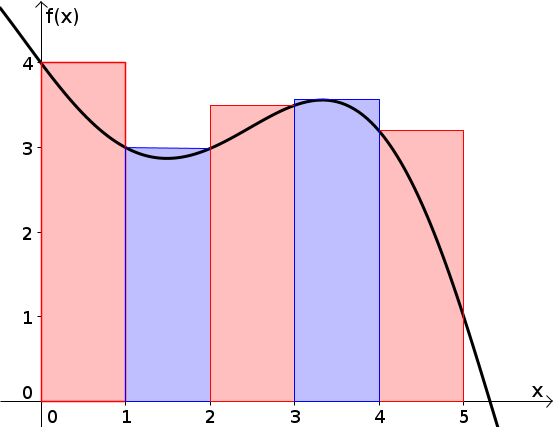
Bei der Untersumme wählt man entsprechend den minimalen Funktionswert.
Die rechte Abbildung zeigt die gleiche Fläche, wie oben. Das Intervall wurde in Teilintervalle der Länge zerteilt und die Obersumme gebildet. Die berechnete Fläche wird also etwas größer sein als die tatsächliche Fläche.
Sollte eines der Rechtecke aufgrund von negativen Funktionswerten unterhalb der x-Achse verlaufen, muss diese mit negativem Vorzeichen in die Berechnung eingehen. Man betrachtet nämlich orientierte Flächen.

Man bezeichnet die Länge der Teilintervalle als Feinheit der Zerlegung. Feinheit bedeutet beispielsweise, dass jedes Intervall die Länge hat (natürlich in x-Richtung).
Je kleiner man die Länge der Teilintervalle wählt, desto genauer ist die Approximation.
Die rechte Abbildung zeigt die Untersumme der Funktion von oben, diesmal mit einer Feinheit von .
Man kann beweisen, dass sich sowohl Ober- als auch Untersumme für eine Feinheit, die gegen läuft, dem exakten Flächeninhalt annähern. Diesen Grenzwert definiert man als Integral.
In Formeln bedeutet das für die Obersumme und die Untersumme , wobei die Feinheit ist, und das Intervall betrachtet wird, dass:
Video zur Unter- und Obersumme
Laden
Die Ungenauigkeit dieser Berechnung
Im unteren Applet kannst du von verschiedenen Funktionen im Intervall die Obersumme berechnen lassen. Am Schieberegler lässt sich die Feinheit einstellen und darunter wird der exakte Wert mit dem Wert der Obersumme verglichen.
Die Ungenauigkeit der Obersumme kann je nach Funktion beliebig klein oder groß sein.
Beispielaufgabe
Berechne die Obersumme von über dem Intervall mit Feinheit und gib die Abweichung von an. Für welche Feinheit ist der Unterschied kleiner als ?
Lösungsskizze
Wenn Feinheit und vorgegebene Intervalllänge übereinstimmen, erhält man ein einziges Teilintervall, dessen Länge der Länge des Ausgangsintervalls entspricht.
Hier ergibt sich das Intervall als Teilintervall der Länge . Aus der Monotonie der Funktion erhält man, dass an der Stelle der maximale Funktionswert des Intervalls angenommen wird.
Für die Obersumme gilt somit: .
Für das Integral gilt hingegen: .
Somit ergibt sich eine absolute Abweichung von .
Zur Berechnung der Feinheit:
Sei für die Feinheit der Zerlegung. Somit ist die Länge aller Teilintervalle . Dann nimmt die Funktion am rechten Rand eines jeden Teilintervalls ihren maximalen Funktionswert auf dem Teilintervall an. Somit gilt für die Obersumme: .
Folglich gilt die Abweichung: . Also muss die Feinheit kleiner als sein.
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
